我在知乎上看到一个好的文章,讲述了我题目中的四个标签,所以,特地发出来。
供大家参考。
全导数是多元函数中的一个概念。
我们知道一元函数的情况下,导数就是函数的变化率,从几何意义上看就是:
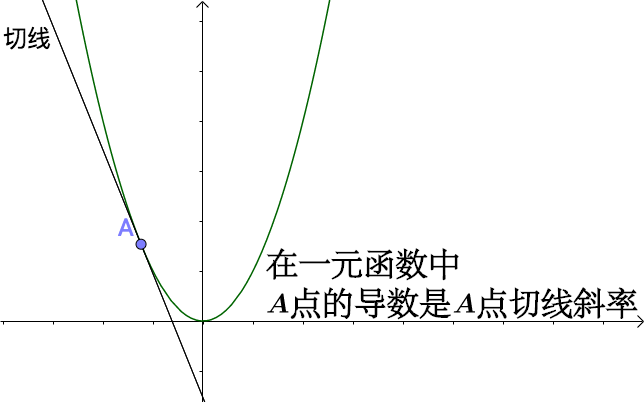
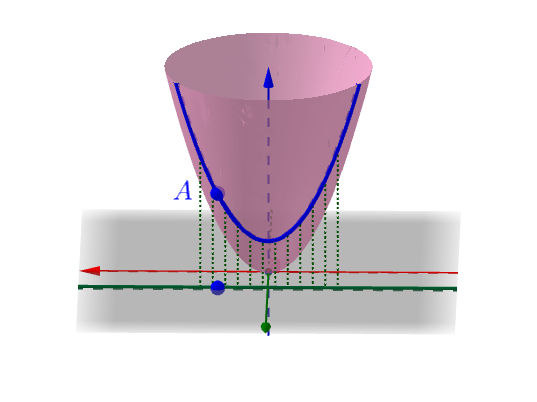
但是在多元的情况下比一元的复杂,下面我用二元函数来举例子(三元我也画不出来),比如这样一个曲面上的一点A :
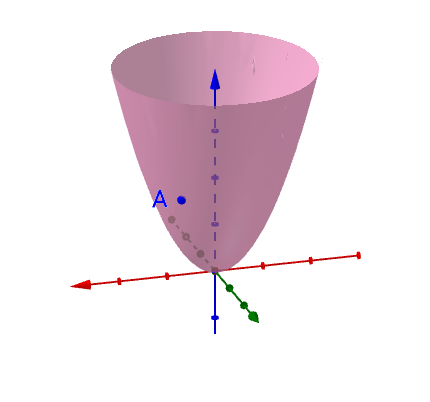
在曲面上可以做无数条过A 点的曲线(图上随便画了三根):
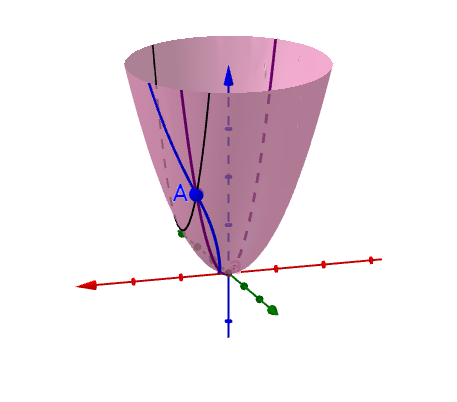
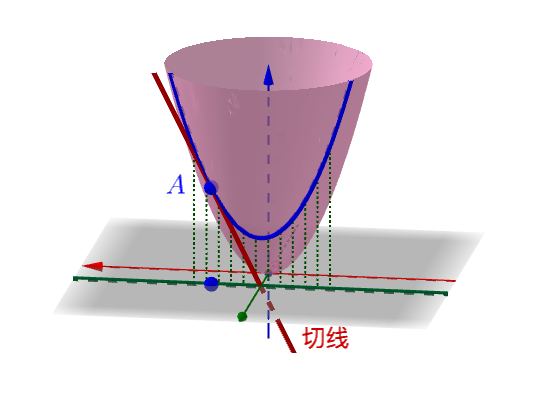
每根曲线都可能可以(也有作不出来的情况,你想想一元的时候也有作不出切线的情况)作一根切线,比如(随便挑了一根切线来画,都画出来太乱了):

全导数的意义:每一根切线都和一个全导数“相关”,A点有无数个全导数。
最精简的回答已经完了,后面我就要讲一些细节了,主要阐述下面两个细节:
方向导数、偏导数是特殊的全导数
每一根切线都和一个全导数“相关”,这个“相关”是什么意思?难道不就是切线的斜率就是全导数吗?顺便说一下,如果所有这些切线共面的话,那么这个平面就是切平面(全微分)
参数方程
为了继续讲下去,我们需要了解下所需要的技术手段:参数方程。
参数方程的用处很多,下面讲解下我们需要了解的部分。
通过参数方程来描述所有的曲线
要描述所有这些曲线,我们就需要一些数学手段,这就是参数方程。
我们来看一下,随便画一条过A 点的曲线:
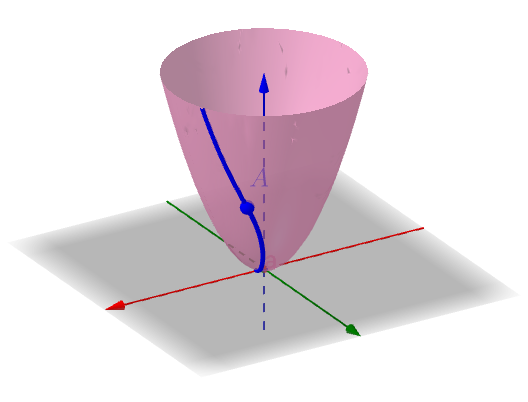
这条曲线也是一个关于x,y 的函数f(x,y) ,因此它与xy 平面上的曲线具有一一对应的关系:

因此我们只需要描述xy 上的曲线就可以达到描述曲面的曲线的目的,这时候就很自然的可以使用参数方程了。
举个具体的例子,对于f(x,y)=x^2+y^2 这个二元函数,函数图像是这样的:
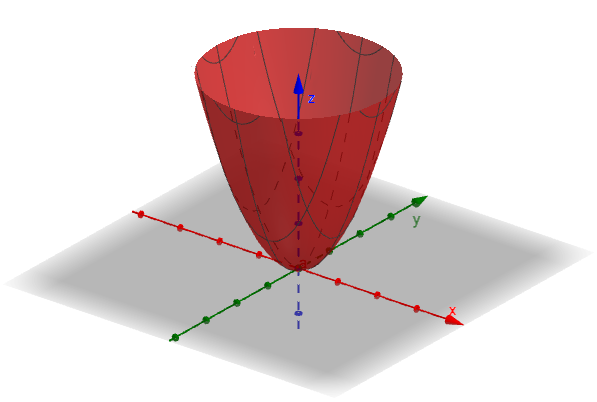
注意此时的x,y 都可以自由改变:
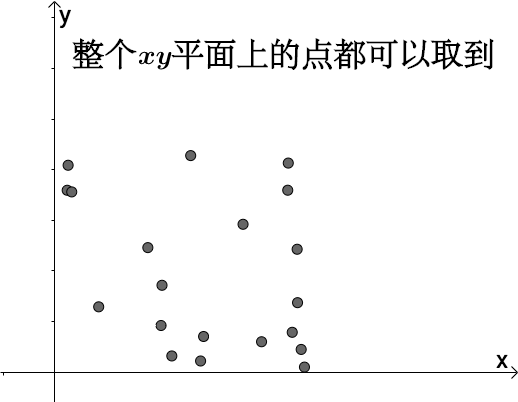
但是如果增加参数方程:
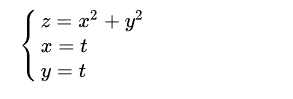
这有什么意义?
此时的 x,y 的变化受到
x = t
y = t 的约束

我们来把这根参数方程决定的直线放到三维空间去:
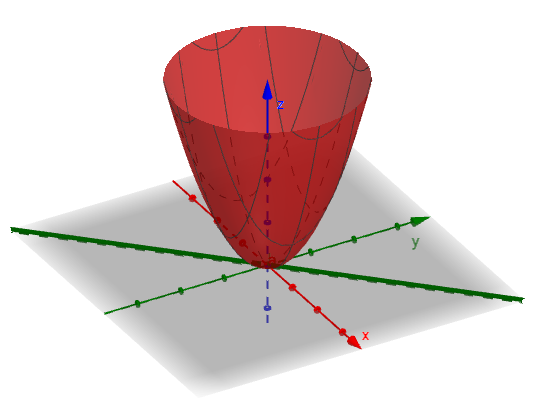
根据之前的描述,这根直线可以决定一根曲面上的曲线:
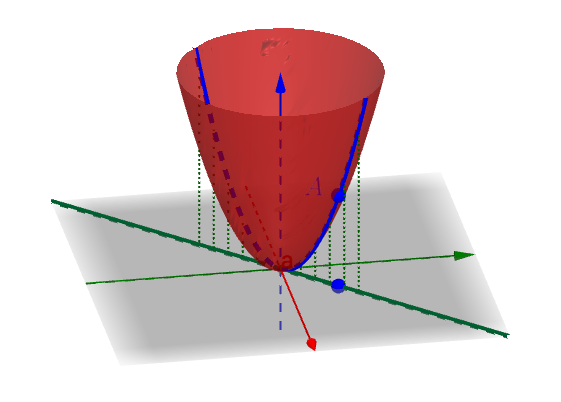
这根曲面上的曲线就是刚才说过的:
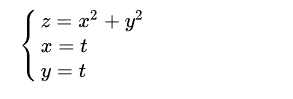
参数方程可以拍扁三维图像
从另外一个角度看,参数方程可以把三维的图像一巴掌拍扁。
什么意思,我们来看看,还是f(x,y)=x^2+y^2 这个二元函数:

增加参数方程约束:
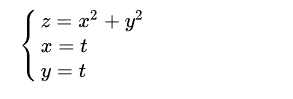
把x,y 代入到z 里面去,可以得到z=2t^2 :
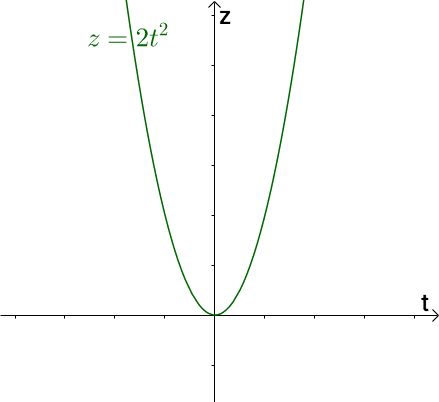
这就好比把xyz 空间的立体图形拍扁到了zt 平面,这个特性在后面会用到,所以在这里先预热下。
偏导数、方向导数、全导数
讲完“所有曲线”之后,我们要来讲这些曲线的切线了,不同的曲线有不同的切线,也就有不同类型的导数。
偏导数
由xy 平面中平行于x 轴或者y 轴的直线决定的曲线:
这根曲线的方程也可以写成参数方程(以平行于x 轴的曲线为例,a 为常数):

偏导数就是这根曲线的切线的斜率:
方向导数
xy 平面不光有平行于坐标轴的直线,还有各种射线,由这些射线决定的曲线:
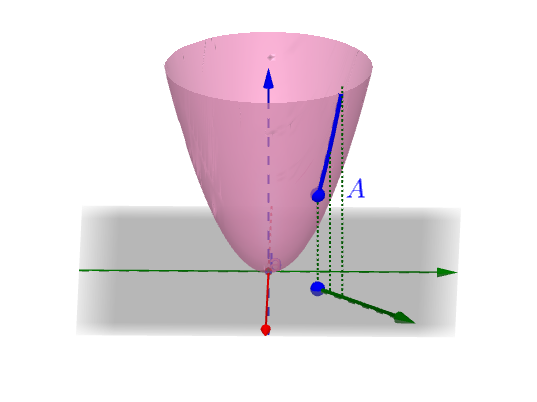
为什么是射线?我们回想一下一元函数中左可导、右可导的概念:
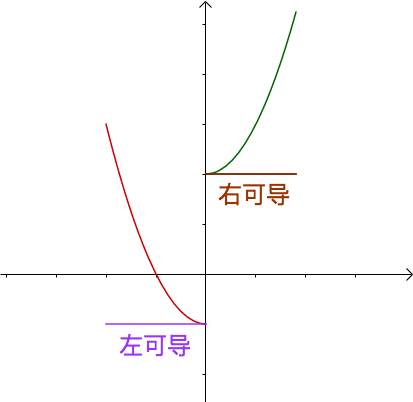
射线可以类比左可导、右可导中的“左”和“右”。
方向导数也就是这根曲线的“左导数”、“右导数”:
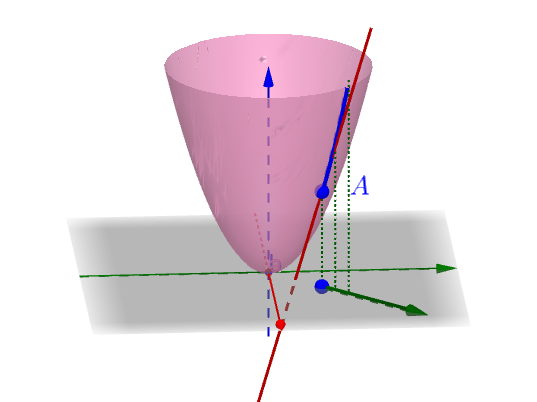
假设A 点的坐标为(x_0,y_0,z_0) ,则该曲线方程的参数方程为
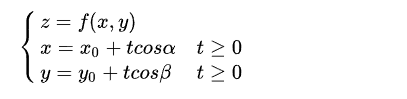
全导数
除了直线射线以外, xy 平面上还有很多不同的曲线,这些曲线总可以写成参数方程的形式:

这些曲线也总能决定曲面上的曲线,比如我之前画过的图:
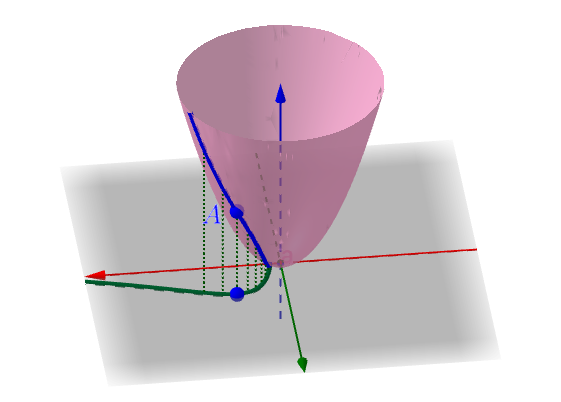
曲线的参数方程可以写成:

讲到这让我先总结一下:
过点A 可以做无数条曲线
所有这些曲线都可以写成参数方程的形式
偏导数、方向导数、全导数由不同的曲线所决定
偏导数、方向导数其实是特殊的全导数总结了之后我要继续讲全导数最重要的一个问题,那就是:
一般来说(除了偏导、方向导数,下面说的全导全部指除了偏导和方向导数之外的),全导数不是这根曲线的切线的斜率。
为什么“偏导数”、“方向导数”都是切线的斜率,而全导数不是呢?
拍扁并且变形了
之前说过参数有拍扁的特性。
在xyz 平面中,偏导数的曲线其实位于平行于x 轴的平面上:
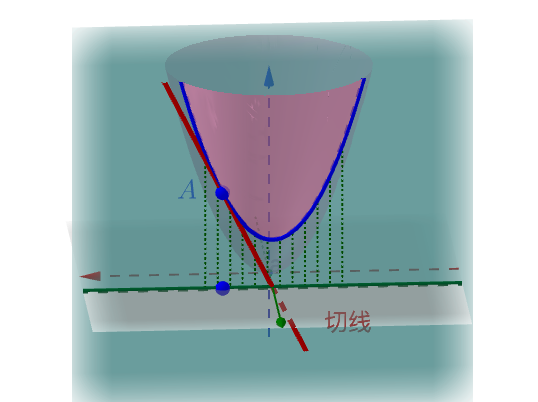
拍扁到zt 平面:
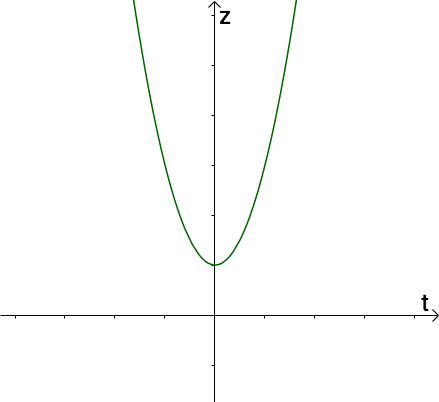
本身也就是平面,拍扁之后也不会发生变形。
因为偏导是特殊的全导,所以我们可以认为偏导就是dz / dt ,也就是 zt 平面上切线的斜率:
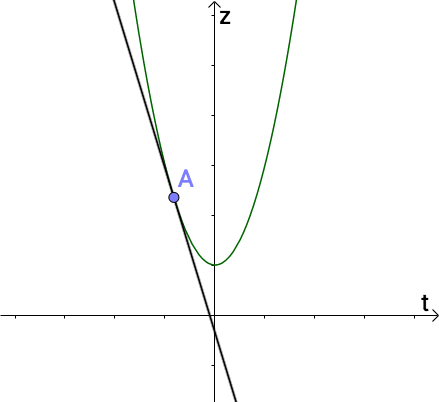
因为没有拍扁过程中没有发生变形,所以zt 平面上切线也就是xyz 空间中的切线。
同样的道理,方向导数的曲线也是位于平面之中的,所以拍扁过程也不会变形。
但是,普通的全导(也就是曲线不在平面中的),拍扁的过程中会变形,比如说还是我之前举的决定全导数的曲线:
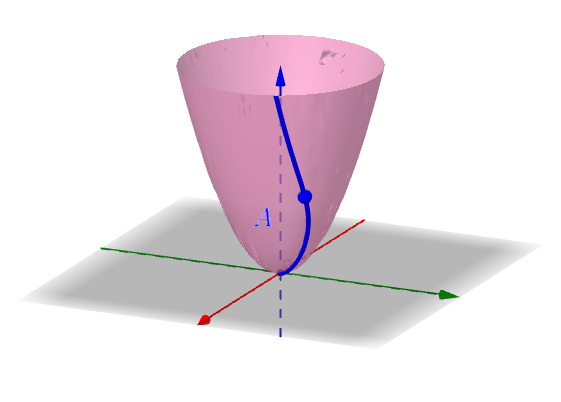
把它拍扁到zt 平面中去:

不得不说看起来还是有那么一点像,不过已经严重变形了。所以全导 dz / dt 在 zt 平面上还是切线的斜率:
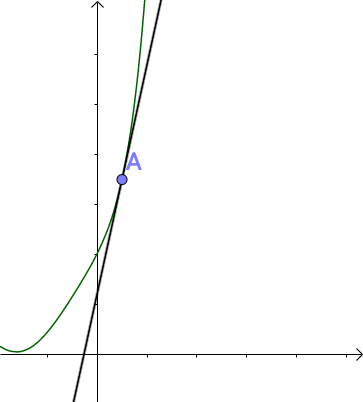
但因为变形,已经不是xyz 空间中的切线(实际上要是还原回去的话是一条曲线)。
至于xyz 空间中切线的斜率要怎么求,就是切向量的问题了.
梯度
函数f(x,y) 的A 点在这个方向上也是有切线的,其切线的斜率就是方向导数:

很显然,A 点不止一个方向,而是360度都有方向:
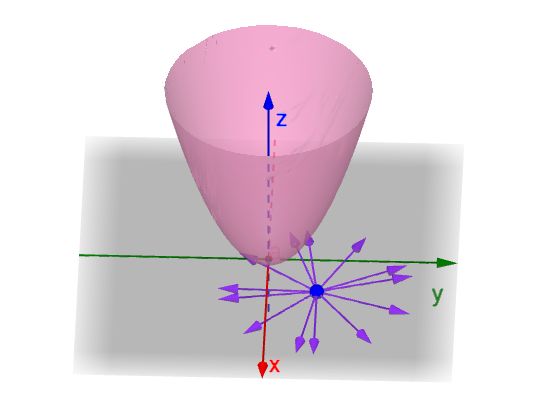
每个方向都是有方向导数的:

这就引出了梯度的定义:
梯度:是一个矢量,其方向上的方向导数最大,其大小正好是此最大方向导数。定义出来了,并不复杂,但对于我而言这才是开始,因为我还有两个疑问:
为什么所有方向导数中会存在并且只存在一个最大值?而不是有多个最大值、或者说没有最大值?
这个最大值在哪个方向取得?值是多少?为什么所有方向导数中会存在并且只存在一个最大值?
其实我最困惑的是梯度的存在性,你说有这么多方向导数,有最大值我觉得还好理解,为什么偏偏只有一个?
我们来看一个显而易见的物理现象:

光滑的、笔直的玻璃上的水滴,一定会沿着玻璃滑下来,(理想情况下)滑下来的方向就是玻璃最陡峭的地方。对于笔直的平面玻璃而言,这个滑下来的方向是只有一个。
说这个干什么?我们回头来看看梯度的数学定义,并且画一下重点:

具有一阶连续偏导数,意味着可微。可微意味着函数f(x,y) 在各个方向的切线都在同一个平面上,也就是切平面:
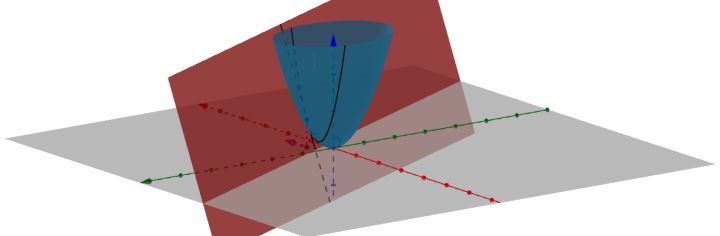
所有的切线都在一个平面上,就好像刚才我说过的光滑的笔直玻璃上,某一点一定有且只有一个(梯度为0的情况除外,可以自己想想为什么?)最陡峭的地方(因为方向导数是切线的斜率,方向导数最大也就意味着最陡峭)。
这就解决了我对于“为什么所有方向导数中会存在并且只存在一个最大值”的疑问。
注意,因为这里举的例子是水滴往下滑,所以要说多说明一下,往下滑是梯度的反方向。因为梯度指的是增长最快的方向,而往下滑是减少最快的方向。
这个最大值在哪个方向取得?值是多少?
这个最大值的方向我们就取名为梯度方向。
最大方向导数的值是多少这个问题,我没有找到特别直观的方法来说明。我也不想给出计算步骤,要不看起来和数学书也没啥区别。大家自己去查找计算过程吧。
方向导数与梯度的关系
方向导数与梯度的关系,我在这里给大家一个直观的操作感受。
先说明一下,下图的矢量表示f(x,y) 在A 点处的梯度,切线是梯度方向的切线。因为我把梯度画在了A 点处,所以我画了一个辅助平面,这个平面和xy 平面平行:
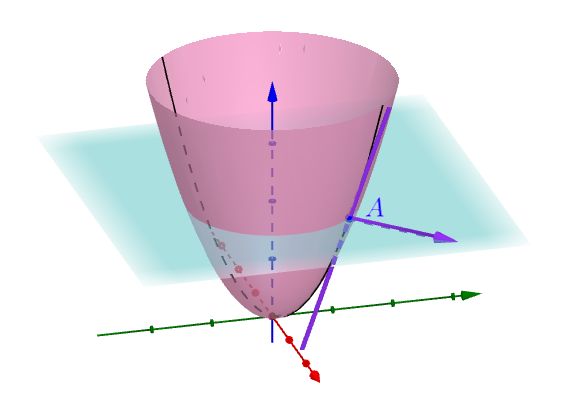
为了方便观察,我把切平面也画出来了,切平面和之前的辅助平面有一根交线,这根交线很明显平行于xy 平面:

我增加切平面、平行于xy 的平面以及两者的交线,都是为了方便有个参照物,看出切线的陡峭的程度。
然后我们来观察不同方向的切线和梯度方向的切线的关系(绿色是梯度以外的方向,它和梯度成 θ 夹角):

自己动手操作以下,就很容易观察出为什么梯度是最陡峭的方向,以及 θ 对方向导数大小的影响:

总结
方向导数是各个方向上的导数
偏导数连续才有梯度存在
梯度的方向是方向导数中取到最大值的方向,梯度的值是方向导数的最大值一直沿着梯度相反的方向就可以到达谷底(原理和弹珠从高处滚落最后会滚进最低处一样)

机器学习中的梯度下降
什么是梯度
在回答什么是梯度之前,要先回答什么是导数,偏导数,方向导数
什么是导数
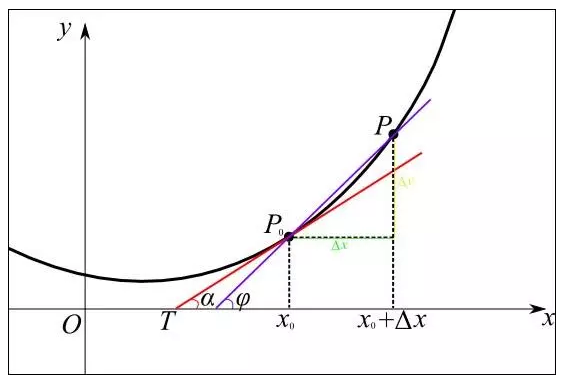
定义:
当函数y=f(x)的自变量x在一点x0上产生一个增量Δx时,函数输出值的增量Δy与自变量增量Δx的比值在Δx趋于0时的极限a如果存在,a即为在x0处的导数,记作f’(x0)或df(x0)/dx。
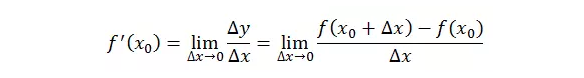
什么是偏导数
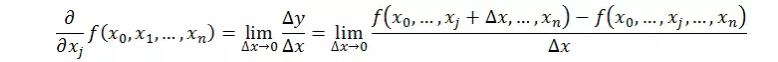
可以看到,导数与偏导数本质是一致的,都是当自变量的变化量趋于0时,函数值的变化量与自变量变化量比值的极限。
什么是方向导数

在前面导数和偏导数的定义中,均是沿坐标轴讨论函数的变化率。那么当我们讨论函数沿任意方向的变化率时,也就引出了方向导数的定义,即:某一点在某一趋近方向上的导数值
什么是梯度
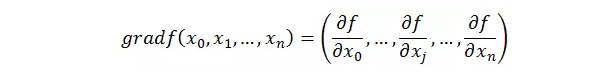
梯度的提出只为回答一个问题:
函数在变量空间的某一点处,沿着哪一个方向有最大的变化率?
函数在某一点的梯度是这样一个向量,它的方向与取得最大方向导数的方向一致,而它的模为方向导数的最大值。
这里注意三点:
1)梯度是一个向量,即有方向有大小;
2)梯度的方向是最大方向导数的方向;
3)梯度的值是最大方向导数的值。什么是梯度下降法
既然在变量空间的某一点处,函数沿梯度方向具有最大的变化率,那么在优化目标函数的时候,自然是沿着负梯度方向去减小函数值,以此达到我们的优化目标。
如何沿着负梯度方向减小函数值呢?既然梯度是偏导数的集合,那么我们在每个变量轴上减小对应变量值即可。
梯度下降法可以描述如下:

以上就是梯度下降法的由来,大部分的机器学习任务,都可以利用Gradient Descent来进行优化。