在这一篇中,我会讲述神经网络的全部内容,包括数学推导还有思维抽象,虽然我之前也写过类似的文章,但是,之前的文章都太浅了,所以,我想将资源进行整合。
在这篇 blog 中你会了解什么是前向传播,什么是反向传播,以及他们的数学推导。
神经网络的前世
感知器是上世纪 50 年代,Frank Rosenblatt 受 Warren McCulloch 和 Walter Pitts 工作的启发,所提出的概念。如今,其他的人工神经元模型更常用,最广泛的是 sigmoid 神经元。现在先让我们看看感知器模型,它将帮助我们了解为什么 sigmoid 神经元更受欢迎。
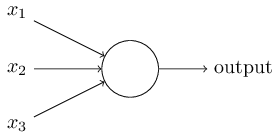
感知器如何工作呢?一个感知器有多个二进制输入,x1,x2,…,并只有一个二进制的输出:
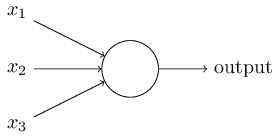
这个例子中,感知器有三个输入,x1,x2,x3。通常输入数目由需要而定。Rosenblatt 给每一个输入引入一个权重,w1,w2,…,在输出增加一个阈值,超过阈值时才会输出 1,以下为输出与输入的关系:
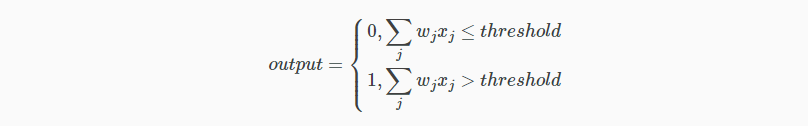
这个简单的公式就是感知器的工作原理!
下面给出一个简单的模型,虽然不是实际例子,但易于理解。假设周末即将来临,你听说自己所在的城市会举办奶酪节。你太喜欢奶酪了,但还是得考虑一下周末的天气情况。你将根据下面三个因素来做决定:
天气怎样?
你的女朋友和你一起去吗?
节日举办地驾车方便吗?将这三种因素量化成二进制数 x1,x2,x3。比如如果天气好,则 x1=1,否则为 x1=0。其他三种因素同理。现在假设你太喜欢奶酪了,以至于女朋友和交通不遍都不太影响你,但你又怕糟糕的天气弄脏衣服。我们可以将感知器设计为:天气权重w1=6,女朋友权重 w2=2 和交通状况权重 w3=2。可以看到天气占了很大的权重。最后将感知器阈值设为 5 便得到了我们需要的决策模型。一旦天气不好,感知器输出为 0,天气晴朗就输出 1。而女朋友同去与否和交通状况都没法影响感知器输出。
通过改变加权系数和阈值,便能得到不同的决策系统。比如将阈值调整为 3,这样女朋友就对你很重要啦,她要是想去,天气再糟你也得跟着一起受罪。
虽然感知器并不是人类决策系统的完整模型,但其能对各种条件做加权。而且似乎越复杂的网路越能做出微妙的决策:
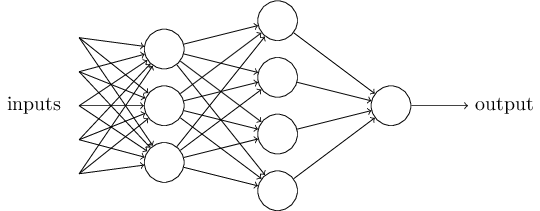
在这个网络中,第一列感知器 - 我们也称作感知器第一层,只是简单地对输入做加权。而第二层感知器则对第一层决策的结果再一步加权,做出更复杂更抽象的决定。同样还可以增加神经网络的层数来作出更复杂的决定。
顺便提一句,上述定义中,感知器只有一个输出,但是上述网络似乎有多个输出。事实上,这仍然是单输出系统,只是单个输出连接到了下一层的多个输入而已。
让我们来简化一下感知器的数学表达式,原来的判断条件 ∑jwjxj>threshold 略显累赘。首先用点积形式简化,记 w⋅x≡∑jwjxj,其中 w 是权重向量,x 是输入向量。然后将阈值移到不等式左边,并用偏移的概念取代它,记 b≡−threshold。感知器规则可重写如下:

偏移的概念可用来度量感知器的“兴奋”程度,假如偏移值很大,那么很小的输入就会在输出端反应出来。但若偏移值很小,则说明感知器比较“迟钝”,输入很大时,输出才有变化。接下来的文章中,都会使用偏移而不是阈值的概念。
sigmoid 神经元
自学习的 idea 听起来太棒了。如何为神经网络设计算法呢?假设我们的神经网络全部由感知器构成,输入为手写体数字扫描图的每一个原始像素点。我们希望神经网络能够自调整权重和偏移值,从而能对手写数字准确分类。为了解自学习过程,我们来做一个思想实验,假设我们在权重或偏移做一个小的改变,我们期望输出也会有相应小的变化:
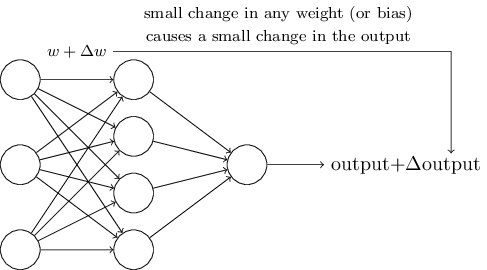
比如神经网络错误地将数字 9 认为为数字 8,我们就可以对参数做微调(可能某个人写的 9 像 8),修正输出,不断重复上述过程,从而使输出符合我们的预期。
实际中,由感知器组成的神经网络并不如所愿。由于感知器的输出不是连续的,0 到 1 是阶跃变化,上述参数的微调往往带来输出的剧烈变化。这下便导致自学习过程完全不可控,有时一点小小的噪声,输出就天壤之变。
针对这个问题,我们可以换用 sigmoid 神经元。sigmoid 神经元和感知器是类似的,但输出是连续且变化缓慢的。这个微小的不同使神经网络算法化成为了可能。
好,让我来描述一下 sigmoid 神经元。其结构和感知器一样:
同样有输入 x1,x2,…。不同是,输入可以取 0 到 1 之间的任何值,比如 0.638。sigmoid 对每一个输入有一个权重,w1,w2,…,以及全局的偏移 b。但是 sigmoid 的输出不再限于 0 和 1,而是
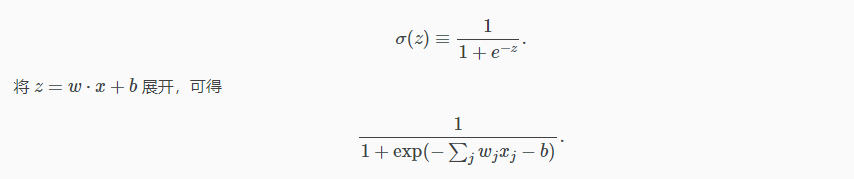
初看上去,sigmoid 神经元似乎与感知器有着天壤之别,其代数表达式也显得晦涩难懂。然而他们之间是有很多相似之处的。
假设当 z≡w⋅x+b 趋向于正无穷,则 e−z≈0 和 σ(z)≈1。换句话说,当输入很大时,sigmoid 神经元的输出趋向于 1,这和感知器是一样的。相反的,当 z≡w⋅x+b 趋向于负无穷,则 e−z→∞,且 σ(z)≈0。这和感知器又是一样的。只有当输入不大时,才会与感知器表现不同。
让我们看一下 sigmoid 函数和阶跃函数的图像:
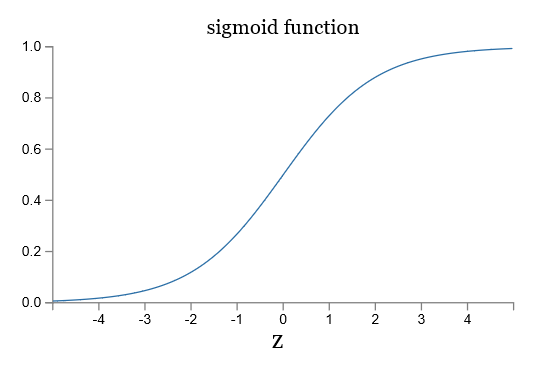
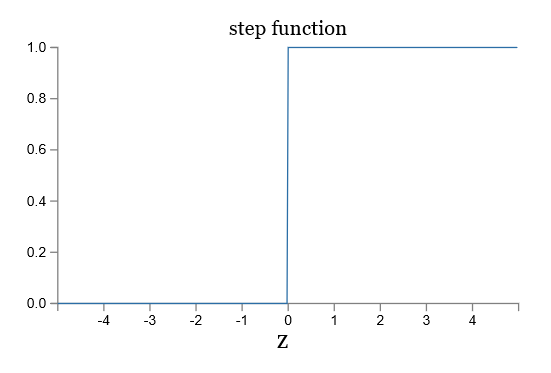
如果 σ 是阶跃函数,那么 sigmoid 神经元就会退化成感知器,也就是说 sigmoid 神经元是平滑了的感知器。函数 σ 的平滑度意味着,权重的微小变化 Δwj 和偏移的微小变化 Δb 会在输出有相应的变化 Δoutput,运用泰勒公式可得:
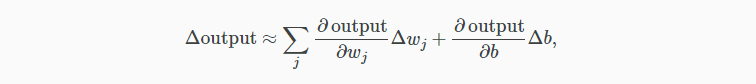
其中,求和是对所有的权重和偏移变化求和。 ∂output/∂wj 是 output 对 wj 的偏导数,∂output/∂b 是 output 对 b 的偏导数。从这个近似表达式可以看出,Δouput 是 Δwj,Δb 的线性函数。比起感知器那种非线性的输出输入关系,线性化便于调试,也有利于算法化。
如何理解 sigmoid 神经元的输出呢?显然最大的不同是 sigmoid 神经元不只输出 0 或 1,而是 0,1 之间所有的实数,比如 0.4 来指出一幅图片是 9 的概率为 40%,60% 的概率不是 9。
我以前的文章
事实上,你根本不用看我以前的文章,因为,以前的文章有很多瑕疵,所以,我才下定决心再来完善一遍。
当然,事物总是善变的,可能不久的将来我又会觉得这篇文章写的不好,这只能证明我又成长了。
参考资料
参考资料有很多,在这里只列出对我这篇文章影响最深的链接。
神经网络的结构
神经网络发展到现在已经有很多变种,包括
convolutional neural network (卷积神经网络)
擅长图像识别
long short-term memory network (长短期记忆网络)
擅长语音识别相关的变种还有很多,但是只有将所有的源头,神经网络学会之后,才能踏入别的领域的殿堂。
所以这一章,我们只会讲解多层感知机(MLP)。
我们会用 MNIST 手写字符来入门,在下一篇中,我会手把手教你如何搭建这个网络。
在此之前,让我们感谢 MNIST 数据库的创始者。现在让我们来聊一聊更细的东西。
什么是神经元,它们又是如何连接的
对于简单神经网络的神经元来说,它只是一个用来装数字的容器,装着从 0 - 1 之间的数据(在这里尤为注意是从 0 - 1)。
MNIST 中每一个数字都是由 28 * 28 个像素点组成的。(下图是 14 * 14 的,请忽略,无论是多大的比例,对于思想都是不影响的)
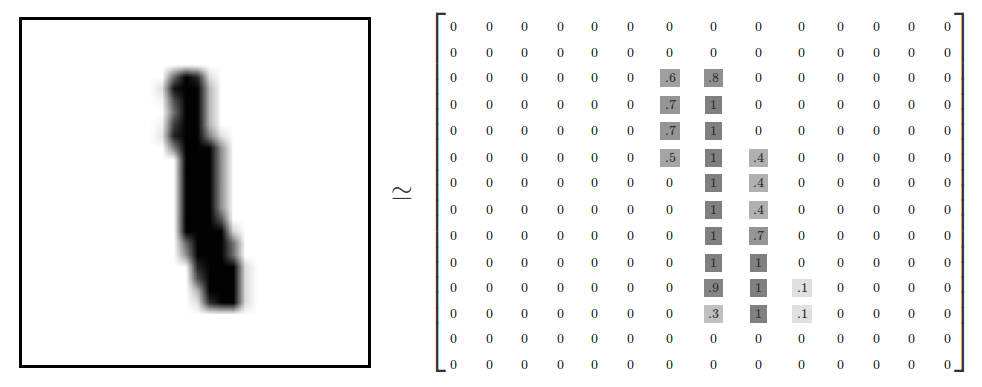
将这个矩形像素拉成 1* 784(28 * 28 = 784),即为 784 个神经元。我们从图中的灰度值可以得到,灰度值越接近 1 ,就越黑,灰度值越接近 0 就越白。(当然,有的图中是越接近 0 就越黑,越接近 1 就越白,这个也无所谓,不影响思想)
而神经元中存储的值就是灰度值。我们将神经元里面装的数成为“激活值”。
所以,这 784 个神经元就组成了我们第一层的神经层。

通过逻辑我们可以很容易的得知,神经网络的最后一层,对应 10 个神经元,分别对应 0 - 9 。同理,最后一层的神经元的激活值也应该在 0 - 1 之间。
神经网络中间还有几层隐藏层,目前我们将它视为黑箱,里面就进行着处理识别数字的具体工作。
在上面的隐藏层中,我们每一层都有 16 个神经元,这些神经元的个数都是随便选的。
神经网络的运作
神经网络上一层的激活值将决定下一层的激活值。所以,神经网络的核心机制正是,一层的激活值是通过怎样的运算,算出下一层的激活值的。
我们第一层有 784 个神经元,这一层的激活值的图案会让下层的激活值缠身某些特殊的图案,进而再让下层产生特殊图案,最终输出选择。
输出层激活值最大的那个神经元就是神经网络的选择。
神经网络为什么分层
为什么分层之后的神经网络就能够辨识出手写字体。中间那那两层究竟是做了什么运算?
我们人脑是如何辨识手写数字的。
我们辨识一个 9 ,我们会注意到上面是一个 0 下面是一个 1。
辨识一个 8 ,上面是一个 0 ,下面是 一个 0.

那计算机是不是也是这样?
我们一共有两个隐藏层,我们希望最后一个隐藏层能够对应上述的部件笔画。即每一个神经元可能对应某一部分,然后最后一层的输出层将这些激活了的笔画进行组合,产生对应的数字。
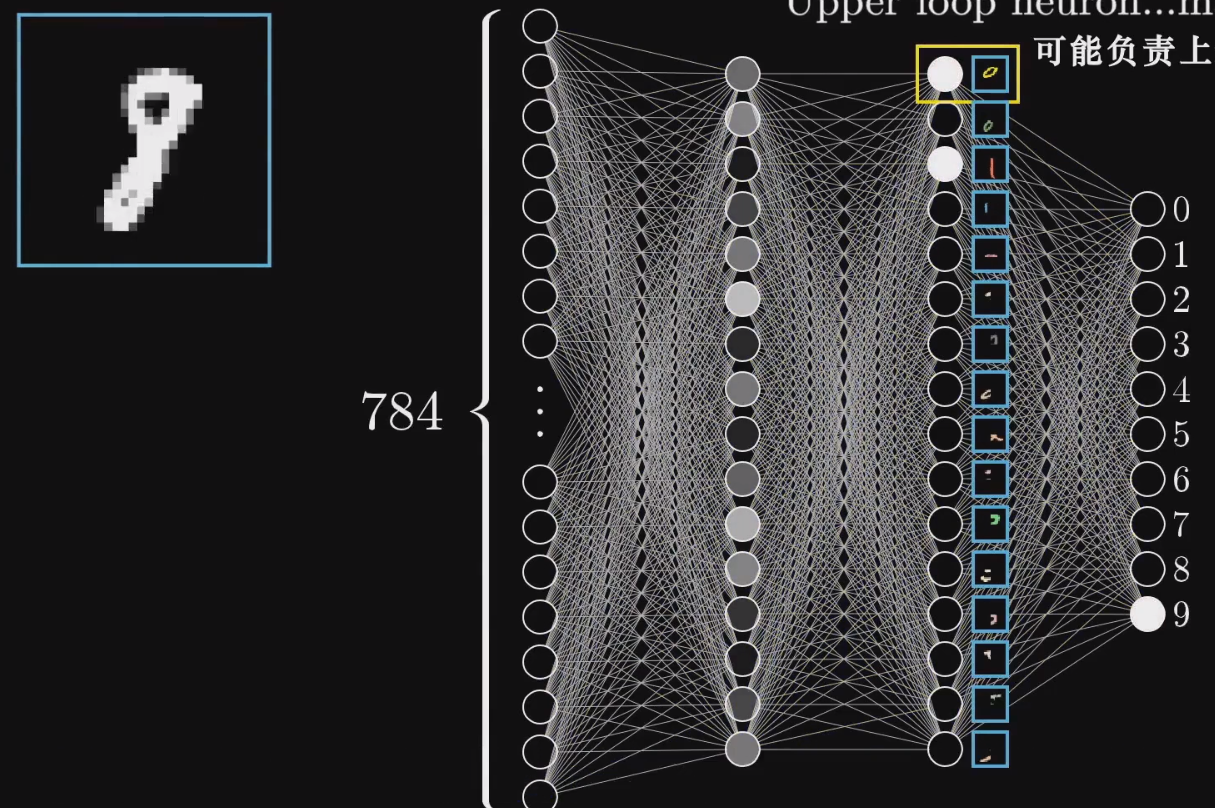
那么我们如何要识别这些部件呢?识别部件的任务可以拆分成更加细微的问题,即识别部件中更小的边。

所以,隐藏层的第一层就是识别更加细微的短边,然后将激活的短边组合成下一层的部件。
但是,神经网络真的是这样工作的吗?虽然,这个逻辑也看似合理。
下面我们会讲解这个猜测到底对不对。
权重和偏置
上面我们说了,一层的激活值影响下一层的激活值,但是究竟是怎么影响的?
即最开始的神经网络连接图中,每一个神经元连接的线究竟是什么?
让我们关注的更加细微一些,我们选取第二层的一个神经元来进行讲解。

我们的目的是这个神经元是不是就是对应一个短边。每一条连接神经元的线都是一个权重。

权重对应的只不过是数字而已,我们拿起第一层所有的激活值和他们对应的权重值,算出他们的加权和。
这里我们要注意的是,算出来的加权和对应任何一个实数,但是,我们想叫这个数,在网络中,只处于 0 - 1 之间。所以,我们需要一个激活函数将上面的实数进行压缩。
关于激活函数,你可以看我的另一篇 blog 。
我们再次解释一下这个激活函数的用途。
就拿 sigmoid 函数为例。
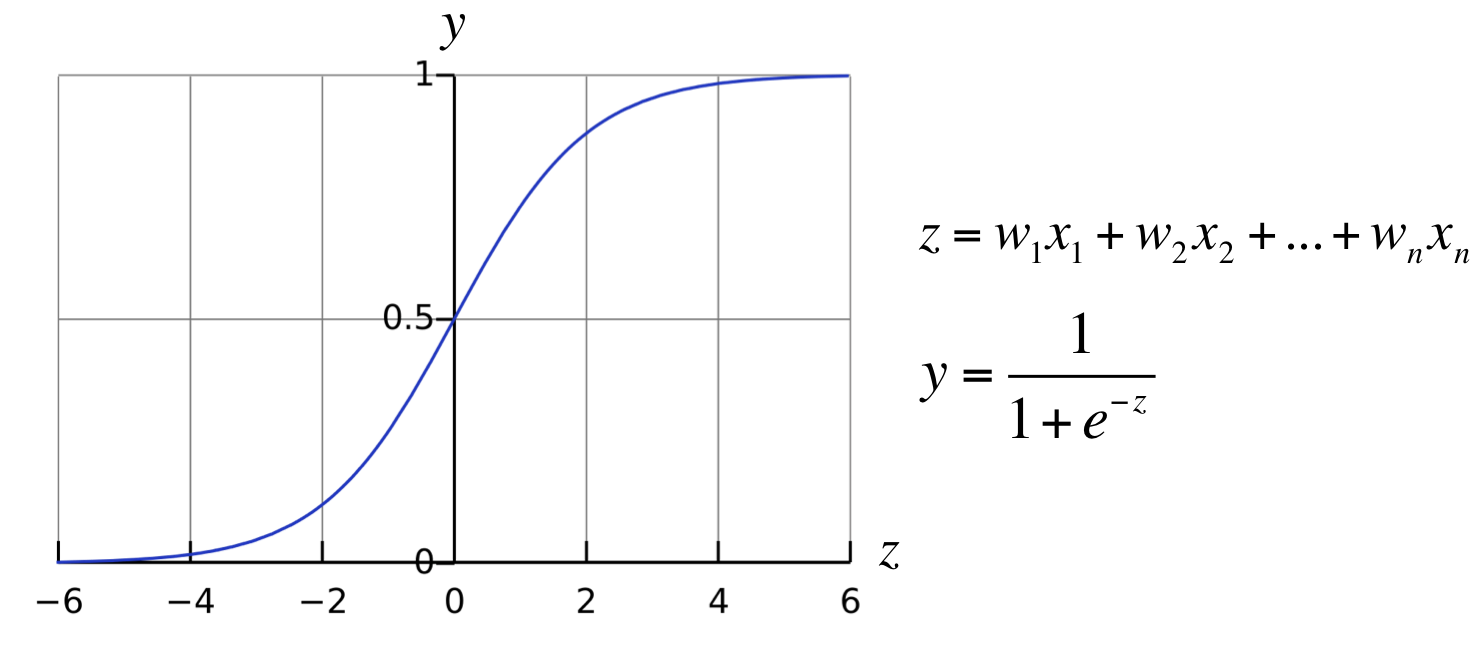
当数值很小的时候,我们的 sigmoid 会让他接近于 0 ,当数值很大的时候我们会让他接近于 1 ,中间那段是一段平滑的曲线。
所以,激活函数就是对一个加权和到底有多正打分,如果一个值很大,那么激活函数就会让这个值更加接近于 1 ,这个激活值,在下一层的神经网络中占据的加权和的比重也就越大。所以,这个神经元在某种意义上就是被激活。
但是,有时候,即便是加权和大于 0 的时候,我们也不想将这个神经元点亮,但是,当这个加权和大于 10 的时候,我们才希望它会点亮,所以我们在这里引入偏置。
我们只需要在加权和后面加上 -10 之类的数,就能够控制激活的程度。然后我们将其送到激活函数中进行激活。
σ(w1a1 + w2a2 + w3a3 + w4a4+ ... + wnan)
σ 是 sigmoid
加上偏置
σ(w1a1 + w2a2 + w3a3 + w4a4+ ... + wnan - 10)偏执告诉你,加权和得多大,才能让神经元得激发变得有意义。
我们解释完其中一个神经元,但是,第一层得 784 个神经元,都得和第二层的 16 个神经元相连接。每一个神经元连线都是一个权重,然后,每一个神经元都有一个偏置。
所以,对于第一层和第二层来说,我们一共有
784 * 16 个权重
16 个偏置第二层和第三层之间还有
16 * 16 个权重
16 个偏置还有第三层和第四层,总的来说,我们一共需要
784 * 16 + 16 * 16 + 16 * 10 个权重
16 + 16 + 10 个偏置
总共有 13002 个参数我们所谓的机器学习,就是电脑如何处理这 13002 个参数。
用矩阵表达的结果就是
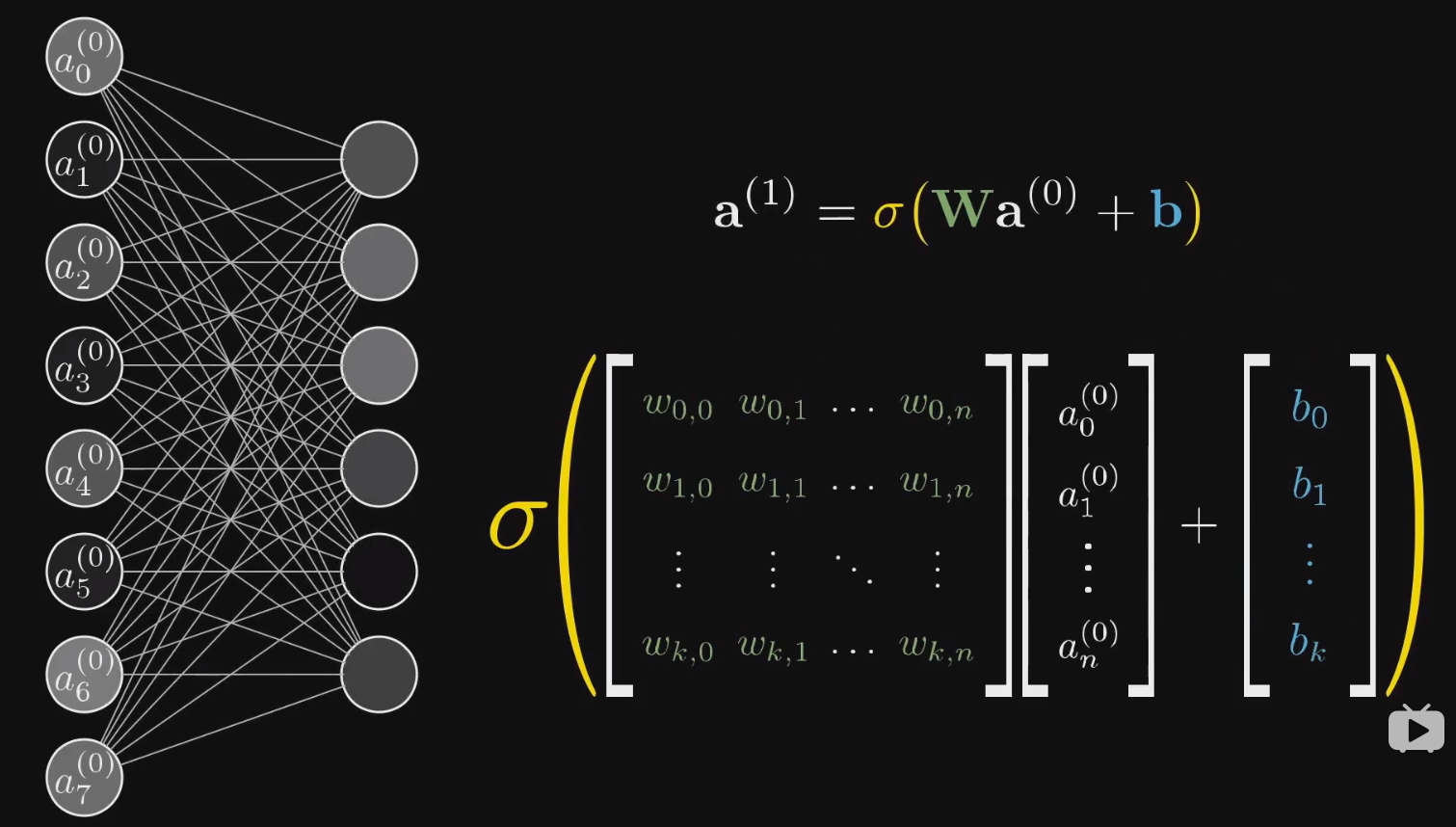
看到这里,我们可以说其实整个神经网络就是一个函数。一个输入为 784 个值,输出为 10 个值的函数。
前向传播
我们之前所展示的过程就是前向传播,第一层的激活值,决定第二层的激活值。每次这一层的激活值都会决定下一层的激活值。
梯度下降
调整 13002 个参数,总归是让人崩溃,所以,我们急需一个好的算法来有意识的调整这些参数。
我们认为每一个神经元都和上一层的所有神经元相连接,决定其激活值的加权和中的权重,有点像那些连接的强弱。而偏置值则表明神经元是否更容易被激活。
最开始,我们会随机初始化所有的权重和偏置值,毫无疑问,刚开始的模型是非常差的。
所以,我们要定义一个代价函数,告诉神经网络如何去改变。

我们只告诉训练模型有多糟糕是不行的,还得告知电脑如何去改变。
我们先以一元函数为例。
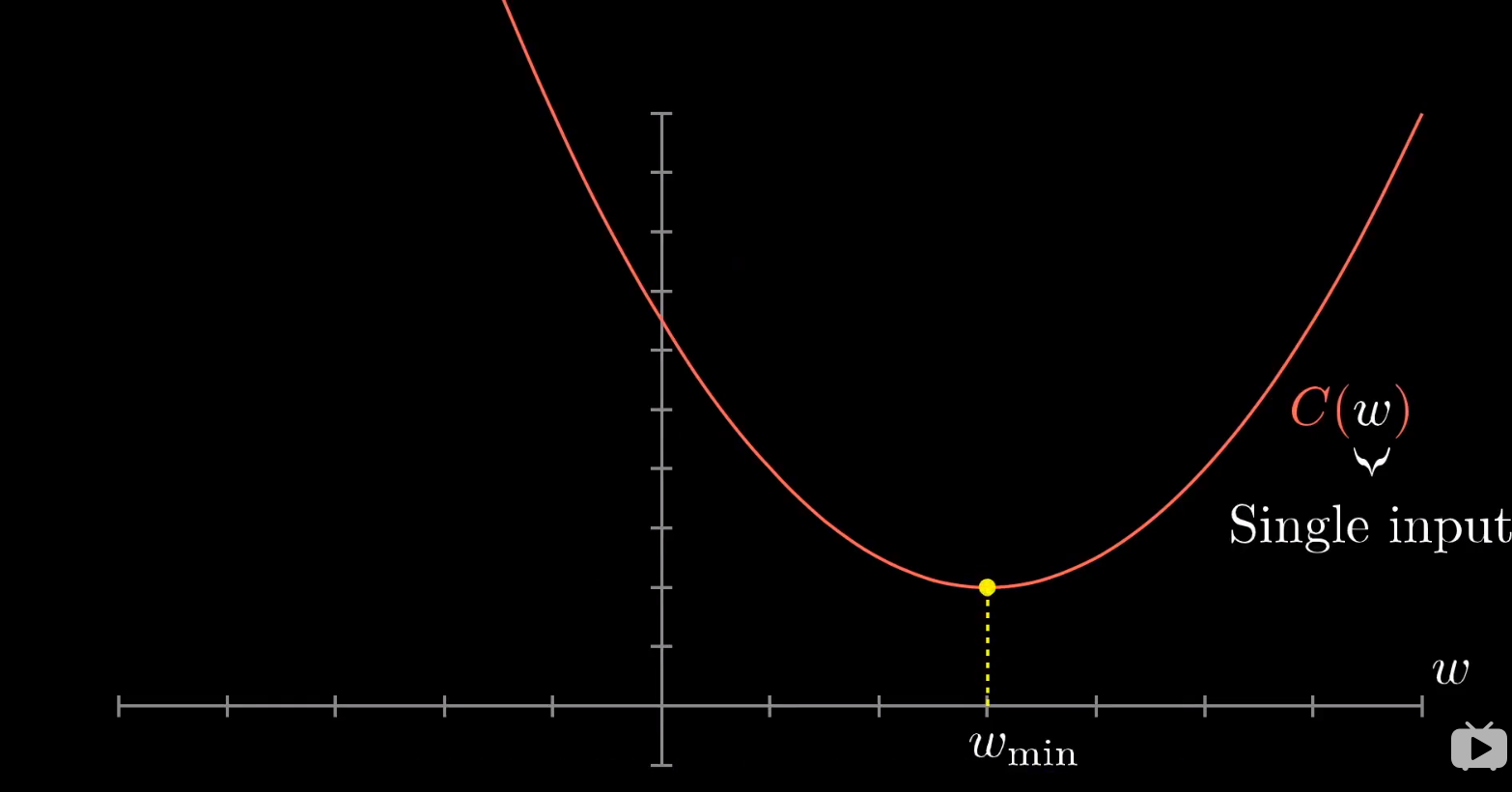
我们会如何找到一元函数的最小值?关于如何找到,我在其他 blog 中也有写,请移动到哪里观看。
我们因为是随机初始化一些参数,对于函数来说,我们就是随机将落点放在函数图像的任何一个部分。
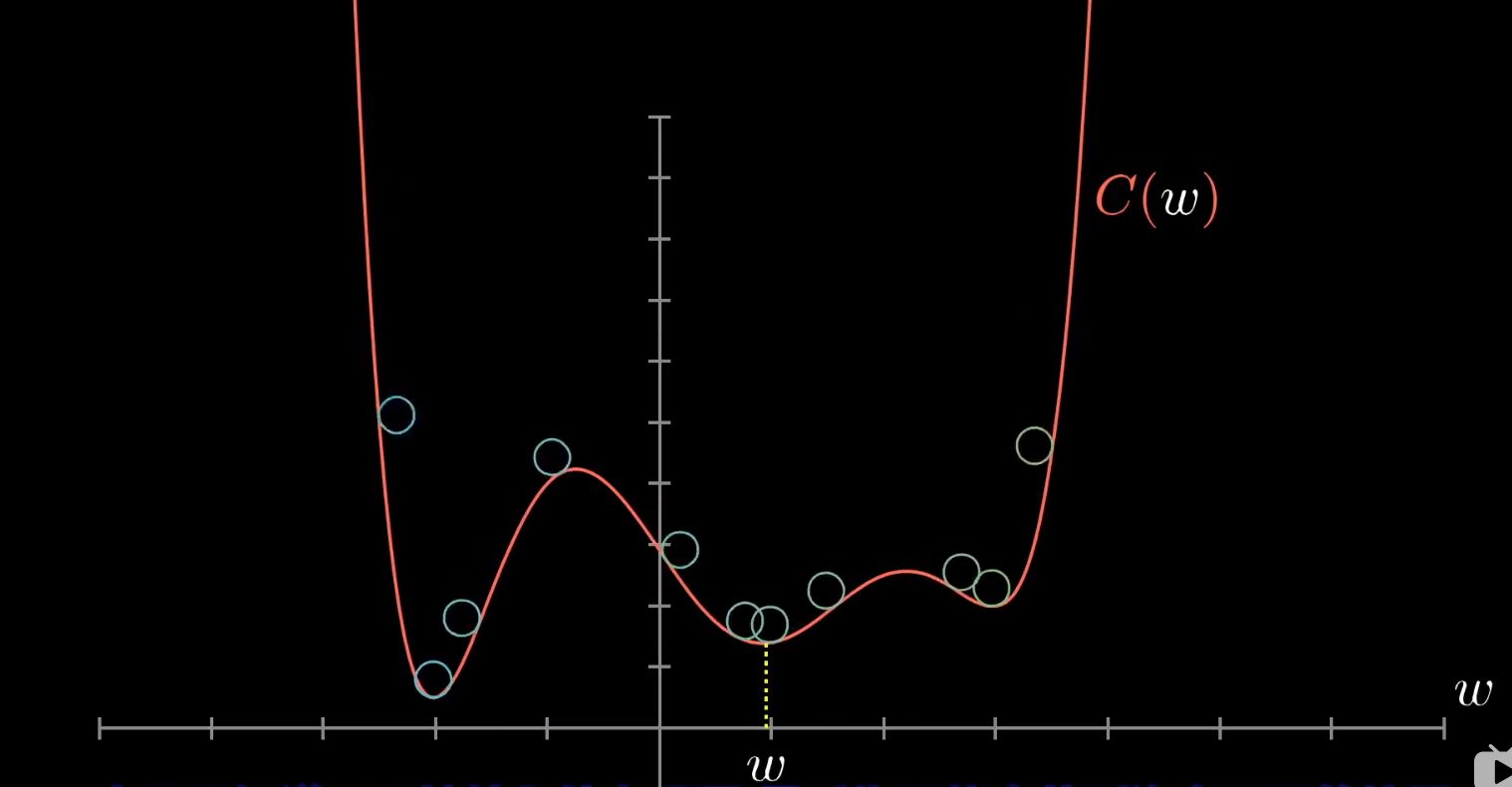
我们让小球进行滚动,但是,我们很容易陷入局部最小值。

关于什么是梯度,以及和导数之间的关系,请参考下面的 blog
我们的梯度沿着方向导数下降,只要方法得当就会到达最低点。
先计算梯度,再按梯度反方向走一下步下山,然后循环

对于处理 13002 个参数的函数,我们也是这个思路。
假设,将这 13002 个参数放在一个向量中,代价函数的负梯度不过也是一个向量而已。
将它们相加,就会得到更新后的参数。

在这里要注意的是,代价函数取了整个训练集的平均值,所以,代价函数最小化的意思是,对所有的样本得到的总体结果会好一点。
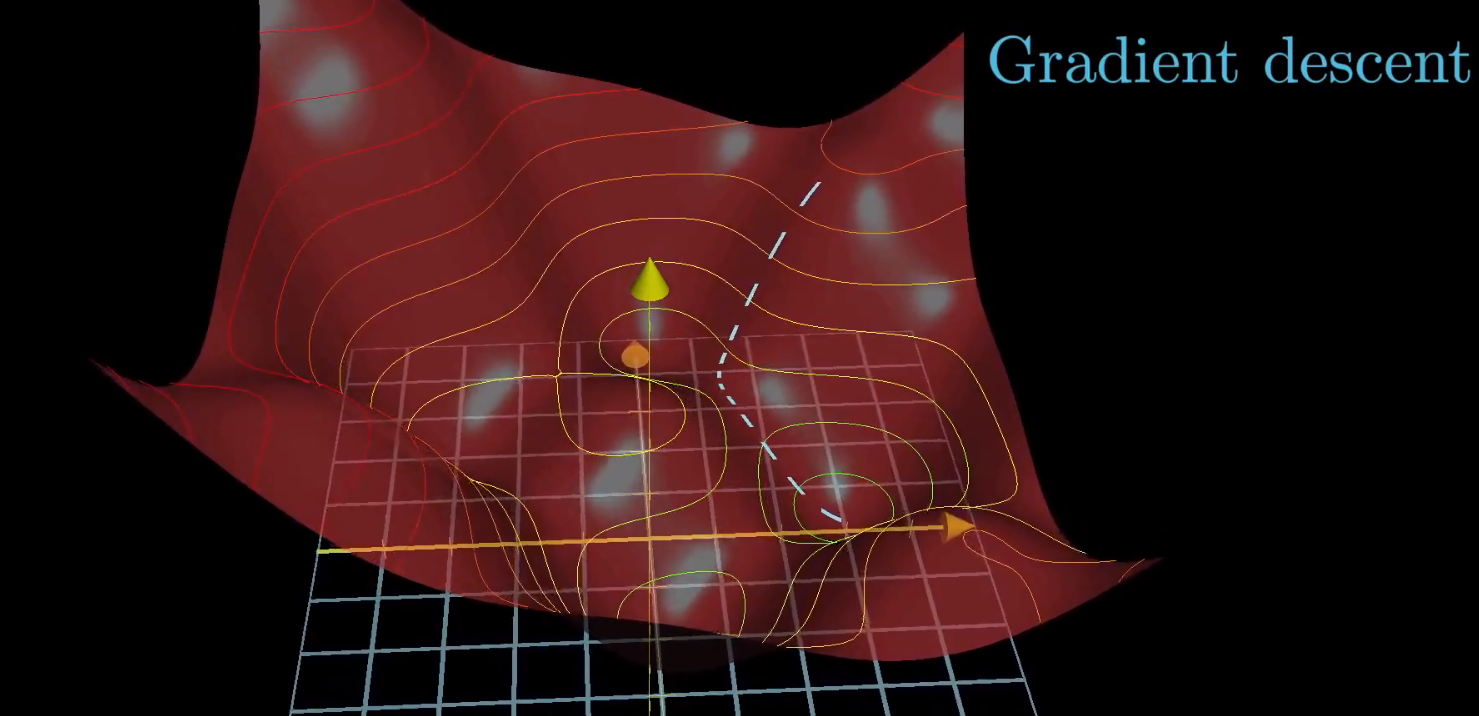
我们最终收敛到某一个坑中,这个坑其实就是代价函数制造的坑。
梯度的细节展现
我们的代价函数经过梯度转化后,有的数值变化大,有的数值变化小。

梯度的正负号告诉我们输入向量是该调大还是调小 ,但更重要的是,每一项的相对大小更告诉我们改变哪个值影响更大。
所以,在神经网络中我们调整一个权重就会比调整其他的影响更大。
所以,每一个梯度向量的大小可以理解为每个权重偏置的相对重要度,标记出那个参数的性价比更高。
向量越大,影响度越高。
比如,我们以一个二元方程为例。
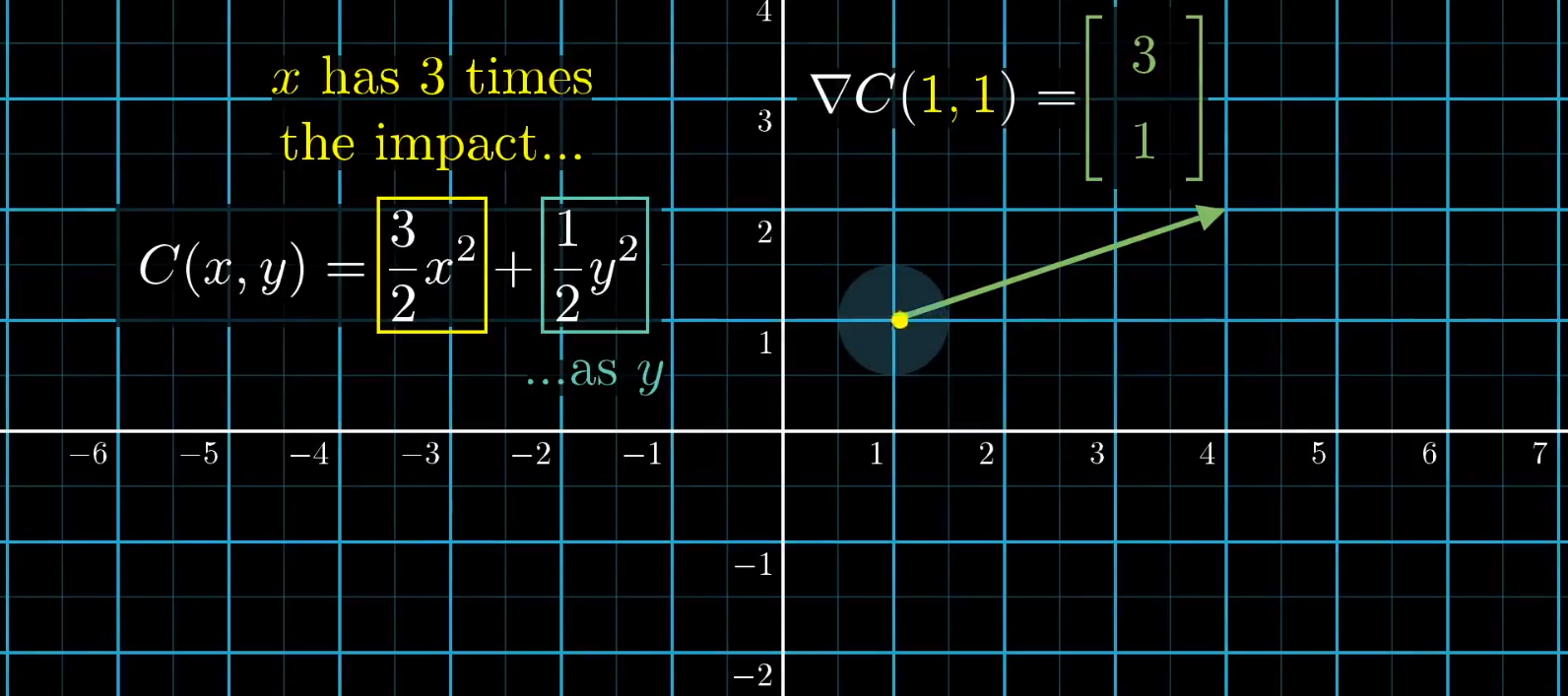
对于 (1,1) 点的梯度为 (3,1)
一种解读就是,你站在这个点上,顺着这个梯度的方向移动,函数值增加的最快。
另一种解读就是,第一变量的重要性是第二变量的 3 倍。也就是说,在这一块取值区域内,改变 x 的值会造成更大的影响。
我们的神经网络是将 784 个输入转化为 10 个输出,而我们的代价函数,是将 13002 个权重偏执作为输入,得到一个评分。
而代价函数的梯度则比代价函数还要复杂一层,其告诉我们该如何微调权重偏置的值,才能让代价函数变化得更快。
隐藏层究竟处理了什么
我在上面的曾经说过,隐藏层的第一层是识别短边,第二层是识别部件。
其实,完全不是,并且我们很难知道他们是怎么处理的。
一个很明显的例子就是,我们随机放一个噪声图像进去,神经网络图依然会很明确的给我们一个答案。
也就是说,虽然神经网络能很好地识别数字,但是他们并不会写数字。
反向传播
其实上面的梯度下降就是反向传播,通过降低代价函数,我们来调整权重和偏置。
学习就是找到特定的权重偏置,从而让一个代价函数最小化。
前向传播让激活值一层层的传递,而反向传播,让代价函数一点点的改变权重和偏置。
因为代价函数对成千上万个训练样本的代价取平均值,所以我们每一步基于梯度下降的权重调整也是基于所有的训练样本。
但是,这个计算量会特别特别大,所以,我们会从训练集中选取小部分进行训练。
我们会随机打乱训练数据,然后再每次取一小部分数据进行训练,这个方法又叫随机梯度下降。

当然,我们用小样本计算的梯度并不是真正的梯度,毕竟,真正的梯度是全部样本的集合。
但是,如果每次都获得真正的梯度,那么计算量实在是太大了。但是,用小样本计算也会得到一个不错的近似。

假设,我们用三维空间来表示小训练集的梯度下降的话,他的走路形态有点像醉汉的轨迹,虽然每一步不是最优,但是下降的速度很快。
如果,我们的训练集是是全部的话,我们虽然每一步都会按照最优路径下降,但是下降的速度会非常慢。
我们以一个训练数据为例。
以训练单个样本 2 为例。
假设,训练样本还没有训练好,那么输出层的激活值看起来就很随机。

我们不能改变激活值,但是能改变权重和偏置值。
我们希望输出为 2 ,那么我们希望第三个输出值变大,其他的数值变小。
而且,对于 2 来说,增加数字 2 神经元的激活值,应该比减少数字 8 的神经元的激活值来的更加重要。
如果我们要增加 2 的激活值,我们有三条路可以走
增加偏置 b
增加权重 w
为什么前两个都是增加,而不是改变,因为我们的目的是让目标的激活值更大
改变激活值 a
这个是改变的原因是激活值的增大变小都有可能会增加激活值,毕竟,激活值也有正负的
改变权重
每个权重的影响力是不同的。
连接前一层最亮的(也就是激活值最大的)神经元的权重,影响最大。因为这些权重会与大的激活值相乘。
所以,对于 2 这个训练样本来说,增加这几个权重,最终会对代价函数造成影响,比增加暗淡的神经元的值效果大上好几倍。
当我们说梯度下降的时候,并不关心那个系数增加还是减小,而是看那个参数的性价比更高。
第三个改变激活值,就是改变前一层的激活值。
如果所有正权重连接的神经元更亮,所有负连接的神经元更暗的话,那么数字 2 的神经元就会更强烈的激发。
当然,我们不能直接改变激活值,我们只能控制权重和偏置。
但是,从全局来看,这只不过是数字 2 的神经元所期待的变化。每一个训练样本,都有各自想要激活的想法。
所以,我们会将所有的样本进行整合,将所有的期待的改变加起来,就得到了一串对倒数第二层改动的变化量。
我们改变倒数第二层的变化量之后,就可以继续改变倒数第三层。这样层层向后传递,就是我们所有的反向传播。
在这里我们需要注意的是:
我们将所有的训练样本一起整合,然后再用这些整合的数据改变倒数第二层和倒数第一层的权重和偏置。
再用改变了的激活值去影响上一层的权重和偏置。(这句话可能有点问题,因为我们是得不到改变的激活值的,但是,在下面的数学推导公式中,我们会详细的讲解如何进行反向传播)
而不是,一个数据一个数据的进行改变传播。数学推导
详情见我的另一篇 blog 。