姑苏城外一茅屋，万树梅花月满天

0%

signal | 时频图的绘画

发表于 更新于 分类于 ， Valine：

时频图看起来挺高大上的。。。


参考资料



看前阅读



pywt


pywt库的全称是PyWavelets，安装方式自己搜索。

根据

得知，我们选择

  • 连续小波变换（Continuous Wavelet Transform (Scalogram)）

方法说明

  • 小波变换是一种线性时频表示，它保留了时间偏移和时间尺度。
  • 连续小波变换能很好地检测非平稳信号中的瞬态信号，对瞬时频率增长较快的信号也有很好的检测效果。
  • CWT是可逆的。
  • CWT使用可变大小的窗口平铺时间-频率平面。窗口会在时间上自动加宽，使其适合低频现象，而对于高频现象则会变窄。

适用场合

  • 心电图（ECG）：ECG信号最有用的临床信息是在其连续波和由其特征定义的振幅之间的时间间隔中发现的。小波变换将心电信号分解成不同的尺度，使得分析不同频率范围的心电信号更容易。
  • 脑电图（Electroencephalogram，EEG）：原始EEG信号存在空间分辨率低、信噪比低和伪影等问题。含噪信号的连续小波分解在不改变噪声随机分布的情况下，将信号的内在信息集中在几个具有较大绝对值的小波系数中。因此，可以通过对小波系数进行阈值化来实现去噪。
  • 信号解调：使用自适应小波构造方法解调扩展二进制相移键控（EBPSK）。
  • 深度学习：CWT可以用来创建时频表示，可以用来训练卷积神经网络。利用小波分析和深度学习对时间序列进行分类展示了如何利用尺度图和转移学习对心电信号进行分类。

我们选择 cwt。

官方的文档

说句实话，这个函数，我还没见到国内有人详细解读，我在这里也只是，浅尝辄止，可能不是很准确。


pywt.cwt(data, scales, wavelet)

Parameters:

  • data : array_like
    • 信号本身
  • scales : array_like
    • 范围？具体还是从例子中得到吧
  • wavelet : Wavelet object or name
    • 选择的小波名字
  • sampling_period : float
    • 1 / 频率 「具体看下面的例子」

例子


1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    x = np.linspace(0, 1, 1400)
    y = 7 * np.sin(2 * np.pi * 200 * x) + 5 * np.sin(2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x)
    wavename = 'cgau8'
    totalscal = 256
    # 中心频率
    fc = pywt.central_frequency(wavename)
    cparam = 2 * fc * totalscal
    scales = cparam / np.arange(totalscal, 1, -1)
    [cwtmatr, frequencies] = pywt.cwt(y, scales, wavename, 1.0 / 1400)
    plt.figure(figsize=(8, 4))
    plt.contourf(x, frequencies, abs(cwtmatr))
    plt.show()


if __name__ == '__main__':
    test()

可以看出，这是由 200HZ、400HZ 和 600HZ 组成。

下面依次解释上面的取值，建议你先看一下

首先最大频率是 600 ，所以，为了能还原模拟信号，我们选择取样率为 1400/s 也就是赫兹是 1400 的。这也就是

x = np.linspace(0, 1, 1400)

模拟，1 秒内 1400 的取样点。

接着就是

fc = pywt.central_frequency(wavename)
cparam = 2 * fc * totalscal
scales = cparam / np.arange(totalscal, 1, -1)

这个还没理解，但是，后面会做例子来解释。

[cwtmatr, frequencies] = pywt.cwt(y, scales, wavename, 1.0 / 1400)

这个就是进行 cwt 分解。

图为

改变频率组合

只保留 600 的频率。

1
2
3
4
5
6
7
8
9
10
11
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    y = 3 * np.sin(2 * np.pi * 600 * x)
    ...

if __name__ == '__main__':
    test()

保留 400 和 600 的频率

1
2
3
4
5
6
7
8
9
10
11
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    y = 5 * np.sin(2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x)
    ...

if __name__ == '__main__':
    test()

保留 200 和 400 的频率

1
2
3
4
5
6
7
8
9
10
11
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    y = 5 * np.sin(2 * np.pi * 200 * x) + 3 * np.sin(2 * np.pi * 400 * x)
    ...

if __name__ == '__main__':
    test()

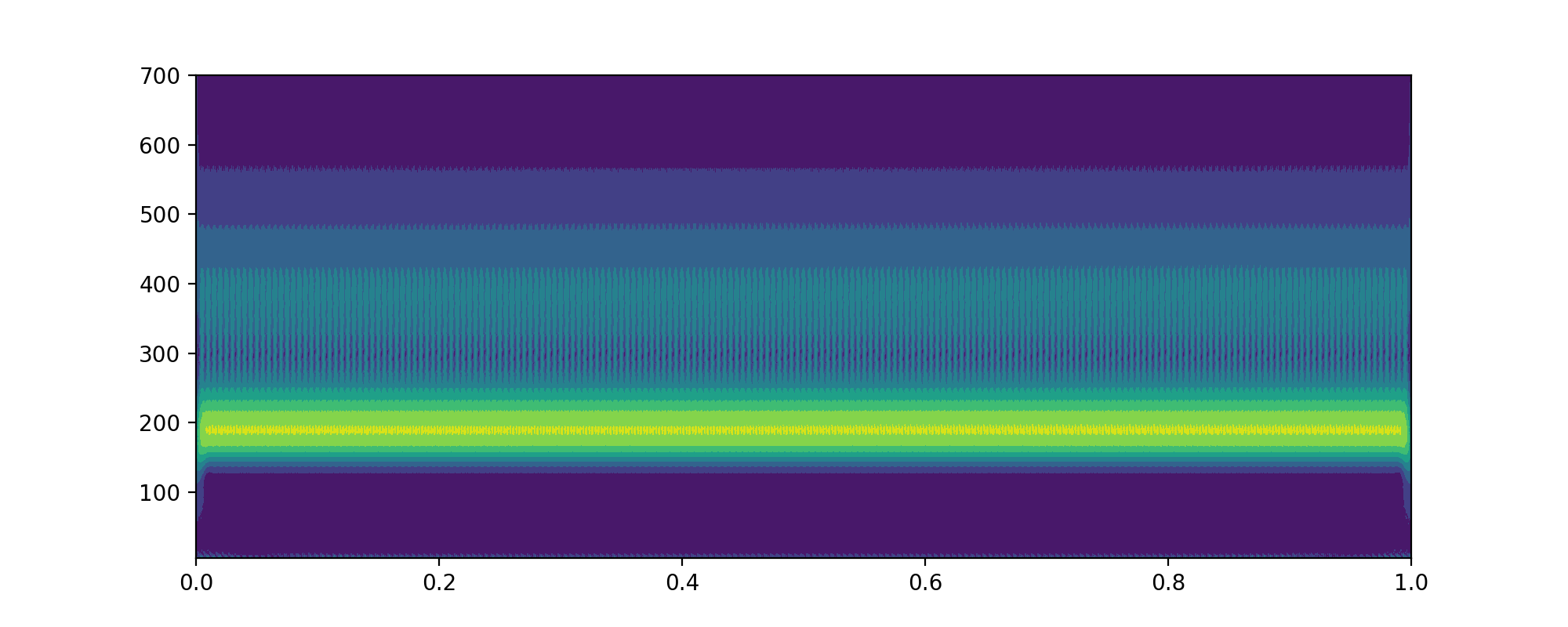
这里可以看出，图中亮的部分是频率的具象表现。

改变采样频率

最开始的时候，我们用的是 1400 的采样频率，图为

为 2000 的时候

1
2
3
4
5
6
7
8
9
10
11
12
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    x = np.linspace(0, 1, 2000)
    ...
    [cwtmatr, frequencies] = pywt.cwt(y, scales, wavename, 1.0 / 2000)

if __name__ == '__main__':
    test()

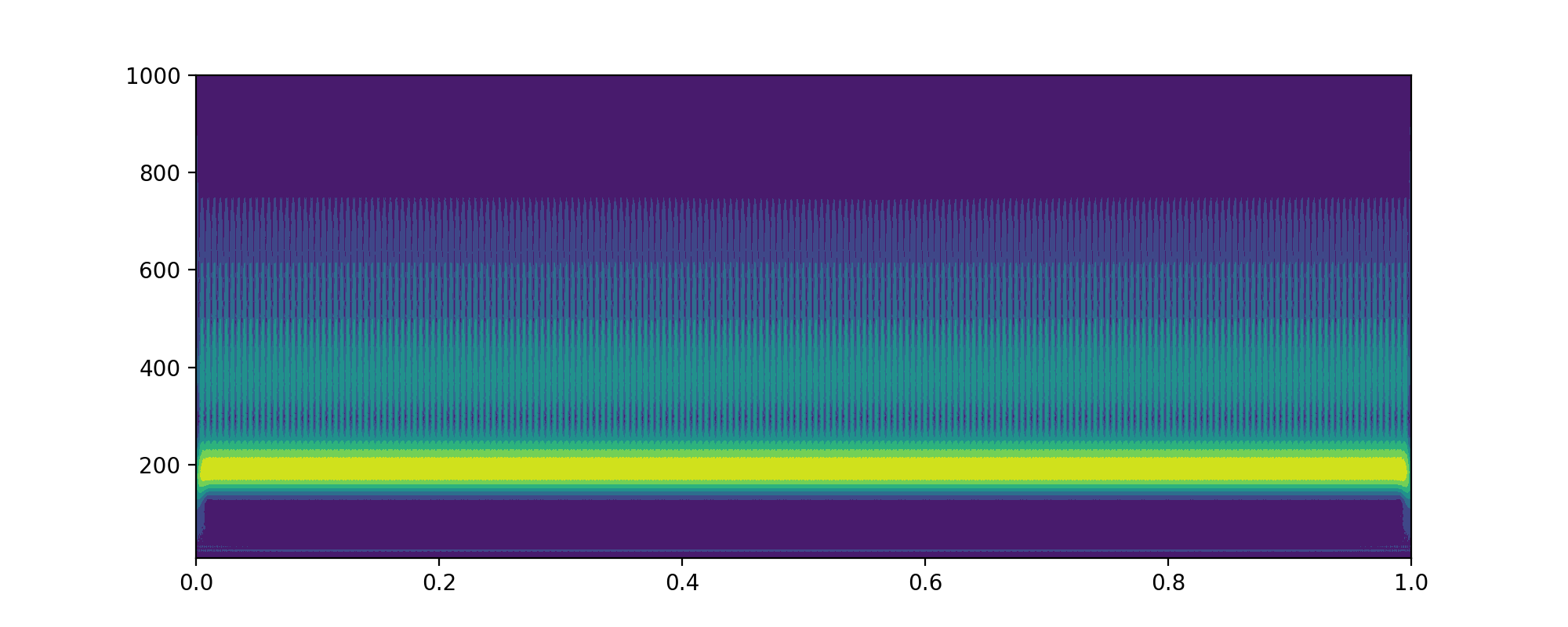
为 1000 的时候

1
2
3
4
5
6
7
8
9
10
11
12
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    x = np.linspace(0, 1, 1000)
    ...
    [cwtmatr, frequencies] = pywt.cwt(y, scales, wavename, 1.0 / 1000)

if __name__ == '__main__':
    test()

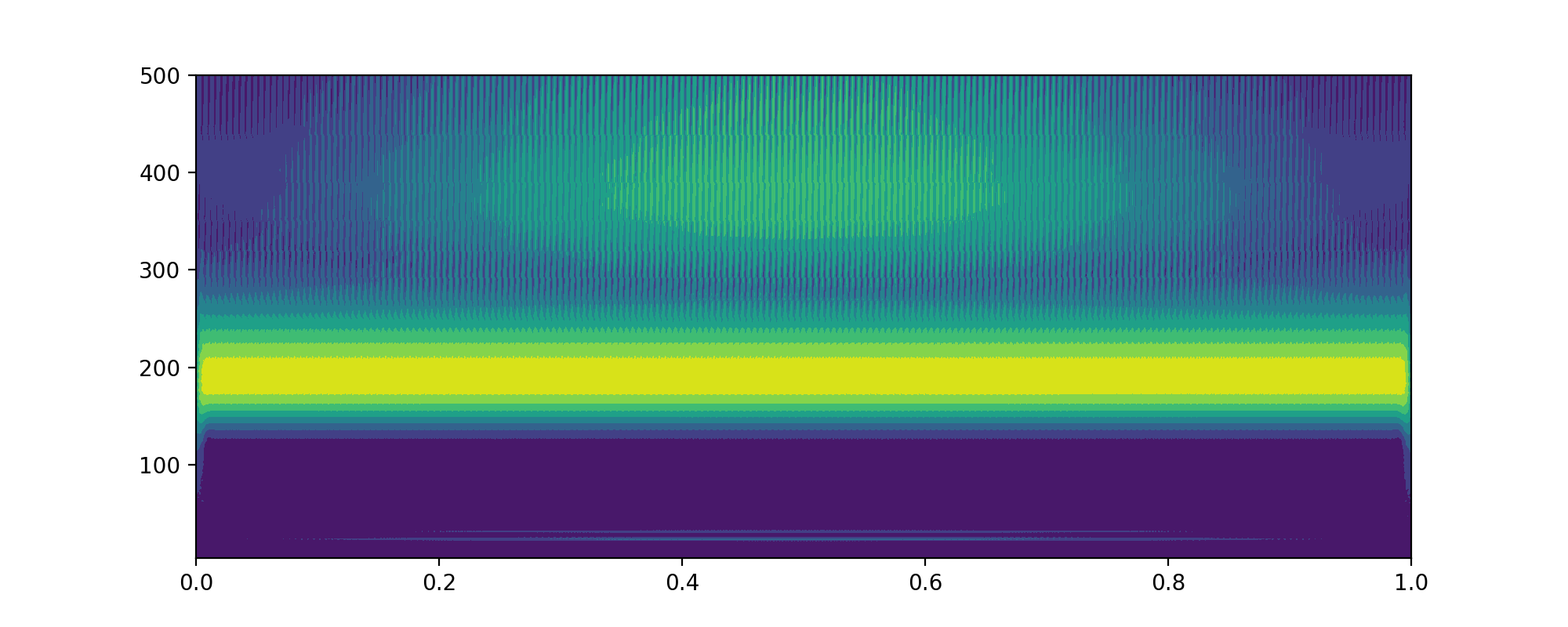
可以看出已经丢失了一部分信息。

在这里我们也看出来采样频率的重要性，一定要大于最高频率的两倍才行。

另外，我们可以看到纵轴是采样频率的一半。我猜测是取了一半，理论支撑来自于

小波类型

这个可以从

print(pywt.wavelist())

得到有多少 wavename 支持。

原来的为

wavename = 'cgau8'

换成

wavename = 'morl'

变成

有很多，但是，具体怎么区分，我也不知道。。。

ps: 并不是所有的 wavename 都能用，具体为什么，我不知道

scales 范围的变化

具体的代码在

totalscal = 256
# 中心频率
fc = pywt.central_frequency(wavename)
cparam = 2 * fc * totalscal
scales = cparam / np.arange(totalscal, 1, -1)
[cwtmatr, frequencies] = pywt.cwt(y, scales, wavename, 1.0 / 1400)
print(cwtmatr)

我理解，scales 是范围或者层次的意思。

首先，我得说，我不知道

fc = pywt.central_frequency(wavename)

这个所谓的中心频率是什么意思。。。

如果把上面代码的 scales 改成

scales = cparam / np.arange(1, totalscal, 1)

图像是

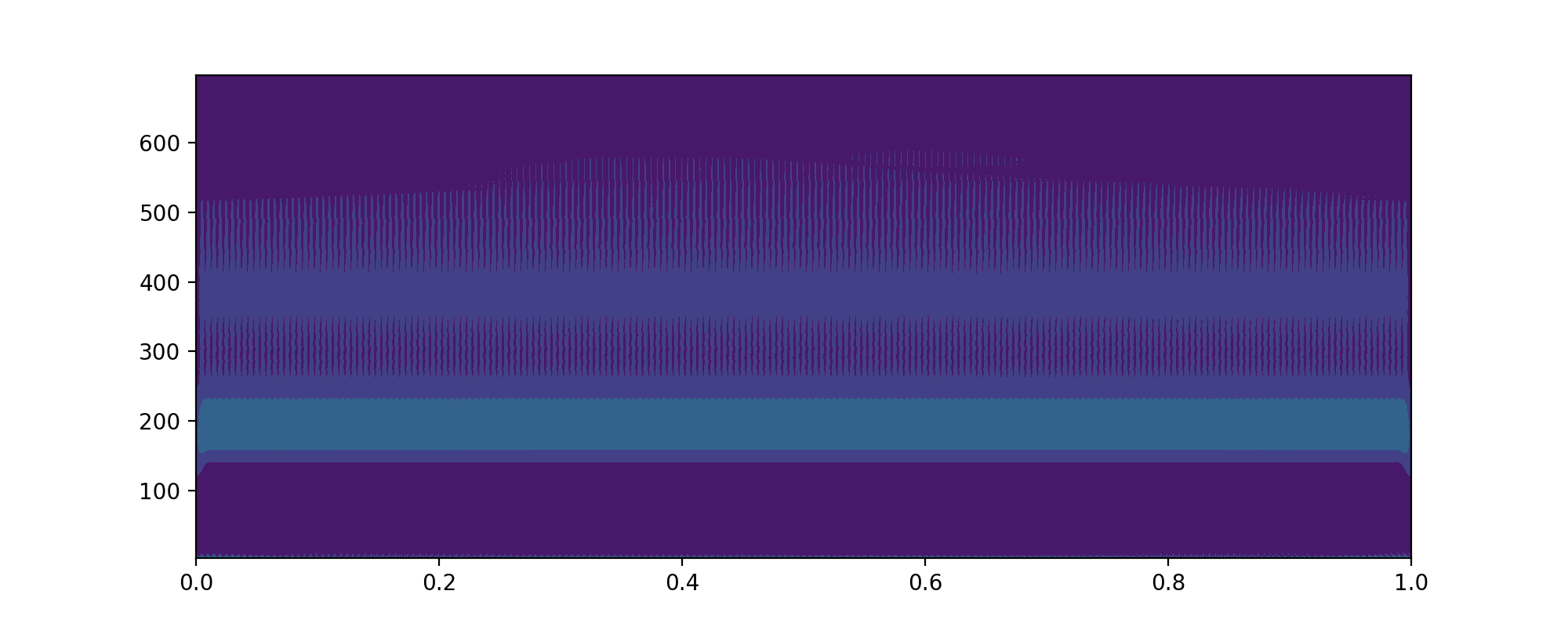
然后我们在 print 打上断点

  • 当 totalscal = 256 的时候
    • cwtmatr 的 shape 为 (255,1400)
    • frequencies 的 shape 为 (255,)

图像为

  • 当 totalscal = 100 的时候
    • cwtmatr 的 shape 为 (99,1400)
    • frequencies 的 shape 为 (99,)

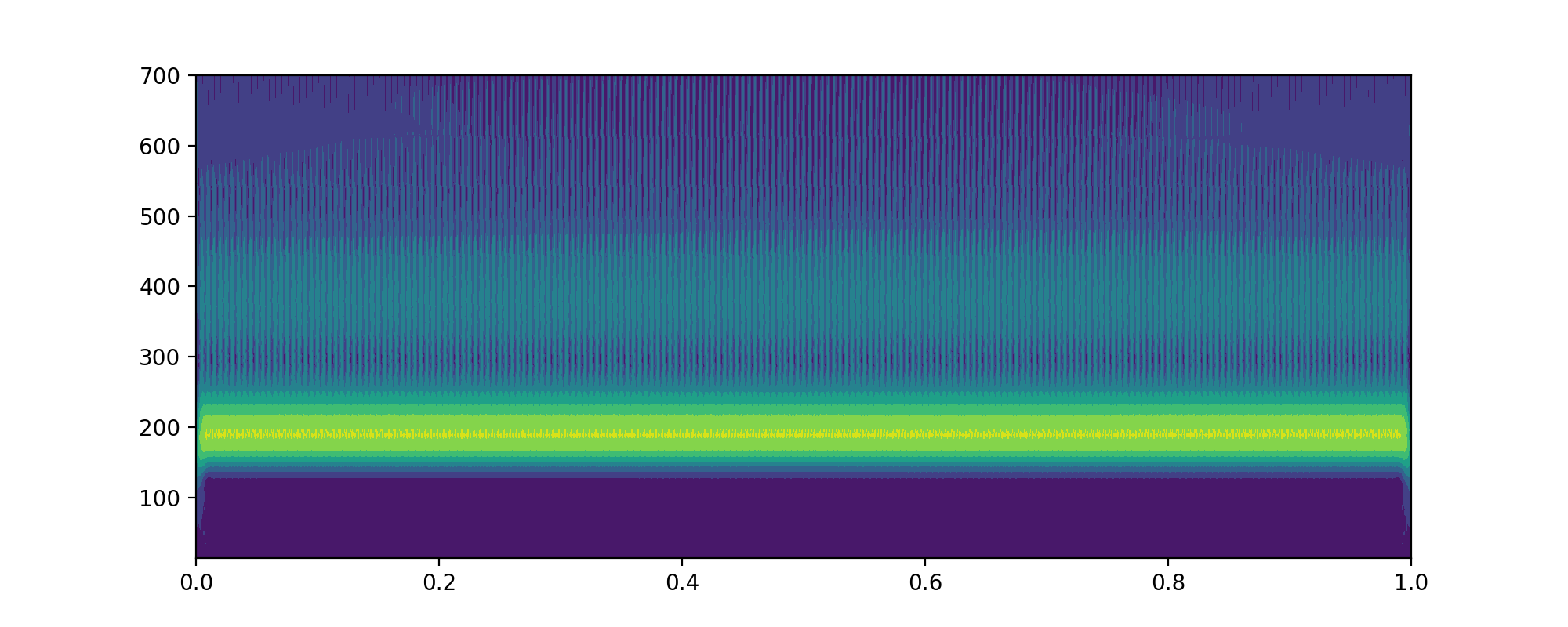
  • 当 totalscal = 50 的时候
    • cwtmatr 的 shape 为 (49,1400)
    • frequencies 的 shape 为 (49,)

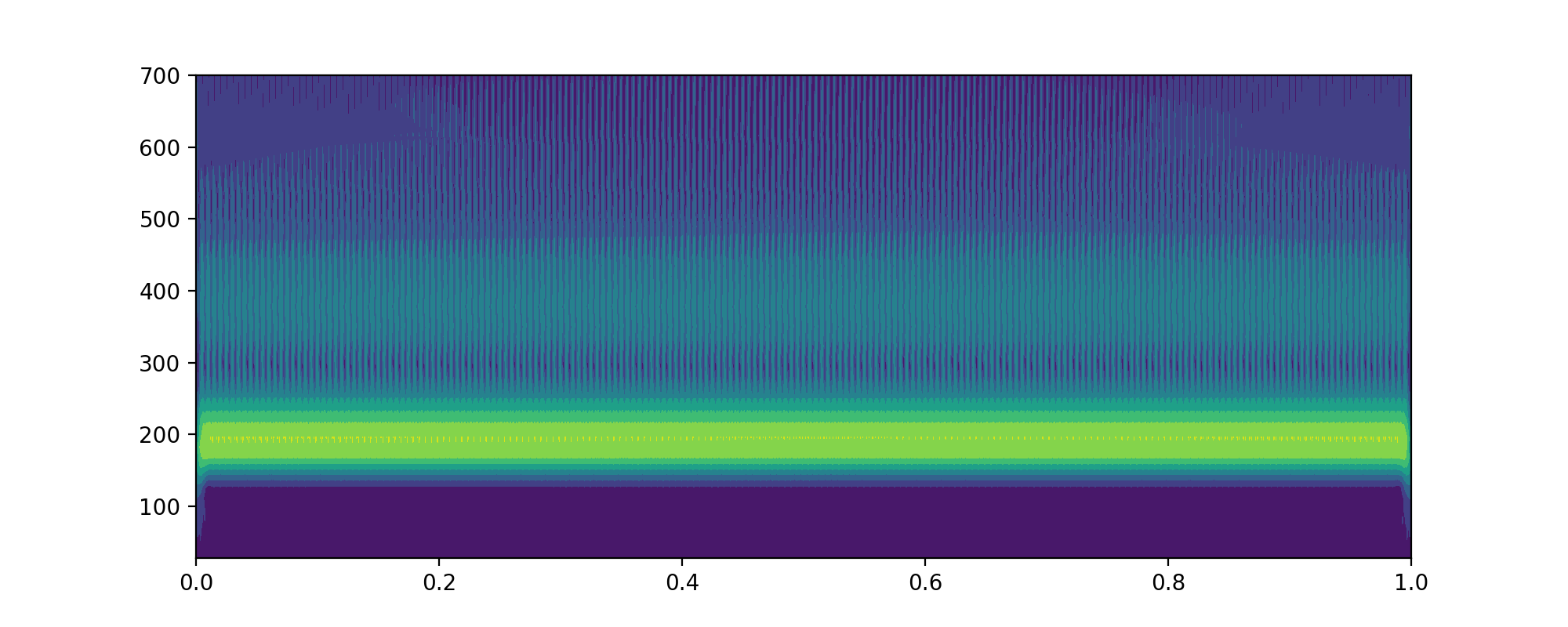
  • 当 totalscal = 10 的时候
    • cwtmatr 的 shape 为 (9,1400)
    • frequencies 的 shape 为 (9,)

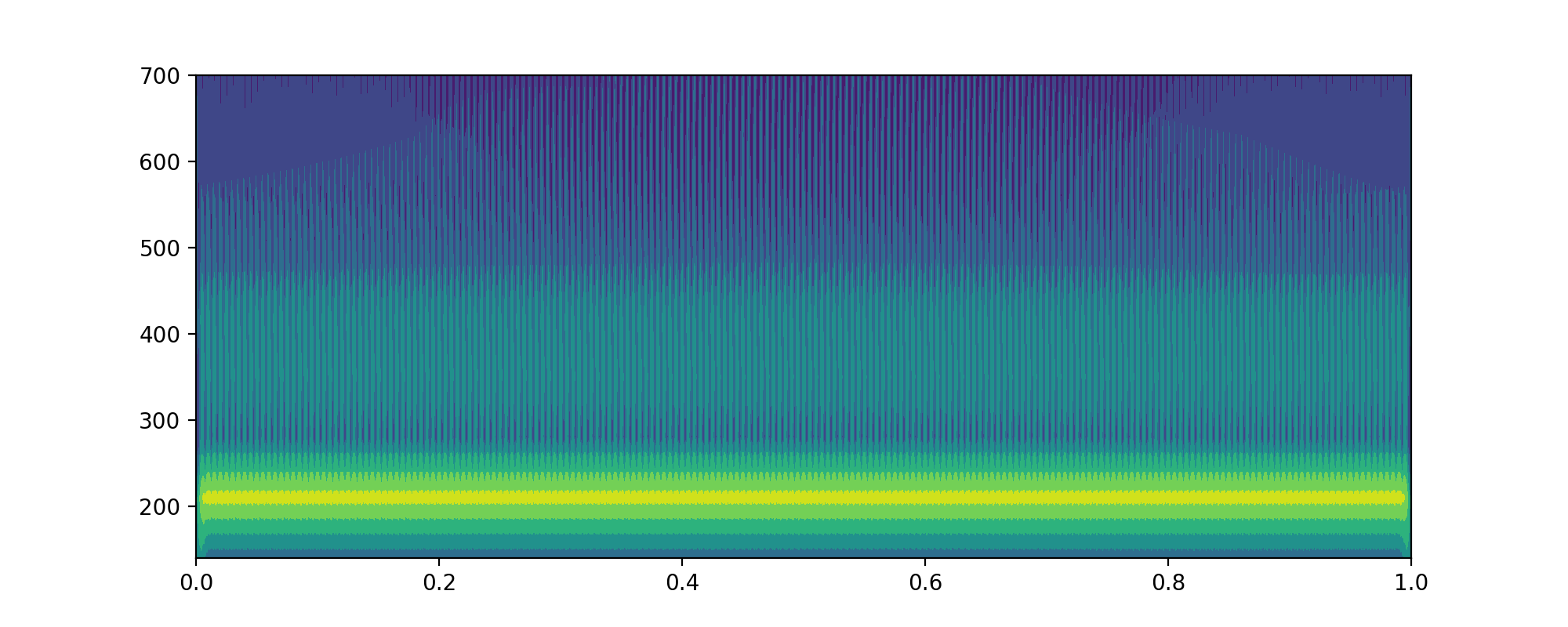
  • 当 totalscal = 500 的时候
    • cwtmatr 的 shape 为 (499,1400)
    • frequencies 的 shape 为 (499,)

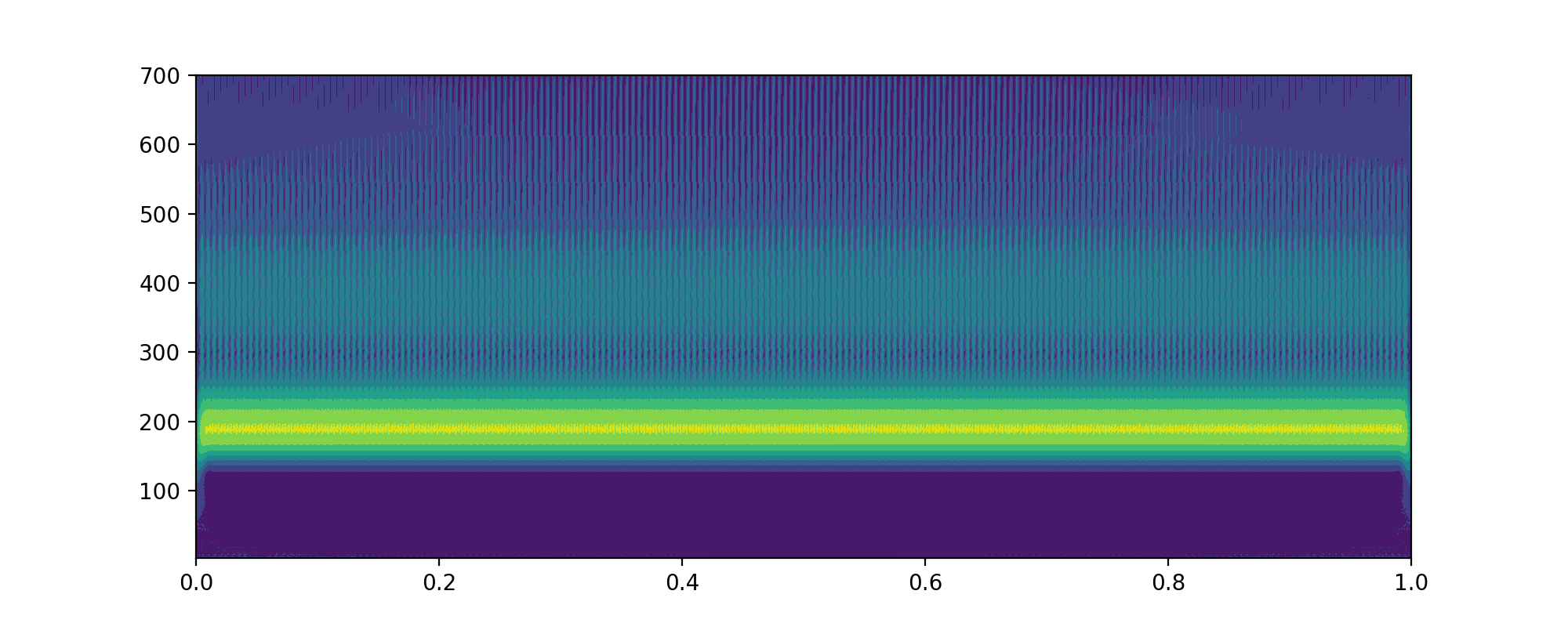
totalscal 不能为 1，2，具体我认为是这个代码的原因，根本原因，貌似需要后面处理大于 2 。

可以看出，这个值代表的是层次。

并且，并不是越大越好。

绘图函数

1
2
3
plt.figure(figsize=(10, 4))
plt.contourf(x, frequencies, abs(cwtmatr))
plt.show()

这个表现为

加入把 abs 去掉。

1
plt.contourf(x, frequencies, cwtmatr)

还有人将

plt.contourf 替换为 plt.pcolor

1
2
3
plt.figure(figsize=(10, 4))
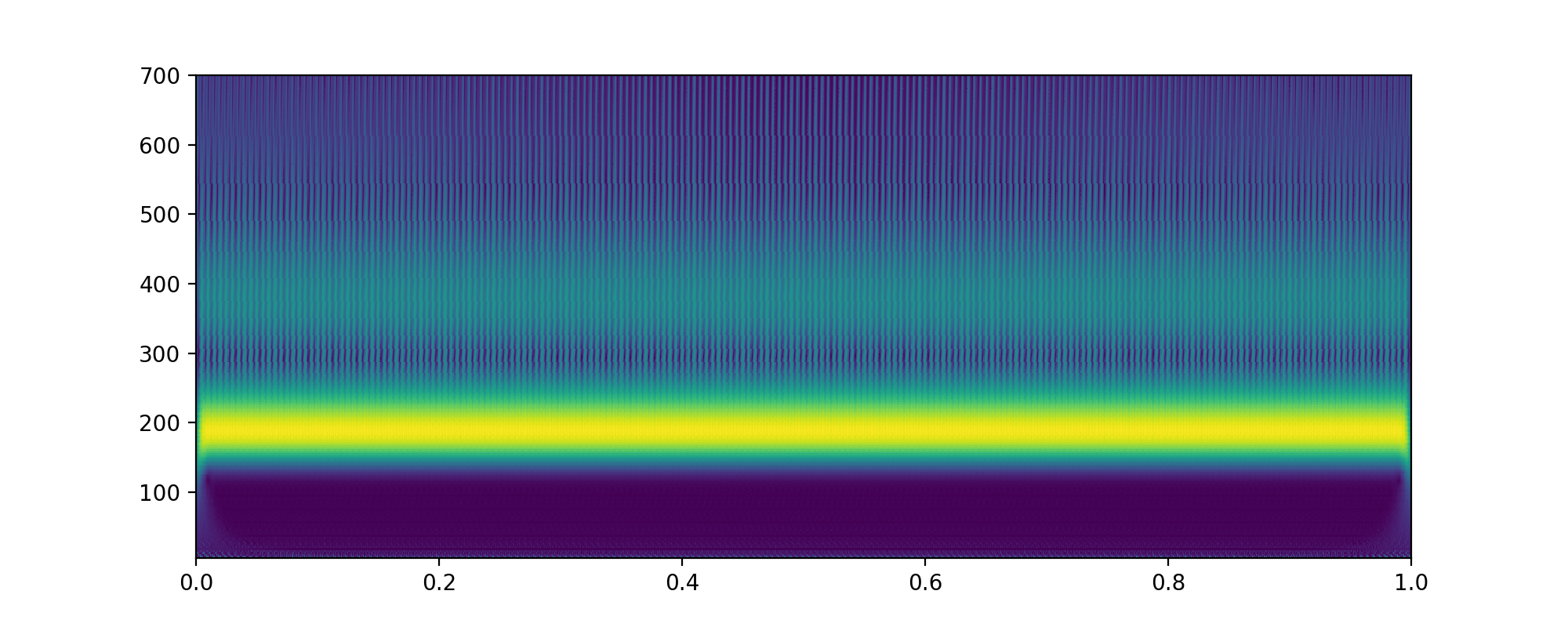
plt.pcolor(x, frequencies, abs(cwtmatr))
plt.show()

这样做有一个缺点就是运行速度非常慢。

所以，有人用

1
2
3
plt.figure(figsize=(10, 4))
plt.pcolormesh(x, frequencies, abs(cwtmatr))
plt.show()

进行替代，得到

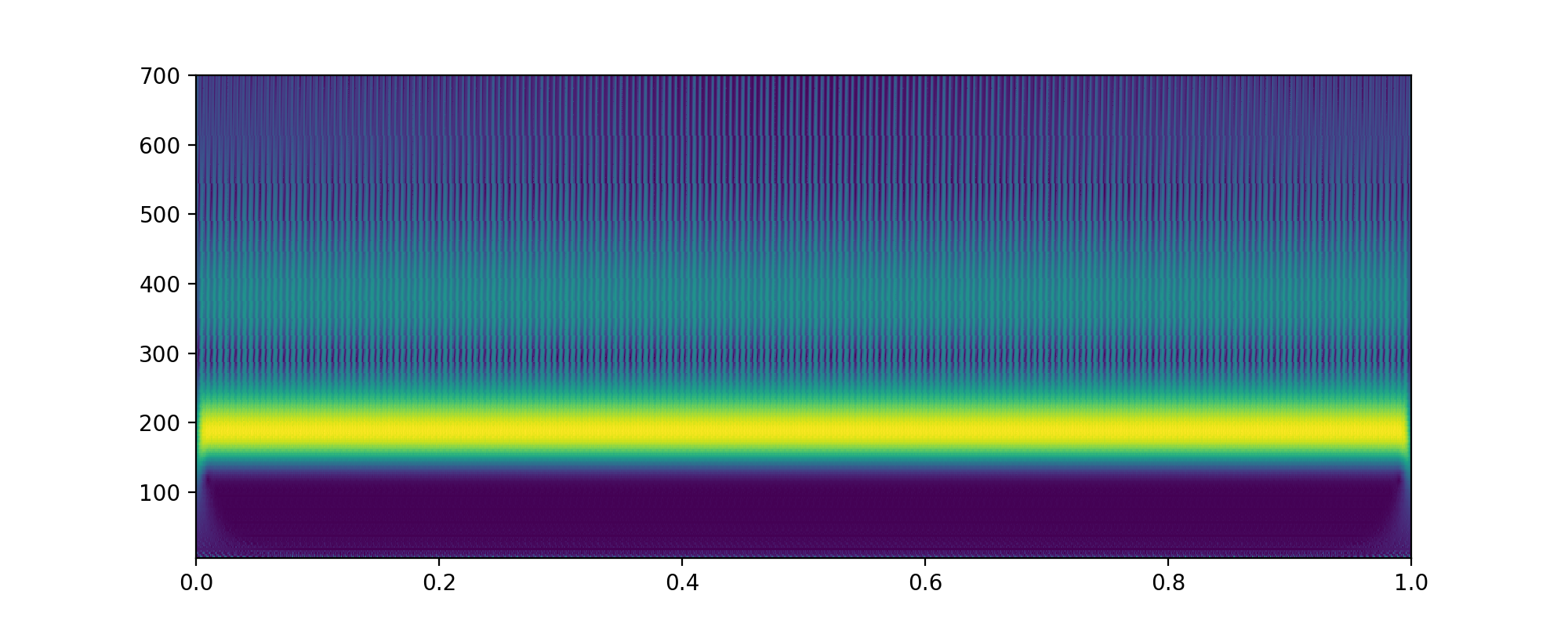
contourf 和 pcolor 的区别

  • contour
  • contourf

都是画三维等高线图的，不同点在于contour() 是绘制轮廓线，contourf()会填充轮廓。

不打算补充了，就这样吧。。。


多频率


假如我们把多个频率不叠加，而是放在不同的位置，比如:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    t = np.arange(0, 1.0, 1.0 / 500)
    a = 7 * np.sin(2 * np.pi * 200 * t)
    b = 5 * np.sin(2 * np.pi * 400 * t)
    c = 3 * np.sin(2 * np.pi * 600 * t)
    #
    d = np.concatenate((a, b, c), axis=0)
    t = np.arange(0, 1.0, 1.0 / 1500)
    wavename = 'cgau8'
    totalscal = 256
    fc = pywt.central_frequency(wavename)
    cparam = 2 * fc * totalscal
    scales = cparam / np.arange(totalscal, 1, -1)
    [cwtmatr, frequencies] = pywt.cwt(d, scales, wavename, 1.0 / 1500)
    plt.figure(figsize=(10, 4))
    plt.contourf(t, frequencies, abs(cwtmatr))
    plt.show()


if __name__ == '__main__':
    test()

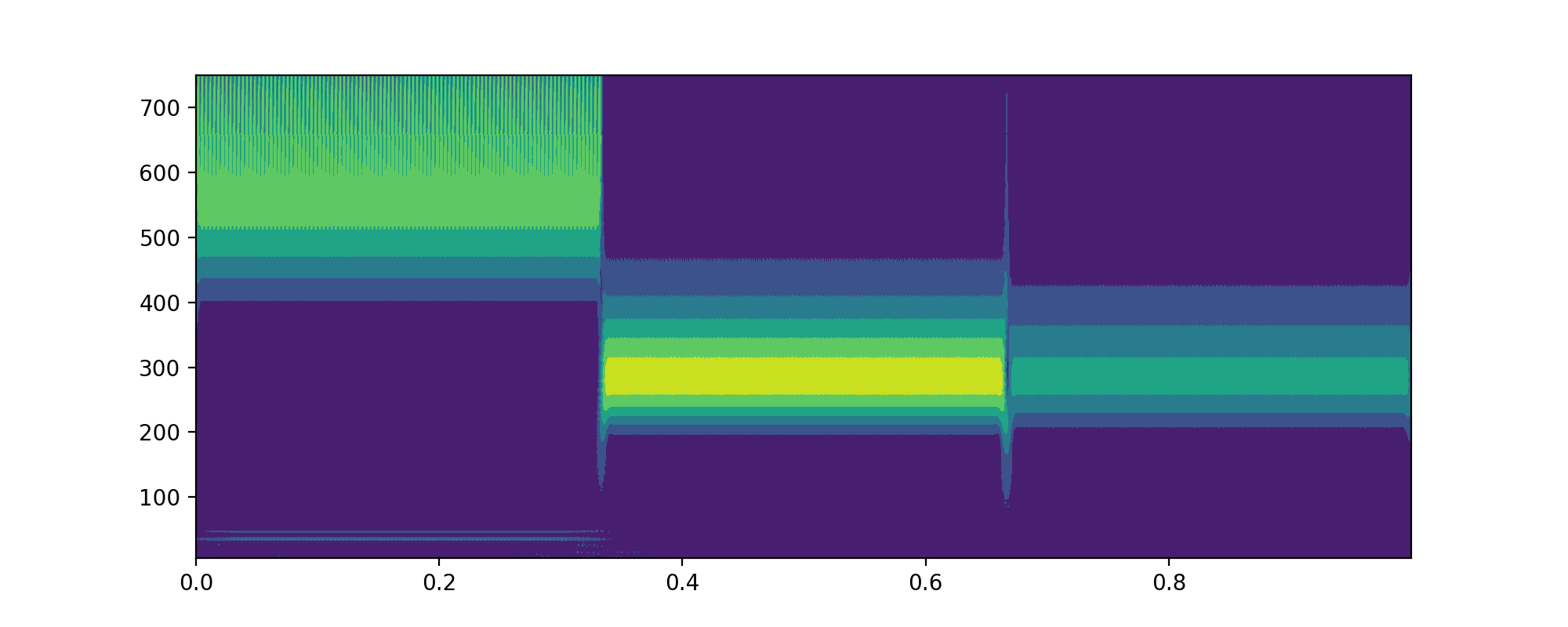
可以看到整个构造非常奇怪

  • 200HZ 的图像在 最上面，而其他 HZ 表现的也非常奇怪。

这个主要是程序写的不对。

我们虽然进行了 a,b,c 的拼接，但是，没有在 x 的顺序上拼接，而是，每次都在 np.arange(0, 1.0, 1.0 / 500) 上拼接。

正确的代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    t = np.arange(0, 1.0, 1.0 / 1400)
    a = 7 * np.sin(2 * np.pi * 200 * t[:300])
    b = 5 * np.sin(2 * np.pi * 400 * t[300:800])
    c = 3 * np.sin(2 * np.pi * 600 * t[800:])
    d = np.concatenate((a, b, c), axis=0)
    wavename = 'cgau8'
    totalscal = 256
    fc = pywt.central_frequency(wavename)
    cparam = 2 * fc * totalscal
    scales = cparam / np.arange(totalscal, 1, -1)
    [cwtmatr, frequencies] = pywt.cwt(d, scales, wavename, 1.0 / 1400)
    plt.figure(figsize=(10, 4))
    plt.contourf(t, frequencies, abs(cwtmatr))
    plt.show()


def test1():
    x = np.linspace(0, 1, 1400)
    y = 7 * np.sin(2 * np.pi * 200 * x) + 5 * np.sin(2 * np.pi * 400 * x) + 3 * np.sin(2 * np.pi * 600 * x)
    wavename = 'cgau8'
    totalscal = 256
    # 中心频率
    fc = pywt.central_frequency(wavename)
    cparam = 2 * fc * totalscal
    scales = cparam / np.arange(totalscal, 1, -1)
    [cwtmatr, frequencies] = pywt.cwt(y, scales, wavename, 1.0 / 1400)
    plt.figure(figsize=(8, 4))
    plt.contourf(x, frequencies, abs(cwtmatr))
    plt.show()


if __name__ == '__main__':
    test()

图像为

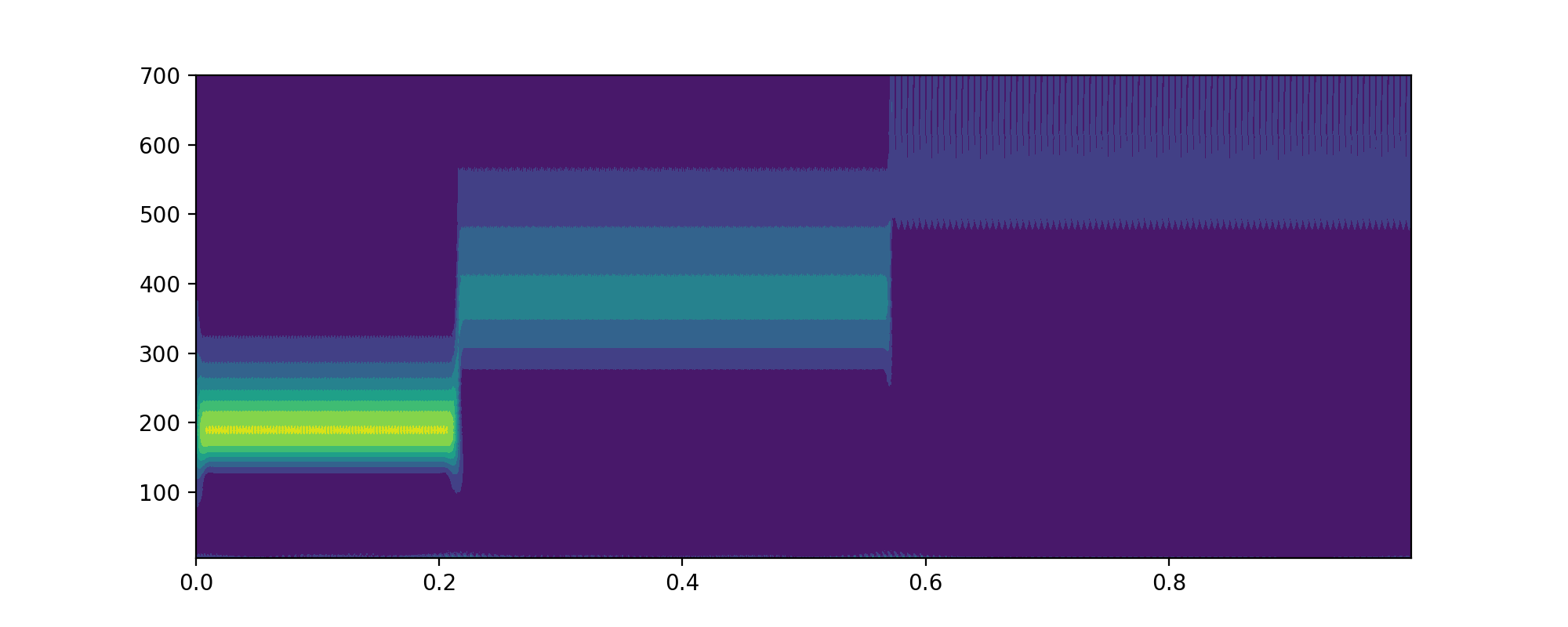
稍微高级一点的代码为

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import matplotlib.pyplot as plt
import numpy as np
import pywt


def test():
    t = np.arange(0, 1.0, 1.0 / 1400)
    data = np.piecewise(t, [t < 1, t < 0.8, t < 0.3],
                        [lambda t: 3 * np.sin(2 * np.pi * 600 * t), lambda t: 5 * np.sin(2 * np.pi * 400 * t),
                         lambda t: 7 * np.sin(2 * np.pi * 200 * t)])
    wavename = 'cgau8'
    totalscal = 256
    fc = pywt.central_frequency(wavename)
    cparam = 2 * fc * totalscal
    scales = cparam / np.arange(totalscal, 1, -1)
    [cwtmatr, frequencies] = pywt.cwt(data, scales, wavename, 1.0 / 1400)
    plt.figure(figsize=(10, 4))
    plt.contourf(t, frequencies, abs(cwtmatr))
    plt.show()


if __name__ == '__main__':
    test()

构图为

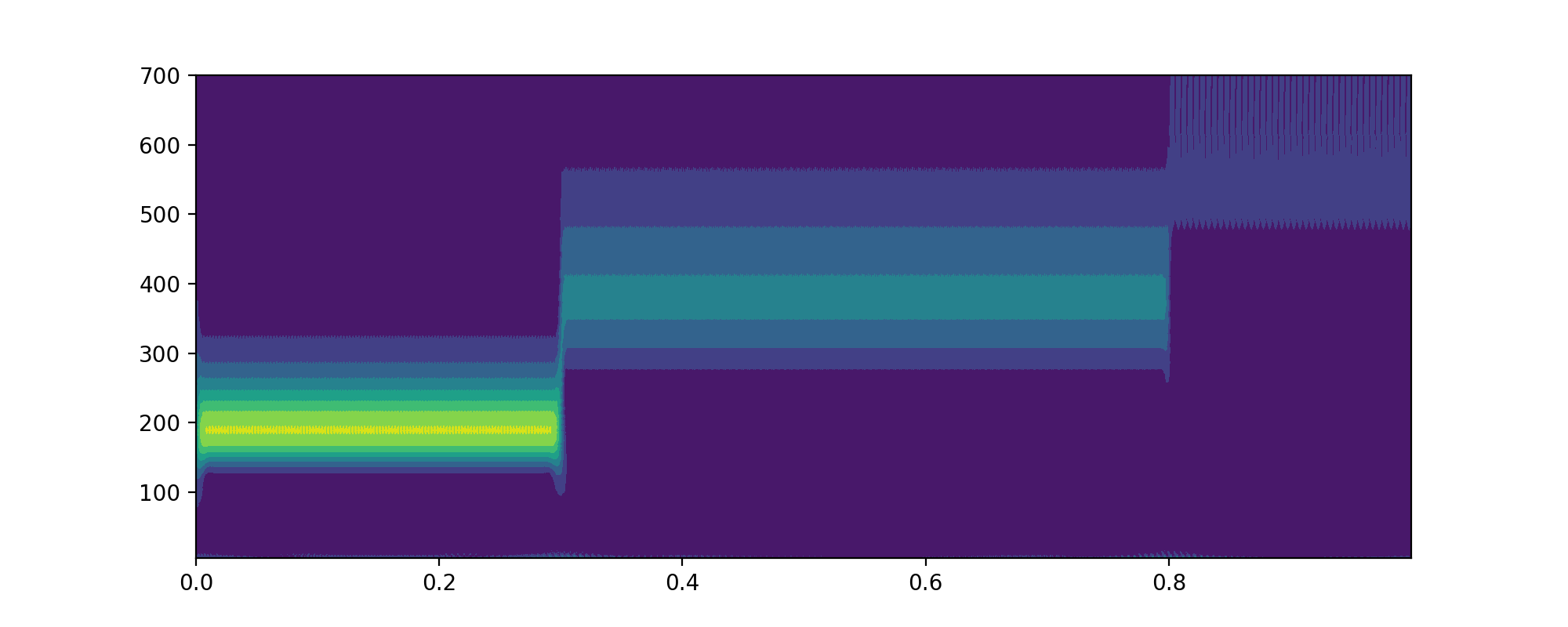
这里要说明的是

np.piecewise

这个方法。

numpy.piecewise(x, condlist, funclist, *args, **kw)
    x： 表示要进行操作的对象
    condlist： 表示要满足的条件列表，可以是多个条件构成的列表
    funclist： 执行的操作列表，参数二与参数三是对应的，当参数二为true的时候，则执行相对应的操作函数

举一个简单的例子

1
2
3
4
5
import numpy as np
x = np.arange(0, 10)
print(x)                                            # [0 1 2 3 4 5 6 7 8 9]
print(np.piecewise(x, [x < 4, x >= 6], [-1, 1]))    # [-1 -1 -1 -1  0  0  1  1  1  1]
# 将元素中小于4的用-1替换掉，大于等于6的用1替换掉，其余的默认以0填充

里面的满足条件是从右向左，也就是先满足 x>= 6 或满足 x < 4

举一个简单的例子

1
2
3
x = np.arange(0, 10)
print(np.piecewise(x, [x < 6, x < 4], [-1, 1])) # [ 1  1  1  1 -1 -1  0  0  0  0]
print(np.piecewise(x, [x < 4, x < 6], [-1, 1])) # [1 1 1 1 1 1 0 0 0 0]

真实的脑电信号例子


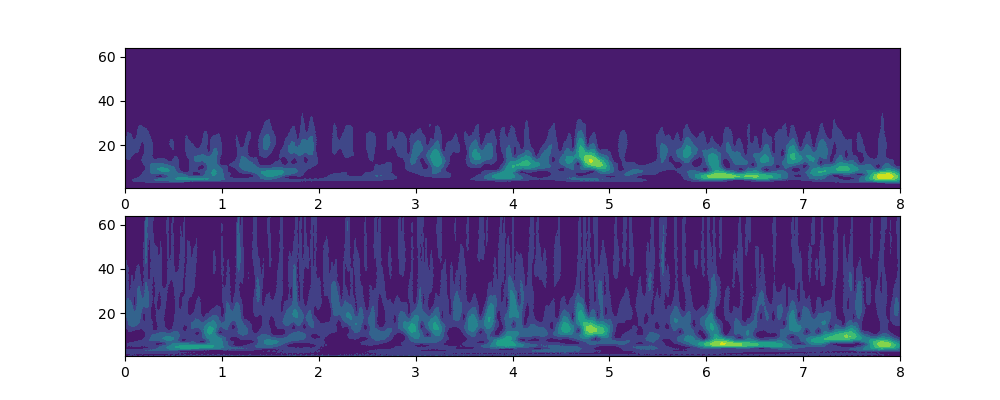
这是用 DECP 数据，然后加了白噪声。

上面是原始数据，下面是加了噪声的数据。这是用 plt.contourf 画的。

如果用 plt.pcolor 画，效果如下

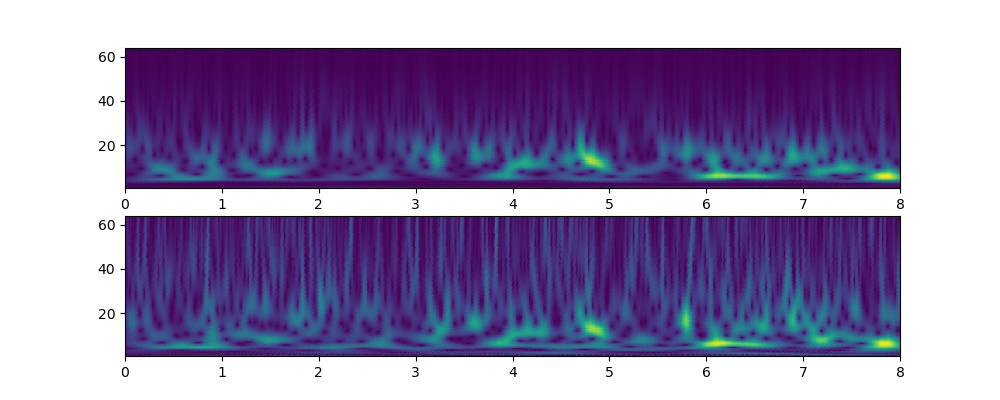
虽然数据都是一套数据，但是，从表现形式来看 plt.contourf 最好。

请我喝杯咖啡吧～