姑苏城外一茅屋，万树梅花月满天

0%

ResNet | 认识残差网络

发表于 更新于 分类于 ， ， ， ， ， ， ， Valine：

这里主要讲残差的基础入门，也就是残差块。


参考资料



什么是残差（residual）？

残差在数理统计中是指实际观察值与估计值（拟合值）之间的差。如果回归模型正确的话， 我们可以将残差看作误差的观测值。

更准确地，假设我们想要找一个 𝑥，使得 𝑓(𝑥)=𝑏 ，给定一个 𝑥 的估计值 $ x_0 $ ，残差（residual）就是 𝑏−𝑓(𝑥0)，同时，误差就是 $ 𝑥−𝑥_0 $。

即使 𝑥 不知道，我们仍然可以计算残差，只是不能计算误差罢了。


什么是残差网络（Residual Networks，ResNets）？


在了解残差网络之前，先了解下面这个问题。

Q1：神经网络越深越好吗？（Deeper is better？）

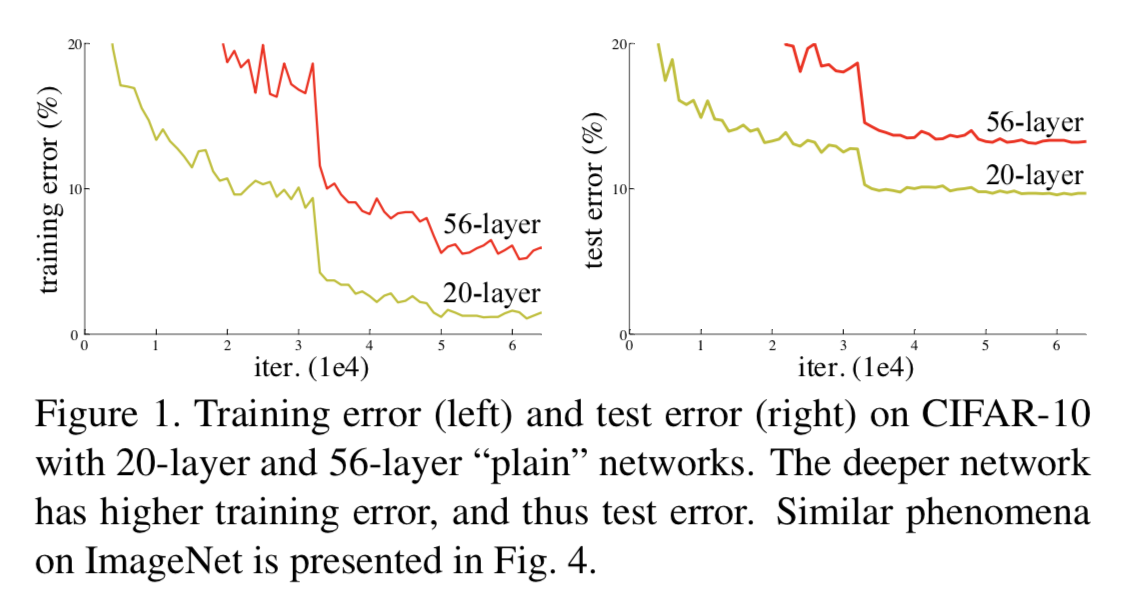
A1：如图所示，在训练集上，传统神经网络越深效果不一定越好。而 Deep Residual Learning for Image Recognition 这篇论文认为，理论上，可以训练一个 shallower 网络，然后在这个训练好的 shallower 网络上堆几层 identity mapping（恒等映射） 的层，即输出等于输入的层，构建出一个 deeper 网络。这两个网络（shallower 和 deeper）得到的结果应该是一模一样的，因为堆上去的层都是 identity mapping。这样可以得出一个结论：理论上，在训练集上，Deeper 不应该比 shallower 差，即越深的网络不会比浅层的网络效果差。但为什么会出现图 这样的情况呢，随着层数的增多，训练集上的效果变差？这被称为退化问题（degradation problem），原因是随着网络越来越深，训练变得原来越难，网络的优化变得越来越难。理论上，越深的网络，效果应该更好；但实际上，由于训练难度，过深的网络会产生退化问题，效果反而不如相对较浅的网络。而残差网络就可以解决这个问题的，残差网络越深，训练集上的效果会越好。（测试集上的效果可能涉及过拟合问题。过拟合问题指的是测试集上的效果和训练集上的效果之间有差距。）

  • plain network指的是没有使用 shortcut connection 的网络

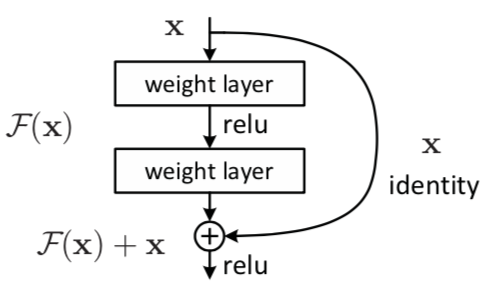
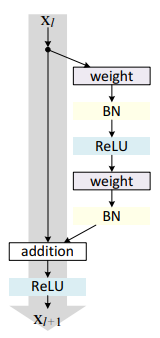
残差网络通过加入 shortcut connections，变得更加容易被优化。包含一个 shortcut connection 的几层网络被称为一个残差块（residual block），如下图所示。（shortcut connection，即图右侧从𝑥 到 ⨁ 的箭头）

而右侧的弧线，通常为

里面的 weight layer 可以根据需求自己规定，这里使用 conv 也就是卷积作为 weight layer。


残差块（residual block）


如上图所示，𝑥 表示输入，𝐹(𝑥) 表示残差块在第二层激活函数之前的输出，即 $ 𝐹(𝑥)=𝑊_2𝜎(𝑊_1𝑥) $，其中 $ 𝑊_1 $ 和 $ 𝑊_2 $ 表示第一层和第二层的权重，𝜎 表示 ReLU 激活函数。（这里省略了 bias）最后残差块的输出是 𝜎(𝐹(𝑥)+𝑥)。

当没有 shortcut connection（即上图右侧从 𝑥 到 ⨁ 的箭头）时，残差块就是一个普通的 2 层网络。残差块中的网络可以是全连接层，也可以是卷积层。设第二层网络在激活函数之前的输出为 𝐻(𝑥)。如果在该 2 层网络中，最优的输出就是输入 𝑥，那么对于没有 shortcut connection 的网络，就需要将其优化成 𝐻(𝑥)=𝑥,对于有 shortcut connection 的网络，即残差块，如果最优输出是 𝑥，则只需要将 𝐹(𝑥)=𝐻(𝑥)−𝑥 优化为 0 即可。后者的优化会比前者简单。这也是残差这一叫法的由来。

上面说的有点弯弯绕绕，还是直接举例子吧。

ps： 当时我这个是为了处理一维信号，所以，可以根据需求来更改

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
# 定义残差块ResBlock
class ResBlock(nn.Module):
    def __init__(self, inchannel, outchannel, stride=1):
        super(ResBlock, self).__init__()
        # 这里定义了残差块内连续的2个卷积层
        self.left = nn.Sequential(
            nn.Conv2d(inchannel, outchannel, kernel_size=(1, 3), stride=stride, padding=(0, 1), bias=False),
            nn.BatchNorm2d(outchannel),
            nn.ReLU(inplace=True),
            nn.Conv2d(outchannel, outchannel, kernel_size=(1, 3), stride=1, padding=(0, 1), bias=False),
            nn.BatchNorm2d(outchannel)
        )
        self.shortcut = nn.Sequential()
        if stride != 1 or inchannel != outchannel:
            # shortcut，这里为了跟2个卷积层的结果结构一致，要做处理
            self.shortcut = nn.Sequential(
                nn.Conv2d(inchannel, outchannel, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(outchannel)
            )

    def forward(self, x):
        out = self.left(x)
        # 将2个卷积层的输出跟处理过的x相加，实现ResNet的基本结构
        out = out + self.shortcut(x)
        out = F.relu(out)

        return out

上面是一个残差块。

left 表示正常的卷积网络。

关于 cnn 的网络计算公式为

这里看一下计算过程，假如说输入的为 (1，1000) 的信号，则第一层 conv 输出的信号为

根据公式第一层卷积为

$$ 输出尺寸 = \frac {1000 - 3 + 2 * 1 }{1} + 1 = 1000 $$

第二层的卷积同样是

$$ 输出尺寸 = \frac {1000 - 3 + 2 * 1 }{1} + 1 = 1000 $$

所以，输出后其数据构造还是 (1,1000)

而往往前面真实的数据为

(N,C,1,1000)

  • N 为 batch_size
  • C 为 channel

shortcut 表示图中右边的弧线，其会把最开始输入的 x 变成和 left 输出的信号变成一样的，即 x 也会变成 (N,C,1,1000)

假如说， left 的输出为 N,C,1,1000 shortcut 的输出为 N,C,1,1000 ，那么，两者相加是多少？

是

N,C,1,1000

最终，我们是讲 1，1000 中的值，进行 N ，C 匹配想加。

所以，两个相加得到的值可能会超过 1 ，所以，两者想加完之后，会进行一个 relu

其实残差只是一个思想，把前几层的数值添加到后几层中，使得网络结构可以更深。

所以，我们可以对残差块进行一个修改。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
# 定义残差块ResBlock
class ResBlock(nn.Module):
    def __init__(self, inchannel, outchannel, stride=1):
        super(ResBlock, self).__init__()
        # 这里定义了残差块内连续的2个卷积层
        self.left = nn.Sequential(
            nn.Conv2d(inchannel, outchannel, kernel_size=(1, 3), stride=stride, padding=(0, 1), bias=False),
            nn.BatchNorm2d(outchannel),
            nn.ReLU(inplace=True),
            nn.Conv2d(outchannel, outchannel, kernel_size=(1, 3), stride=1, padding=(0, 1), bias=False),
            nn.BatchNorm2d(outchannel)
        )

    def forward(self, x):
        shortcut = self.left(x)
        # 将2个卷积层的输出跟处理过的x相加，实现ResNet的基本结构
        out = out + shortcut
        out = F.relu(out)

        return out

这里是直接将 x 添加到输出层了。

现在的残差块相加都是 (N,C,1,1000) 但是，我觉得，我们也可以这样相加

(N,C,1,1000) + (N,C,1,1000) = (N,2C,1,1000)

而且，我觉得这样更加合理。相关的代码在这里不写了。

另外，我们需要注意的是

假设尺寸变化，那么相加需要满足图像大小相同才能添加。

假设，最后得出的图像不同，那该如何写代码？

在这里，建议参考，我下面的博客，以后，我也会专门对照这个代码写一下 resnet 的代码

上面的博文主要看特征融合那一栏。

里面的思想有

  • (N,C,1,1000) + (N,C,1,1000) = (N,2C,1,1000)
  • 解决尺寸不匹配问题

残差网络


残差网络主要是讲残差块组合在一起。

只见看一下代码吧。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
import torch
import torch.nn as nn
import torch.nn.functional as F
import numpy as np


# 定义残差块ResBlock
class ResBlock(nn.Module):
    def __init__(self, inchannel, outchannel, stride=1):
        super(ResBlock, self).__init__()
        # 这里定义了残差块内连续的2个卷积层
        self.left = nn.Sequential(
            nn.Conv2d(inchannel, outchannel, kernel_size=(1, 3), stride=stride, padding=(0, 1), bias=False),
            nn.BatchNorm2d(outchannel),
            nn.ReLU(inplace=True),
            nn.Conv2d(outchannel, outchannel, kernel_size=(1, 3), stride=1, padding=(0, 1), bias=False),
            nn.BatchNorm2d(outchannel)
        )
        self.shortcut = nn.Sequential()
        if stride != 1 or inchannel != outchannel:
            # shortcut，这里为了跟2个卷积层的结果结构一致，要做处理
            self.shortcut = nn.Sequential(
                nn.Conv2d(inchannel, outchannel, kernel_size=1, stride=stride, bias=False),
                nn.BatchNorm2d(outchannel)
            )

    def forward(self, x):
        out = self.left(x)
        # 将2个卷积层的输出跟处理过的x相加，实现ResNet的基本结构
        out = out + self.shortcut(x)
        out = F.relu(out)

        return out


class ResNet(nn.Module):
    def __init__(self, ResBlock, num_classes=1000):
        super(ResNet, self).__init__()
        self.inchannel = 64
        self.conv1 = nn.Sequential(
            nn.Conv2d(1, 64, kernel_size=(1, 3), stride=1, padding=(0, 1), bias=False),
            nn.BatchNorm2d(64),
            nn.ReLU()
        )
        self.layer1 = self.make_layer(ResBlock, 64, 2, stride=1)
        self.layer2 = self.make_layer(ResBlock, 128, 2, stride=2)
        self.layer3 = self.make_layer(ResBlock, 256, 2, stride=2)
        self.layer4 = self.make_layer(ResBlock, 512, 2, stride=2)
        self.fc = nn.Linear(15872, num_classes)

    # 这个函数主要是用来，重复同一个残差块
    def make_layer(self, block, channels, num_blocks, stride):
        strides = [stride] + [1] * (num_blocks - 1)
        layers = []
        for stride in strides:
            layers.append(block(self.inchannel, channels, stride))
            self.inchannel = channels
        return nn.Sequential(*layers)

    def forward(self, x):
        # 在这里，整个ResNet18的结构就很清晰了
        out = self.conv1(x)
        out = self.layer1(out)
        out = self.layer2(out)
        out = self.layer3(out)
        out = self.layer4(out)
        out = F.avg_pool2d(out, kernel_size=(1, 4))
        out = out.view(out.size(0), -1)
        out = self.fc(out).reshape((out.shape[0], 1, 1, 1000))
        return out

这里面代码都非常好理解，在这里，主要是对 make_layer 这个函数做解释。

1
2
3
4
5
6
7
8
# 这个函数主要是用来，重复同一个残差块
def make_layer(self, block, channels, num_blocks, stride):
    strides = [stride] + [1] * (num_blocks - 1)
    layers = []
    for stride in strides:
        layers.append(block(self.inchannel, channels, stride))
        self.inchannel = channels
    return nn.Sequential(*layers)

make_layer 指的是最终 resnet 是几层网络，比如，有 resnet-18,resnet-32,resnet-50 等。

像这个网络结构就是 resnet-18。

关于为什么是 restnet-18 请参考我下面的博文。

请我喝杯咖啡吧～