如题。
有人说,导数是瞬时变化率。这个说法究竟对不对呢,请看下面的解答。
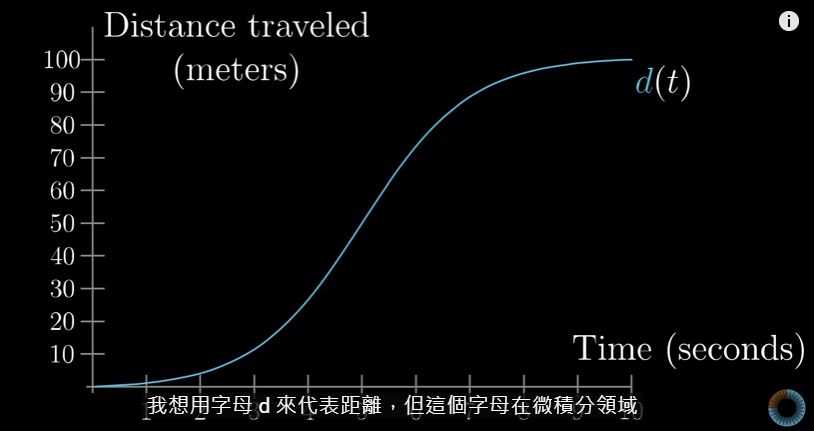
假设,有一辆车,它初始是加速的,到达某一时间点的时候,它开始减速,直到速度为 0,一共行驶了 3 分钟。图像如下:
其中横坐标是时间,竖坐标是距离。
我们的疑问是,如何计算汽车在某一时间点的速度。
其实,汽车在某一个时间点是无法计算速度的,就好像你在某一时间点给汽车拍一张照片,但是我们无法从照片中得知汽车的速度到底是多少?
OK,那我们如何计算这个瞬时速度呢?
假设我们要计算某一时间段的速度,我们很容易的便会想到用距离除以时间。
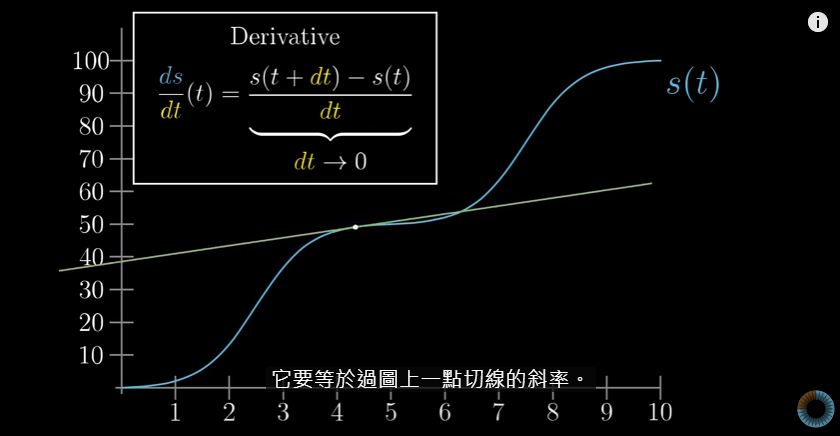
v = d / t那如果,我们将时间变得尽可能小呢?我们将尽可能小的时间成为 dt
我们就会发现原来的瞬时速度,随着 dt 越来越小,就变成了某一点的斜率。
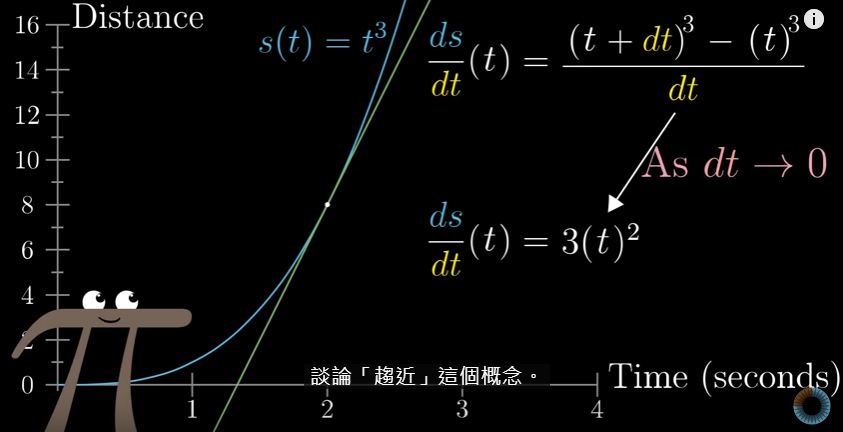
当然,我们想更加具体的举一个例子,比如,我想计算一下,在时间点 2 上的车的瞬时速度。
如下图所示。
经过将图中的式子化简,( dt 因为无限的趋向于零,所以凡是和 dt 相乘的都可以看作零)
导数从本质上讲只是关注着某一个量(dx)的微小变化,以及与之关联的另一个量(dy)的微小变化。