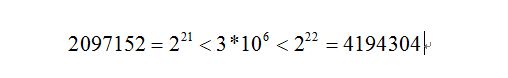Genetic Algorithms(GA) 是遗传算法,这是一个非常有意思的算法,我将会详细分析这个算法。
基本原理
自然界
关于具体术语我就不说了,我先用自然界的遗传入手。按照达尔文的进化论来说,适者生存。也就是说越适应环境的生物,生存几率越大。
话语虽短,但是却传达了几点非常重要的信息,第一,必须先有母群和父群才能进化,也就是进化是在后代不断地迭代中产生。第二,进化就是好的性状更加适应于环境,而这个性状的遗传来自于父群和母群,第三,由于环境恶劣,导致不适应环境的性状被淘汰,而适应环境的性状被保留,并且由于适应环境的性状被保留的越多,拥有这个性状的种群数量也就越多,所以,最后优等种群成为一种常态。
也就是说适者生存包括,性状遗传,环境淘汰,种群扩大这些概念。
但是,我们也知道由于遗传的过程中,基因在某种情况下不会按照父群和母群遗传,而是基因突变成另外一个个体,所以,这个个体可能会变的极为优秀,也有可能会直接夭折。
计算机界
20世纪70年代,由 Hollyand 教授,首先提出 GA 算法,在这个算法中提出模拟自然的遗传。
还是先举自然地例子。
在一片绵延的山脉中,有一群随机分布的袋鼠,它们以群居的方式居住在山脉的各个地方,这时,谷底突然弥漫出一种毒雾。
毒雾从谷底向山顶蔓延,而袋鼠也有自己的生活方式,一种是会迁居到山脚,一种是不动,另一种是跳到山顶。
由于拥有毒素的原因,迁居到山脚的袋鼠开始相继死亡,而越往上走的袋鼠反而会活的越多,最终,剩下的袋鼠都喜欢往上走。
那有没有具体的数学例子呢?
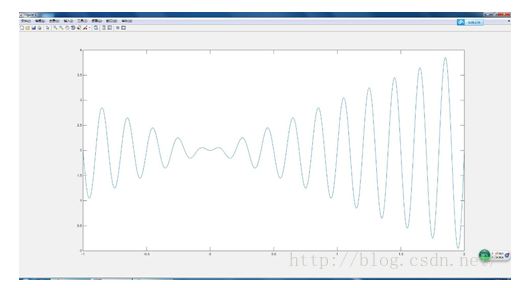
看下面的函数
将这个函数画出图像我们就能得出
首先我们知道函数的定义域是 [-1,2] 相当于物种是袋鼠,这是个限制,我们就是要找那个数能得到函数的最大值。
假设我们随机初始化一部分数,这些数分布在图像的各个地方,我们通过比对的方式,将函数值小的数进行消灭,然后,我们将函数值对应大的数进行交叉(也就是一半的二进制来自于一个数,另一半的二进制来自于另一个数),通过不断地繁衍淘汰,最终我们的数是越来越向顶峰靠近。
原理很简单,但是涉及到很多难点。
如何编码函数值?
交叉究竟按照那种方式交叉?
数的存活率应该怎么安排?
变异又将按照什么方式进行?
淘汰机制是什么?下面我将围绕着这些问题来进行深入的研究。
GA 的编码
遗传算法使用固定长度的二进制符号串来表示群体中个体。
即基因是由二进制组成。
01000110
染色体长度为 8如果一个参数的取值范围是 [min,max] ,如果我们用长度为 λ ,那么我们一共可以表示 2 ^ λ 个。
如果我们需要精确到某一位,也就是精度限制,假设我们的精度要求是 δ
公式如下:
具体例子如下,我们要精确到 6 位小数,由于定义域是 [-1,2] ,也就是长度是 2 + 1 = 3。
则在区间内我们至少分为 3 * 10 ^ 6 个等分。
又因为
所以编码的二进制至少需要 22 位。
OK,现在我们编码算是糊弄过去了,那么如何解码?给你一段二进制代码,如何将这段二进制解码成定义域中的数值?
看如下公式:
看不懂对吧,很正常,这是中国人自以为是的技能,将简单问题复杂化,用来彰显自己学术水平牛逼。
所以,还是举一个例子。
将一段二进制代码映射到对应区间中,主要是经过两个步骤。
1. 讲一个二进制代码转化为十进制数
2. 将这个十进制数转化为对应区间的实数如,二进制串: 1000101110110101000111 ,表示实数值为 0.637197
OK,到这里,正如原文中所说,对于基因的编码和解码我们应该不成问题了。
随机
我们初始化的种群一定是随机的,并且要确保分布在定义域的各个地方。
换句话说,群体的分布规模越大,群体中个体的多样性越多,算法陷入局部最优解的可能性就越小。
那么究竟多少个群体才算是好群体?怎么分布才算是好分布?
在二进制编码下,为了满足隐并行性,群体个体数只要设定为 2 ^(L/2) 其中 L 是个体串长度,但这个数通常比较大,所以一般个体数为几十到几百。
淘汰机制与适应度[物竞天择]
物竞
就好像毒雾会杀死袋鼠,我们也应该有一种淘汰机制将不好的数据杀死,然后保留好的数据。
群体进化的过程就是以群体中个体的适应度为依据,通过反复迭代过程,不断地寻求出适应度较大的个体,最终得到问题的最优解或近似最优解。
所以,上述的讲解告知,适应度是一个正数或者零,但不是负数。
但是我们对于一个问题的求解就是寻求这个问题的最优解,也就是通过和最优解的比对我们知道其存活率如何。
换句话说,我们求一种数据的最大值,在每一次迭代的过程中,最终个体求解的数越大其存活率也就越高。
但是,单一的利用原函数并不能满足我们的要求,因为原函数最终得值有负有正,所以,单纯的求解满足不了适应度非负的前提,所以,我们要做一些变换。


我们如何定义每个个体的适应度呢?
我们事先要了解两个现象。
第一,在遗传初期,通常会出现一些超长个体,若按比例选择策略,这些异常个体在种群中会占很大的比例,导致未成熟收敛。显然,因为异常个体的数量太多,导致最后整体都向他们变化,将导致局部最优解。
第二,如果随着个体不断地繁衍,导致个体与个体之间都近似相似,使得整个种群的进化力度趋近于零,导致无法进化成最佳个体,从而使得优化过程趋于无目标的随机搜索过程。
下面将是解决方案,但是,我没懂,因为这节课我因为有很重要的事,逃了。。。

改天问一下老师。。。
天择
我们知道物种之间相互竞争,但是我们如何制定淘汰机制来选择合适的种群呢?
最常用的方法就是选择算子。
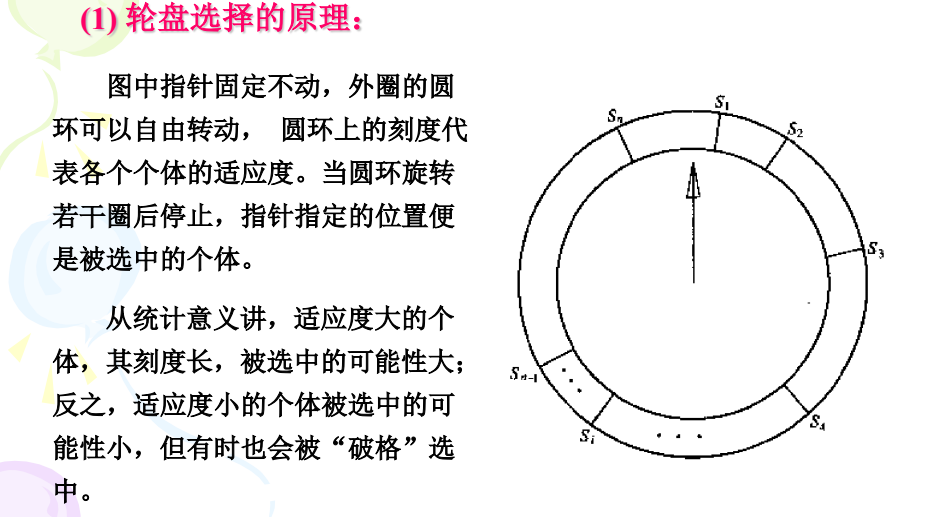
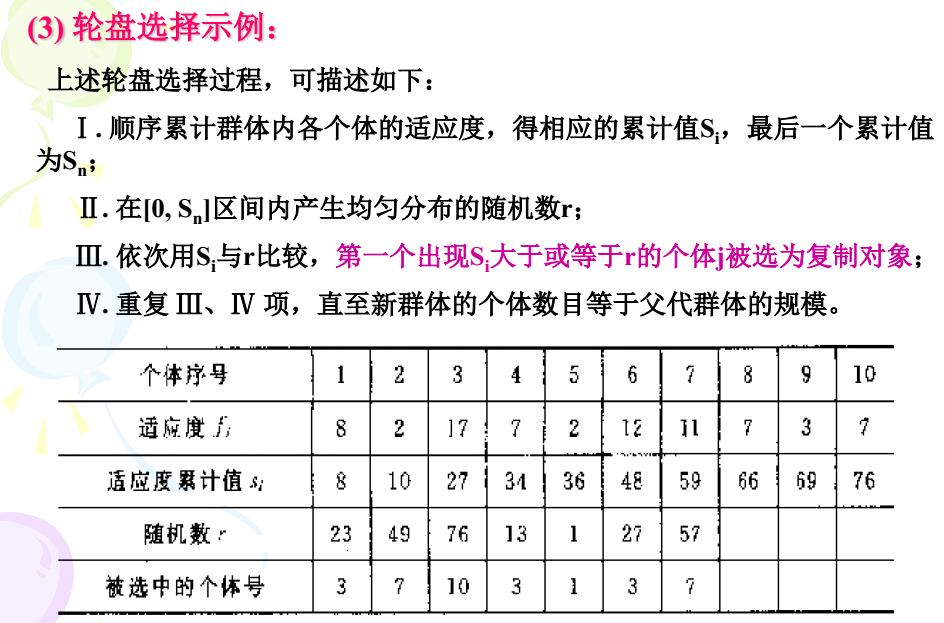
选择算子:只个体被选中并遗传到下一代群体的概率与该个体的适应度大小成正比一般执行选择算子的手段是轮盘选择,精英选择,稳态选择。

遗传变异
嘿嘿嘿,最让人羞羞的代码来了,如何进行交配产生下一代。QvQ
单点交叉算子



基本位变异算子
这个算法是讲变异的,富人靠科技,穷人靠变异。


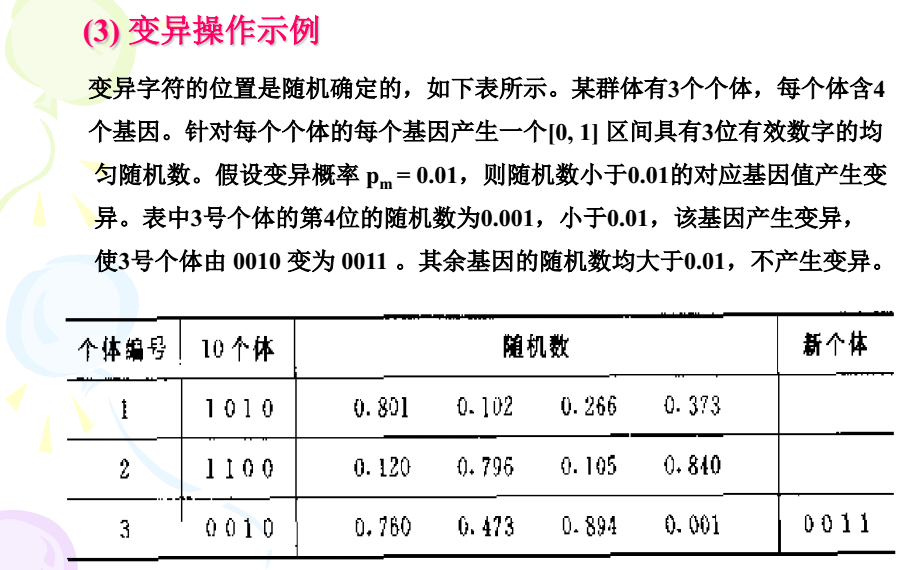
用数学的角度看 GA
术语讲解
个体:是由 0,1 组成的编码串
模式:是由 0,1,* 组成的编码串,其中 * 是通配符,可以是 1,也可以是 0
*1101 代表 2 个个体 11101 01101模式阶:表示模式中已经有明确含义字符的个数
*01*11 的模式阶为 4
模式阶用 O() 表示
即: O(*01*11) = 4阶次越低表示模式的概括能力越强,个数越多,反之相反。
模式的定义长度:指模式中第一个和最后一个具有明确含义字符之间的距离,记作 ξ() (OK,不是这个符号,因为那个符号我找不到了。。。罪过)
ξ(011*1**) = 4值得让人注意的是,他们的下标也是从 0 开始标注,所以,长度通常为正常人逻辑长度 -1
模式总数:其实这就是一个简单的数学,为 3 ^ λ (3 代表 0 1 *)
种群含有的模式数为: 2^λ - M * 2^λ 其中 M 为规模 λ 为长度
假设地 t 次迭代时,种群 P 有 M 个个体,其中 m 个个体属于模式 s,记作 m(s,t)
数学推导
适应度和被选中的概率

第 t 代产生了,其中有一个种群是 s ,那么第 t + 1 代中,种群 s 的数目如下公式计算:
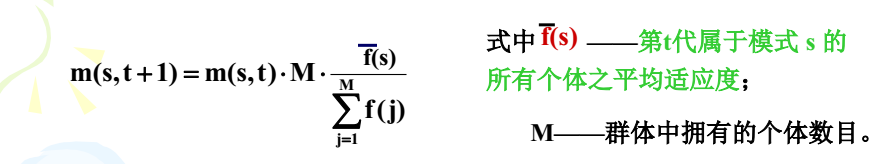
由于公式难写,所以,下面的公式推导我大都采用截图,必要的时候我会给祥加说明,非我懒惰,只是实在是找不到特殊符号的编码。


这个公式说明下一代模式 s 的种群取决于种群 s 的平均适应度和全部个体平均适应度之比。且只有这两个的比大于 1 ,种群 s 的数目才能增加,否则数目减小。
正好符合优胜略汰的道理。


下面仅仅是推导单点交叉。

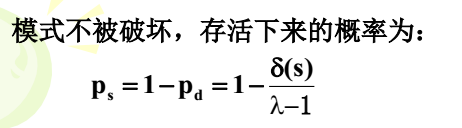
我在别的地方找的一个图片,道理是相通的,所以我就不过多的陈述了


也就是说,模式的长度越长,越容易被破坏。
变异模式下的推导


上述公式即为模式定理,适应度高于群体平均适应度的,长度较短,低阶的模式在遗传算法的迭代过程中将按照指数规律增长。
建筑块假说
这个假说其实并没有太大的用,但是也可能是我理解的不深。。。
我们都知道一个复杂问题的最优解,是由多个最优解参数求得的,就好像基因假说,一个完美的种群,它的所属基因也是完美的。
建筑块假说将基因比作一个个的积木,想要得到最好的建筑,只需要将最好的积木项目叠加即可。
隐含并行性
模式存活的最小长度

这张图有几点需要解释一下,第一,ε 是 0 和 1 之间的数,代表很小的数,第二,图片中的 l 和 λ 是一个含义。
个体编码串中拥有存活长度的模式数目
下面我都是截图给出,讲道理,为什么会有隐含,我是看不太懂。



遗传算法的特点总结
(1)遗传算法从问题解的串集开始搜索,而不是从单个解开始。这是遗传算法与传统优化算法的极大区别。传统优化算法是从单个初始值求最优解的;容易误入局部最优解。遗传算法从串集开始搜索,覆盖面大,利于全局择优。
(2)遗传算法同时处理群体中的多个个体,即对搜索空间中的多个解进行评估,减少了陷入局部最优解的风险,同时算法本身易于实现并行化。
(3)遗传算法基本上不用搜索空间的知识或其他辅助信息,而仅用适应度函数值来评估个体,在此基础上进行遗传操作。适应度函数不仅不受连续可微的约束,而且其定义域可以任意设定。这一特点使得遗传算法的应用范围大大扩展。
(4)遗传算法不是采用确定性规则,而是采用概率的变迁规则来指导他的搜索方向。
(5)具有自组织、自适应和自学习性。遗传算法利用进化过程获得的信息自行组织搜索时,适应度大的个体具有较高的生存概率,并获得更适应的基因结构。