这是深度学习经常会遇到的问题。
参考资料
原因
从反向传播本身
我们以一个简单的 DNN 网络为例。
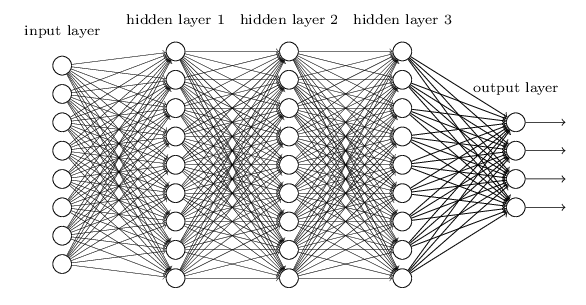
而这种问题为何会产生呢?以下图的反向传播为例(假设每一层只有一个神经元且对于每一层 $ y_i = \sigma (z_i) = \sigma (w_i * x_i+ b_i) $,其中 $ \sigma $ 为 sigmoid函数)

可以推导出
对于四个隐层来说,其更新速度,如下
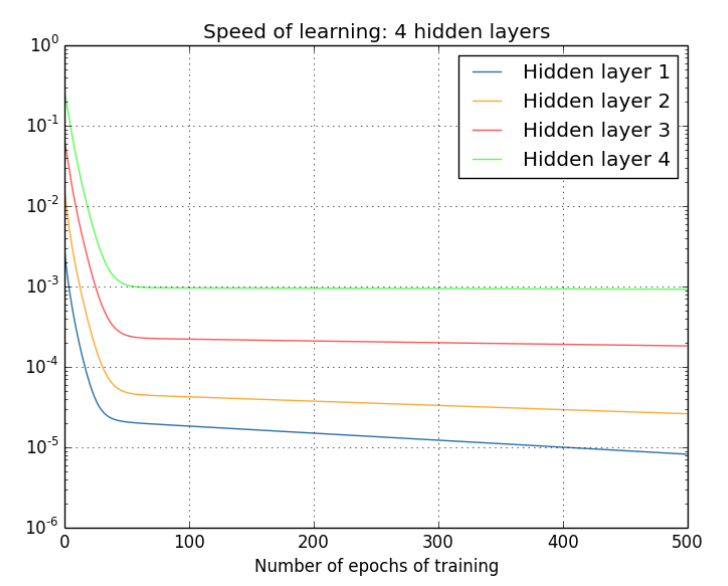
从深层网络角度来讲,不同的层学习的速度差异很大,表现为网络中靠近输出的层学习的情况很好,靠近输入的层学习的很慢,有时甚至训练了很久,前几层的权值和刚开始随机初始化的值差不多。因此,梯度消失、爆炸,其根本原因在于反向传播训练法则,属于先天不足。
从激活函数的角度来看
sigmod

左图是 sigmoid 的损失函数图,右边是其导数的图像,如果使用 sigmoid 作为损失函数,其梯度是不可能超过 0.25 的,这样经过链式求导之后,很容易发生梯度消失。
tanh
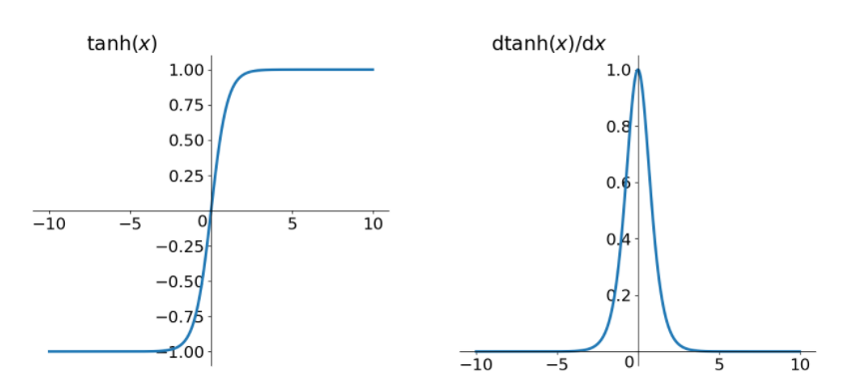
同理,tanh 作为激活函数,它的导数图如下,可以看出,tanh 比 sigmoid 要好一些,但是它的导数仍然是小于1的。
总结
我们把梯度下降的先天不足和激活函数结合在一起看。
以
为例,激活函数是 sigmod。
可见,$ \sigma ^‘{(x)} $的最大值为 0.25 ,而我们初始化的网络权值 $ |w| $通常都小于 1,因此$ |\sigma ^‘{(z)w}| <= 0.25 $,因此对于上面的链式求导,层数越多,求导结果$ \alpha C \over \alpha b_1 $
越小,因而导致梯度消失的情况出现。
这样,梯度爆炸问题的出现原因就显而易见了,即$ |\sigma ^‘{(z)w}| > 1 $,也就是 $ w $ 比较大的情况。但对于使用 sigmoid 激活函数来说,这种情况比较少。因为$ \sigma ^‘{(x)} $的大小也与 $ |w| $有关($ z = wx + b $),除非该层的输入值 $ x $ 在一直一个比较小的范围内。
其实梯度爆炸和梯度消失问题都是因为网络太深,网络权值更新不稳定造成的,本质上是因为梯度反向传播中的连乘效应。
解决方案
- 预训练加微调
- 梯度剪切、正则
- relu、leakrelu、elu等激活函数
- batchnorm
- 残差结构
- LSTM
预训练加微调
此方法来自 Hinton 在2006年发表的一篇论文,Hinton 为了解决梯度的问题,提出采取无监督逐层训练方法,其基本思想是每次训练一层隐节点,训练时将上一层隐节点的输出作为输入,而本层隐节点的输出作为下一层隐节点的输入,此过程就是逐层“预训练”( pre-training );在预训练完成后,再对整个网络进行“微调”(fine-tunning)。Hinton在训练深度信念网络(Deep Belief Networks中,使用了这个方法,在各层预训练完成后,再利用BP算法对整个网络进行训练。此思想相当于是先寻找局部最优,然后整合起来寻找全局最优,此方法有一定的好处,但是目前应用的不是很多了。
梯度剪切、正则
梯度剪切这个方案主要是针对梯度爆炸提出的,其思想是设置一个梯度剪切阈值,然后更新梯度的时候,如果梯度超过这个阈值,那么就将其强制限制在这个范围之内。这可以防止梯度爆炸。
注:在WGAN中也有梯度剪切限制操作,但是和这个是不一样的,WGAN限制梯度更新信息是为了保证lipchitz条件。
另外一种解决梯度爆炸的手段是采用权重正则化(weithts regularization)比较常见的是 l1正则,和 l2正则,在各个深度框架中都有相应的 API 可以使用正则化。
正则化是通过对网络权重做正则限制过拟合,仔细看正则项在损失函数的形式:
$$ Loss=(y-W^Tx)^2+ \alpha ||W||^2 $$
其中,$ \alpha $ 是指正则项系数,因此,如果发生梯度爆炸,权值的范数就会变的非常大,通过正则化项,可以部分限制梯度爆炸的发生。
注:事实上,在深度神经网络中,往往是梯度消失出现的更多一些。
relu、leakrelu、elu等激活函数
Relu
$$ Relu(x) = max(x,0) = \begin{cases}
0,x<0 \\
x,x>0
\end{cases} $$

从上图中,我们可以很容易看出,relu 函数的导数在正数部分是恒等于 1 的,因此在深层网络中使用 relu 激活函数就不会导致梯度消失和爆炸的问题。
relu 的主要贡献在于:
- 解决了梯度消失、爆炸的问题
- 计算方便,计算速度快
- 加速了网络的训练
同时也存在一些缺点:
- 由于负数部分恒为
0,会导致一些神经元无法激活(可通过设置小学习率部分解决) - 输出不是以
0为中心的
尽管 relu 也有缺点,但是仍然是目前使用最多的激活函数。
leakrelu
leakrelu 就是为了解决 relu 的 0 区间带来的影响,其数学表达为:
$$ leakrelu=max(k*x,x) $$
其中 k 是 leak 系数,一般选择 0.01 或者 0.02,或者通过学习而来。

leakrelu 解决了 0 区间带来的影响,而且包含了 relu 的所有优点。
elu
$$
\begin{cases}
x,ifx > 0 \\
\alpha(e^x - 1),otherwise
\end{cases}
$$
elu 激活函数也是为了解决 relu 的0区间带来的影响。
其函数及其导数数学形式为
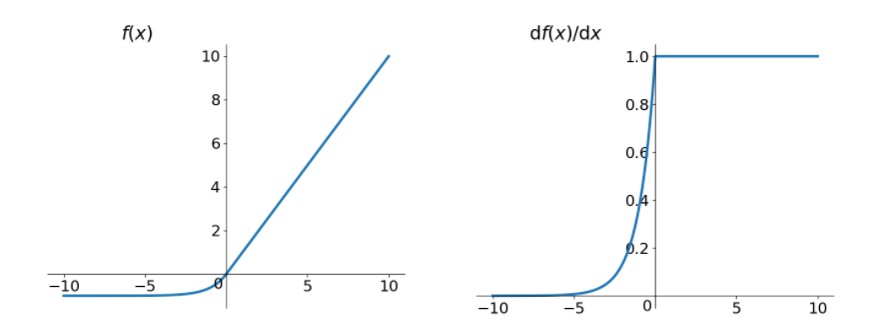
但是 elu 相对于 leakrelu 来说,计算要更耗时间一些。
batchnorm
Batchnorm 是深度学习发展以来提出的最重要的成果之一了,目前已经被广泛的应用到了各大网络中,具有加速网络收敛速度,提升训练稳定性的效果,Batchnorm 本质上是解决反向传播过程中的梯度问题。batchnorm全名是batch normalization,简称BN,即批规范化,通过规范化操作将输出信号x规范化保证网络的稳定性。
具体的 batchnorm 原理非常复杂,你可以参考我下面的博文:
此部分大概讲一下 batchnorm 解决梯度的问题上。具体来说就是反向传播中,经过每一层的梯度会乘以该层的权重,举个简单例子:
正向传播中$ f_2=f_1(w^T*x+b) $,那么反向传播中,$\frac {\partial f_2}{\partial w}=\frac{\partial f_2}{\partial f_1}x $,反向传播式子中有 $ x $ 的存在,所以 $ x $的大小影响了梯度的消失和爆炸,batchnorm就是通过对每一层的输出规范为均值和方差一致的方法,消除了x xx带来的放大缩小的影响,进而解决梯度消失和爆炸的问题,或者可以理解为BN将输出从饱和区拉倒了非饱和区。
残差结构
关于残差的知识点,你可以参考我的博文
事实上,就是残差网络的出现导致了image net比赛的终结,自从残差提出后,几乎所有的深度网络都离不开残差的身影,相比较之前的几层,几十层的深度网络,在残差网络面前都不值一提,残差可以很轻松的构建几百层,一千多层的网络而不用担心梯度消失过快的问题,原因就在于残差的捷径( shortcut )部分。
LSTM
LSTM 全称是长短期记忆网络(long-short term memory networks),是不那么容易发生梯度消失的,主要原因在于 LSTM 内部复杂的“门”(gates),LSTM通过它内部的“门”可以接下来更新的时候“记住”前几次训练的”残留记忆“。
ps: 我一直理解不了 RNN 相关的网络,所以,在这里暂时不补充了。
