姑苏城外一茅屋，万树梅花月满天

0%

算法 | 斐波那契与记忆性

发表于 更新于 分类于 ， ， Valine：

斐波那契数列是一系列的数字，除了第一个和第二个之外的任何数字都是其前两个数之和：

0, 1, 1, 2, 3, 5, 8, 13, 21, …

序列中第一个斐波那契数的值是0。第四个斐波那契数的值是2。因此，要得到序列中任意斐波那契数n的值，可以使用以下公式

fib(n) = fib(n - 1) + fib(n - 2)

参考资料



第一次递归尝试


上述计算斐波那契数列中值的公式是一种伪代码形式，可以简单地转换成 Python 递归函数（递归函数是自我调用的函数）。这种机械转换将作为我们编写斐波那契数列的第一次尝试。

程序清单1 fib1.py

1
2
3
4
5
6
def fib1(n: int) -> int:
	return fib1(n - 1) + fib1(n - 2)


if __name__ == "__main__":
	print(fib1(5))

如果我们尝试运行 fib1.py，程序会产生错误：

RecursionError: maximum recursion depth exceeded

其结果是 fib(1) 将一直运行下去，而不返回最终结果。每次调用 fib1() 都会导致另外两次调用 fib1() 而不会结束。我们将这种情况称为无限递归（infinite recursion），如图1所示，这类似于无限循环。


利用初始条件


值得注意的是，在运行 fib1() 之前，Python 环境没有任何迹象表明它存在问题。程序员有责任避免无限递归，而不是依靠编译器或解释器。无限递归的原因是我们未指定初始条件。在递归函数中，将初始条件作为停止点。

在斐波那契函数的情况下，序列的前两个值（0，1）是特殊情况，它们都不是它们之前两个值之和。让我们将它们作为初始条件。

程序清单2 fib2.py

1
2
3
4
5
6
7
8
9
def fib2(n: int) -> int:
	if n < 2:    # base case
		return n
	return fib2(n - 1) + fib2(n - 2)    # recursive case


if __name__ == '__main__':
	print(fib2(5))
	print(fib2(10))

尝试使用一些小值，可以成功调用 fib2() 并返回正确的结果。

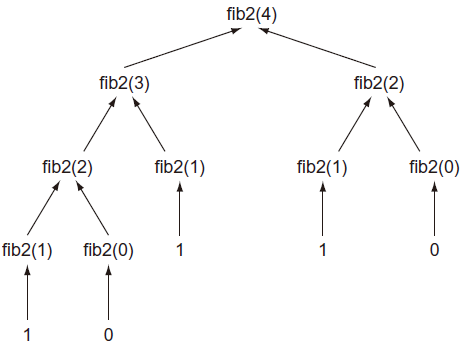
不要试着调用 fib2(50)，执行永远不会完成！为什么？如图2所示，每次调用 fib2() 都会通过递归调用 fib2(n - 1) 和 fib2(n - 2) 产生2个另外 fib2() 调用。换句话说，调用树呈指数增长。例如，调用 fib2(4) 会产生：

fib2(4) -> fib2(3), fib2(2)
fib2(3) -> fib2(2), fib2(1)
fib2(2) -> fib2(1), fib2(0)
fib2(2) -> fib2(1), fib2(0)

fib2(1) -> 1
fib2(1) -> 1
fib2(1) -> 1
fib2(0) -> 0
fib2(0) -> 0

如果计算（在代码中添加一些 print 调用），你会发现，仅仅为了计算第4个元素就需要9次调用！计算第5个元素需要15次调用，计算第10个元素需要177次调用，计算第20元素需要21,891次调用。程序需要优化。


记忆化拯救世界


记忆化（memoization）是一种在计算完成后，存储计算结果的技术。这样当再次需要它们时，仅需要查找它们，而不是二次（或成百上千次）计算它们。

让我们利用 Python 字典来实现记忆化，以创建新的斐波那契函数。

程序清单3 fib3.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
from typing import Dict


memo: Dict[int, int] = {0: 0, 1: 1}    # base cases

def fib3(n: int) -> int:
    if n not in memo:
        memo[n] = fib3(n - 1) + fib3(n - 2)    # memoization
    return memo[n]


if __name__ == '__main__':
    print(fib3(5))
    print(fib3(50))

现在，可以安全地调用 fib3(50) 了。调用 fib3(20) 只会导致 fib3() 被调用39次，而调用 fib2(20) 会导致 fib2() 调用21891次。memo 中预先填充了0和1的初始条件，从而避免了复杂的 if 语句。

这个是真的牛逼，亮点有下面几个

  • 使用 dict 来暂存数值
    • 我觉得能成立的前提是 key 很好获取
  • dict 里面有返回条件

自动记忆化


fib3() 可以进一步简化。Python 有一个内置装饰器，可以自动记忆任何函数。在 fib4() 中，除了使用了装饰器 @functools.lru_cache()，其他的代码与 fib2() 中的完全相同。每次使用新参数执行 fib4() 时，装饰器都会缓存返回值。之后使用相同参数调用 fib4() 时，将从缓存中取出该参数之前的返回值。

程序清单4 fib4.py

1
2
3
4
5
6
7
8
9
10
11
12
13
from functools import lru_cache


@lru_cache(maxsize=None)
def fib4(n: int) -> int:    # same definition as fib2()
    if n < 2: # base case
        return n
    return fib4(n - 2) + fib4(n - 1) # recursive case


if __name__ == '__main__':
    print(fib4(5))
    print(fib4(50))

请注意，我们能够立即计算出 fib4(50)，即使函数的主体与 fib2() 中的相同。@lru_cache 的 maxsize 属性表示，缓存它正在装饰的函数的调用次数。将其设置为 None 表示没有限制。


迭代


还有一个更高性能的选择，即，用老式的迭代方法解决斐波纳契问题。

程序清单5 fib5.py

1
2
3
4
5
6
7
8
9
10
11
12
def fib5(n: int) -> int:
    if n == 0: return 0    # special case
    last: int = 0    # initially set to fib(0)
    next: int = 1    # initially set to fib(1)
    for _ in range(1, n):
        last, next = next, last + next
    return next


if __name__ == '__main__':
    print(fib5(5))
    print(fib5(50))

警告 fib5() 中 for 循环的主体使用元组拆包（tuple unpack）的方式可能有点过于讨巧。有些人可能会觉得它为了简洁而牺牲了可读性，其他一些人则可能会认为简洁本身更具可读性。要点是，last 被设置为 next 的前一个值，next 被设置为 last 的前一个值加上 next 的前一个值。这避免了创建临时变量来保存更新过程中的旧值。在 Python 中，以这种方式对某种变量交换使用元组拆包是很常见的。

使用这种方法，for 循环的主体将最多运行n - 1次。换句话说，这是迄今为止最高效版本。对于第20个元素，fib5() 需要19次调用，而 fib2() 需要21891次调用。这可能会对实际应用产生重大影响！

在递归解中，我们自顶向下工作。在这个迭代解中，我们自底向上工作。有时候递归是最直观的方法。举个例子，fib1() 和 fib2() 的核心是对原始斐波那契公式的机械转换。然而，朴素的递归解也会带来巨大的性能损失。需要记住的是，任何可以递归解决的问题也可以迭代解决。


何不试一下生成器？


到目前为止，我们已经编写了在斐波那契数列中输出单个值的函数。如果我们想要输出整个序列直到某个值呢？使用 yield 语句很容易将 fib5() 转换成 Python 生成器。当生成器被迭代时，每次迭代都会使用 yield 语句从斐波那契序列中输出一个值。

程序清单6 fib6.py

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from typing import Generator


def fib6(n: int) -> Generator[int, None, None]:
    yield 0    # special case
    if n > 0: yield 1    # special case
    last: int = 0    # initially set to fib(1)
    next: int = 1    # initially set to fib(2)
    for _ in range(1, n):
        last, next = next, last + next
        yield next


if __name__ == '__main__':
    for i in fib6(50):
        print(i)

如果你运行 fib6.py，你会看到斐波纳契数列中有51个值被打印出来。

请我喝杯咖啡吧～