姑苏城外一茅屋，万树梅花月满天

0%

pytorch | 自动求导

发表于 更新于 分类于 ， ， ， ， Valine：

构建深度学习模型的基本流程就是：搭建计算图，求得损失函数，然后计算损失函数对模型参数的导数，再利用梯度下降法等方法来更新参数。

搭建计算图的过程，称为“正向传播”，这个是需要我们自己动手的，因为我们需要设计我们模型的结构。由损失函数求导的过程，称为“反向传播”，求导是件辛苦事儿，所以自动求导基本上是各种深度学习框架的基本功能和最重要的功能之一，PyTorch也不例外。


参考资料


Tensor的自动求导
Pytorch问题：autograd与backward
pytorch的backward


设置Tensor的自动求导属性


所有的tensor都有.requires_grad属性，都可以设置成自动求导。具体方法就是在定义tensor的时候，让这个属性为True：

x = tensor.ones(2,4,requires_grad=True)
1
2
3
4
5
import torch
x = torch.ones(2,4,requires_grad=True)
print(x)
	tensor([[1., 1., 1., 1.],
       		[1., 1., 1., 1.]], requires_grad=True)

只要这样设置了之后，后面由x经过运算得到的其他tensor，就都有requires_grad=True属性了。

可以通过x.requires_grad来查看这个属性。

grad_fn 记录了这个 tensor 是经过什么操作得到的

1
2
3
4
5
6
7
8
y = x + 2
print(y)

	tensor([[3., 3., 3., 3.],
        	[3., 3., 3., 3.]], grad_fn=<AddBackward>)

y.requires_grad
True

如果想改变这个属性，就调用tensor.requires_grad_()方法：

1
2
3
4
5
6
7
x.requires_grad_(False)

	tensor([[1., 1., 1., 1.],
        	[1., 1., 1., 1.]])

print(x.requires_grad,y.requires_grad)
	False True

这里，注意区别tensor.requires_grad和tensor.requires_grad_()两个东西，前面是调用变量的属性值，后者是调用内置的函数，来改变属性。


来求导吧


下面我们来试试自动求导到底怎么样。

我们首先定义一个计算图（计算的步骤）：

1
2
3
4
x = torch.tensor([[1.,2.,3.],[4.,5.,6.]],requires_grad=True)
y = x+1
z = 2*y*y
J = torch.mean(z)

这里需要注意的是，要想使x支持求导，必须让x为浮点类型，也就是我们给初始值的时候要加个点：“.”。不然的话，就会报错。

即，不能定义[1,2,3]，而应该定义成[1.,2.,3.]，前者是整数，后者才是浮点数。

上面的计算过程可以表示为：

好了，重点注意的地方来了！

x、y、z都是tensor，但是size为（2,3）的矩阵。但是J是对z的每一个元素加起来求平均，所以J是标量。

求导，只能是【标量】对标量，或者【标量】对向量/矩阵求导！

所以，上图中，只能J对x、y、z求导，而z则不能对x求导。

我们不妨试一试：

PyTorch里面，求导是调用.backward()方法。直接调用backward()方法，会计算对计算图叶节点的导数。
获取求得的导数，用.grad方法。

试图z对x求导：

1
2
3
4
5
6
z.backward()
# 会报错：
Traceback (most recent call last)
<ipython-input-31-aa814b0a8cba> in <module>()
----> 1 z.backward()
RuntimeError: grad can be implicitly created only for scalar outputs

正确的应该是J对x求导：

1
2
3
4
5
J.backward()
x.grad

	tensor([[1.3333, 2.0000, 2.6667],
        	[3.3333, 4.0000, 4.6667]])

grad 就是导数，要求这个首先得调用 backward.

检验一下，求的是不是对的。

J对x的导数应该是什么呢？

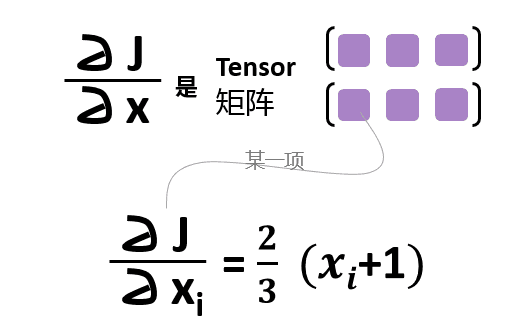
检查发现，导数就是：

[[1.3333, 2.0000, 2.6667],
[3.3333, 4.0000, 4.6667]]

总结一下，构建计算图（正向传播，Forward Propagation）和求导（反向传播，Backward Propagation）的过程就是：


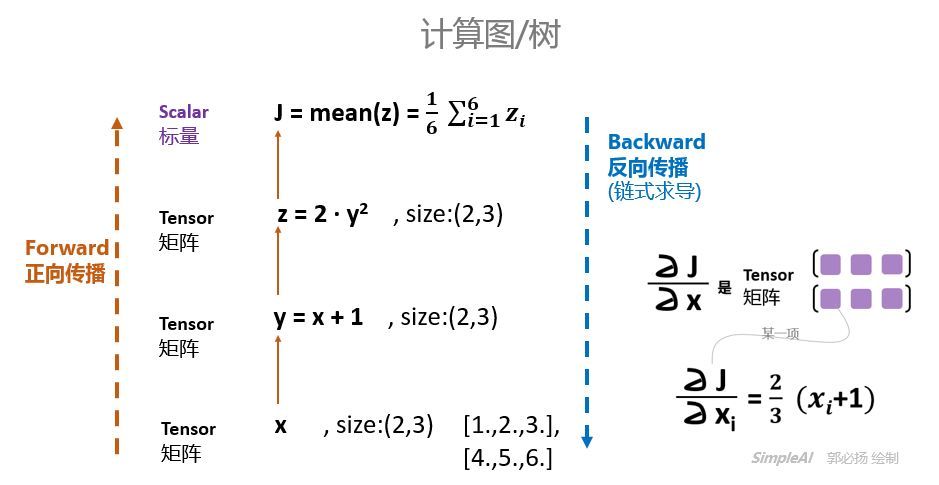
关于backward函数的一些其他问题：


在看文档的时候,他们给了这样的一个例子：

文档

1
2
3
4
5
6
7
8
9
10
11
12
x = torch.randn(3, requires_grad=True)

y = x * 2
while y.data.norm() < 1000:
    y = y * 2

v = torch.tensor([0.1, 1.0, 0.0001], dtype=torch.float)
y.backward(v)

print(x.grad)

	tensor([1.0240e+02, 1.0240e+03, 1.0240e-01])

它这里的y是一个tensor，是一个向量。按道理不能求导呀。这个参数gradients是干嘛的？

但是，如果看看backward函数的说明，会发现，里面确实有一个gradients参数：

从说明中我们可以了解到：

如果你要求导的是一个标量，那么gradients默认为None，所以前面可以直接调用J.backward()就行了

Let’s backprop now. Because out contains a single scalar, out.backward() is equivalent to out.backward(torch.tensor(1.)).

上面说，如果 backward() 是一个标量，那么其默认传的tensor 是 torch.tensor(1.)

如果你要求导的是一个张量，那么gradients应该传入一个Tensor。那么这个时候是什么意思呢？

在StackOverflow有一个解释很好：

一般来说，我是对标量求导，比如在神经网络里面，我们的loss会是一个标量，那么我们让loss对神经网络的参数w求导，直接通过loss.backward()即可。

但是，有时候我们可能会有多个输出值，比如loss=[loss1,loss2,loss3]，那么我们可以让loss的各个分量分别对x求导，这个时候就采用：

loss.backward(torch.tensor([[1.0,1.0,1.0,1.0]]))

如果你想让不同的分量有不同的权重，那么就赋予gradients不一样的值即可，比如：

loss.backward(torch.tensor([[0.1,1.0,10.0,0.001]]))

这样，我们使用起来就更加灵活了，虽然也许多数时候，我们都是直接使用.backward()就完事儿了。

我对上面的解释其实是蛮模糊的，所以，我在这边举两个例子供大家分析：

例子1

1
2
3
4
5
6
from __future__ import print_function
import torch as t
from torch.autograd import Variable
x = Variable(t.ones(2, 2),requires_grad = True)
y = x + 1
y.backward()

然后就会报上面的错误：

RuntimeError: grad can be implicitly created only for scalar outputs

因此当输出不是标量时，调用.backward()就会出错

显示声明输出的类型作为参数传入,且参数的大小必须要和输出值的大小相同

x.grad.data.zero_() #将之前的值清零
x.grad

返回：

tensor([[0., 0.],
        [0., 0.]])

进行反向传播：

y.backward(y.data)
x.grad

也可以写成，因为Variable和Tensor有近乎一致的接口

y.backward(y)
x.grad

返回：

tensor([[2., 2.],
        [2., 2.]])

但是这里返回值与预想的1不同，这个原因是得到的梯度会与参数的值相乘，所以最好传入值为1，如：

y.backward(Variable(t.ones(2, 2)))
x.grad

这样就能够成功返回想要的值了：

tensor([[1., 1.],
        [1., 1.]])

例子2

在上面的例子中，x和y都是(2,2)的数组形式，每个$ y_i $都只与对应的$ x_i $相关

如果每个yi都与多个xi相关时，梯度又是怎么计算的呢？

比如$ x = (x_1 = 2, x_2 = 4) $, $ y = ({x_1}^2 + 2x_2, 2x_1 + {3x}_2^2)$

对于 x_1 的求导：

$$ {dy_1 \over dx_1} = 2x_1 = 4 $$

$$ {dy_2 \over dx_1} = 2$$

对于 x_2 求导：

$$ {dy_1 \over dx_2} = 2 $$

$$ {dy_2 \over dx_2} = 6x_2 = 24 $$

组合

$$ {dy \over {dx}_1} = i \times {dy_1 \over dx_1} + j \times {dy_2 \over dx_1} = 4i + 2j $$


$$ {dy \over {dx}_2} = i \times {dy_1 \over dx_1} + j \times {dy_2 \over dx_1} = 2i + 24j $$

(i,j)的值就是传入.backward()的参数的值

1
2
3
4
5
6
x = Variable(t.FloatTensor([[2, 4]]),requires_grad = True)
y = Variable(t.zeros(1, 2))
y[0,0] = x[0,0]**2 + 2 * x[0,1]
y[0,1] = 2 * x[0,0] + 3 * x[0,1]**2
y.backward(Variable(t.ones(1, 2))) #（i，j）= (1,1)
x.grad

返回：

tensor([[ 6., 26.]])

例子3

如果x和y不是相同的数组形式，且每个$ y_i $都与多个$ x_i $相关时，梯度又是怎么计算的呢？

比如$ x = (x_1 = 2, x_2 = 4, x_3=5) $,$ y = ({x}_1^2 + 2x_2 + 4x_3,2x_1+{3x}_2^2+x_3^2) $

1
2
3
4
5
6
x = Variable(t.FloatTensor([[2, 4, 5]]),requires_grad = True)
y = Variable(t.zeros(1, 2))
y[0,0] = x[0,0]**2 + 2 * x[0,1] + 4 * x[0,2]
y[0,1] = 2 * x[0,0] + 3 * x[0,1]**2 + x[0,2]**2
y.backward(Variable(t.ones(1, 2)))
x.grad

返回：

tensor([[ 6., 26., 14.]])

如果(i, j) = (2,2),结果是否为(12, 52, 28)呢？

1
2
3
4
5
6
x = Variable(t.FloatTensor([[2, 4, 5]]),requires_grad = True)
y = Variable(t.zeros(1, 2))
y[0,0] = x[0,0]**2 + 2 * x[0,1] + 4 * x[0,2]
y[0,1] = 2 * x[0,0] + 3 * x[0,1]**2 + x[0,2]**2
y.backward(Variable(t.FloatTensor([[2, 2]])))
x.grad

返回：

tensor([[12., 52., 28.]])

上面的验证自己在草纸上进行演算，在这里不给出。

例子4

如果你想要分别得到$ y_1,y_2 $对$ x_1,x_2,x_3 $的求导值，方法是：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
x = Variable(t.FloatTensor([[2, 4, 5]]),requires_grad = True)
y = Variable(t.zeros(1, 2))
y[0,0] = x[0,0]**2 + 2 * x[0,1] + 4 * x[0,2]
y[0,1] = 2 * x[0,0] + 3 * x[0,1]**2 + x[0,2]**2
j = t.zeros(3,2)#用于存放求导的值
#(i,j)=(1,0)这样就会对应只求得y1对x1,x2和x3的求导
#retain_variables=True的作用是不在反向传播后释放内存，这样才能够再次反向传播
y.backward(Variable(t.FloatTensor([[1, 0]])),retain_variables=True) 
j[:,0] = x.grad.data
x.grad.data.zero_() #将之前的值清零
#(i,j)=(1,0)这样就会对应只求得y2对x1,x2和x3的求导
y.backward(Variable(t.FloatTensor([[0, 1]]))) 
j[:,1] = x.grad.data
print(j)

报错：

TypeError: backward() got an unexpected keyword argument 'retain_variables'

原因是新版本使用的参数名为retain_graph，改了即可：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
x = Variable(t.FloatTensor([[2, 4, 5]]),requires_grad = True)
y = Variable(t.zeros(1, 2))
y[0,0] = x[0,0]**2 + 2 * x[0,1] + 4 * x[0,2]
y[0,1] = 2 * x[0,0] + 3 * x[0,1]**2 + x[0,2]**2
j = t.zeros(3,2)#用于存放求导的值
#(i,j)=(1,0)这样就会对应只求得y1对x1,x2和x3的求导
#retain_graph=True的作用是不在反向传播后释放内存，这样才能够再次反向传播
y.backward(Variable(t.FloatTensor([[1, 0]])),retain_graph=True) 
j[:,0] = x.grad.data
x.grad.data.zero_() #将之前的值清零
#(i,j)=(1,0)这样就会对应只求得y2对x1,x2和x3的求导
y.backward(Variable(t.FloatTensor([[0, 1]]))) 
j[:,1] = x.grad.data
print(j)

返回：

tensor([[ 4.,  2.],
        [ 2., 24.],
        [ 4., 10.]])

一个计算图只能backward一次

一个计算图在进行反向求导之后，为了节省内存，这个计算图就销毁了。

如果你想再次求导，就会报错。

比如你定义了计算图：

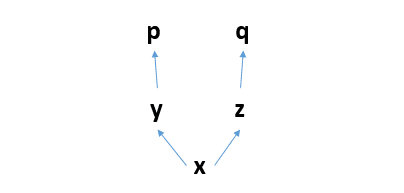
你先求p求导，那么这个过程就是反向的p对y求导，y对x求导。

求导完毕之后，这三个节点构成的计算子图就会被释放：

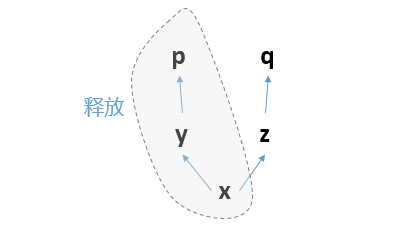
那么计算图就只剩下z、q了，已经不完整，无法求导了。

所以这个时候，无论你是想再次运行p.backward()还是q.backward()，都无法进行，报错如下：

RuntimeError: Trying to backward through the graph a second time, but the buffers have already been freed. Specify retain_graph=True when calling backward the first time.

好，怎么办呢？

遇到这种问题，一般两种情况：

1

你的实际计算，确实需要保留计算图，不让子图释放

那么，就更改你的backward函数，添加参数retain_graph=True，重新进行backward，这个时候你的计算图就被保留了，不会报错。

但是这样会吃内存！，尤其是，你在大量迭代进行参数更新的时候，很快就会内存不足，memory out了。

2

你实际根本没必要对一个计算图backward多次，而你不小心多跑了一次backward函数

通常，你要是在IPython里面联系PyTorch的时候，因为你会反复运行一个单元格的代码，所以很容易一不小心把backward运行了多次，就会报错。这个时候，你就检查一下代码，防止backward运行多次即可。

请我喝杯咖啡吧～