这是一个简单的实现,关于 GAN 的例子。
参考资料
论文
想要学习 GAN 最开始的论文当然要看一下。
原理
GAN 的原理很简单,就是一个博弈过程。举一个简单的例子,有一个警察,他有认识假币的先验经验「GAN 的判别器一开始也是没有先验经验的,刚开始也是要学习一下的」。有一个罪犯,他想制作假币。由于,初期,罪犯的制造假币的技术不高,所以,警察很容易就查看出哪些是假币。罪犯,得到假币漏洞的反馈后,提升自己的假币技术。而,警察看到假币的技术提升,也在提升自己的鉴别能力。这样,两者相互博弈,罪犯的假币技术越来越厉害,警察的鉴别技术也越来越厉害。
在原文中有这样的图
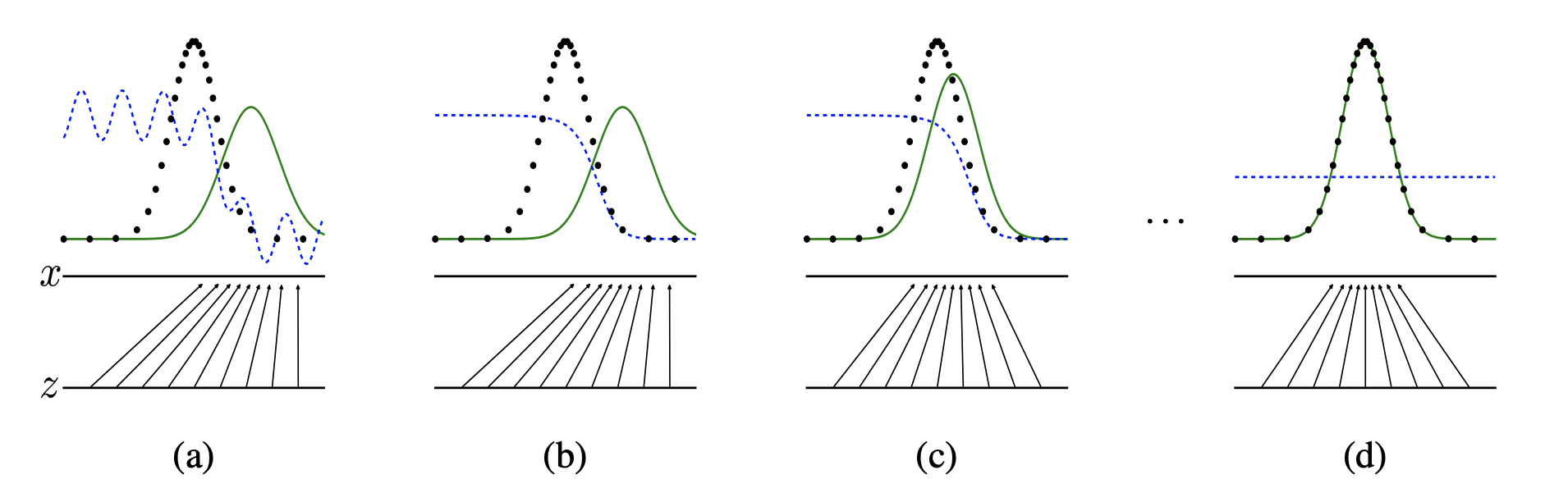
说实话,这个图我理解不了。「主要是理解不了蓝色的部分」
- 黑色点线为训练集数据分布曲线
- 蓝色点线为判别器输出的分布曲线
- 绿色实线为生成器输出的分布曲线
- z展示的是生成器映射前的简单概率分布(一般是高斯分布)的范围和密度
- x展示的是生成器映射后学到的训练集的概率分布的范围和密度
这张图就是生成器通过不断的学习,让自己的分布变成真实数据的分布。
- (a)判别器与生成器均未训练呈随机分布
- (b)判别器经过训练,输出的分布在靠近训练集“真”数据分布的区间趋近于1(真),在靠近生成器生成的“假”数据分布的区间趋近于0(假)
- (c)生成器根据判别器输出的(真假)分布,更新参数,使自己的输出分布趋近于训练集“真”数据的分布。
经过(b)(c)(b)(c)…步骤的循环交替。判别器的输出分布随着生成器输出的分布与训练集分布的接近而更加平缓;生成器输出的分布则在判别器输出分布的指引下逐渐趋近于训练集“真”数据的分布。
- (d)训练完成时,生成器输出的分布完美拟合了训练集数据的分布,判别器的输出由于生成器的完美拟合而无法判别生成器输出的真伪而呈一条取值约为0.5(真假之间)的直线。
对于,警察来说,其为判别模型,也就是一个二分类器,用来判断样本输入的真假。
对于,罪犯来说,这是一个样本生成器,用来生成一个逼真的样本。
在这里我们只针对最初始的论文来说,并不说各种变种。
公式
$$ \mathop{min}\limits_{G}\mathop{max}\limits_{D}V(D,G) = \mathbb{E}{x \sim p_{data(x)}}\left[\log D(x)\right] + \mathbb{E}{z \sim p(z)}\left[\log \left(1-D(G(z))\right)\right] $$
- x 是真实图像
- z 是噪声「根据噪声来生成图像」
上面是两个公式和在一起,其实可以拆成两个。
判别器
$$ \mathop{max}\limits_{D}V(D,G) = \mathbb{E}{x \sim p_{data(x)}}\left[\log D(x)\right] + \mathbb{E}{z \sim p(z)}\left[\log \left(1-D(G(z))\right)\right] $$
所以,对于生成器而言。
我希望,我能正确的区分哪个是真的,哪个是假的,所以,生成器希望 D(x) 为 1 判断真的为真, D(G(z)) 为 0 判断假的为假。
当 D(x) 趋向于 1 的时候,D(G(z)) 趋向于 0 的时候。对于,判别器而言是取最大值。
因为,当 D(x) 错分为 0 的时候 logD(x) 会变成负无穷。当 D(G(z)) 被错分为 1 的时候,log(1-D(G(z))) 也会变成负无穷大。
生成器
$$ \mathop{min}\limits_{G}V(D,G) = \mathbb{E}{z \sim p(z)}\left[\log \left(1-D(G(z))\right)\right] $$
对于生成器而言,我希望 D(G(z)) 总是为 1,所以,根据上面的理论,我希望值越来越小。
看了之后是不是很懵逼,其实,这是用数学的语言来描述的,理解起来总是有点抽象,我更建议看代码,你可以直接看下面的代码。
训练
在最原始的论文中,使用的是最简单的 DNN 网络,这里我们不讨论什么网络结构,而是讨论相关的训练过程。
训练判别器
在训练的一开始,生成器和判别器,都是随机的,这个时候,我们固定生成器,先训练判别器,这样,我们的判别器就有了先验经验,可以区分什么是真什么是假。
训练生成器
在有了判别器的先验经验后,我们固定判别器,然后训练生成器。
重复上面的步骤。
其实,说到这里,很多人还是懵逼,所以,我建议直接看代码。