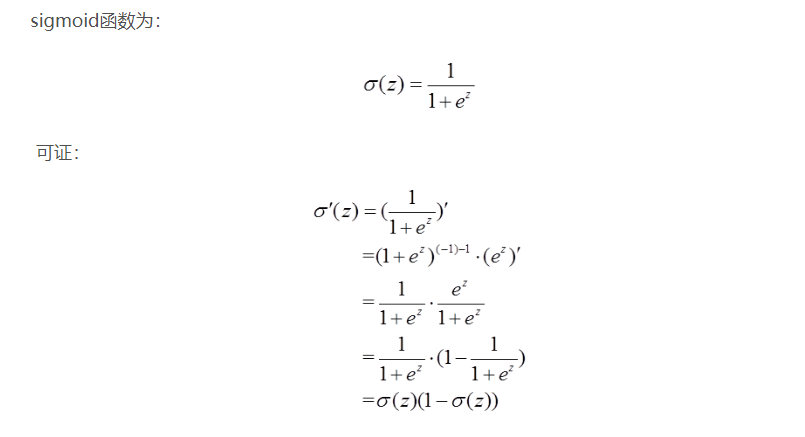如题,这是深度学习的内容,希望各位看官喜欢。
额,本来这是写在 signal 类别中的,但是后来发现这个和深度学习更加相关,但是最后把它归到机器学习的类别。
但是,图片资源放在 signal 中,希望后来修改的时候,可以注意这一点。
参考资料
如何通俗的解释交叉熵与相对熵? - Noriko Oshima的回答 - 知乎
信息论
交叉熵是信息论中的一个概念,要想了解交叉熵的本质,需要先从最基本的概念讲起。
信息量
首先是信息量。假设我们听到了两件事,分别如下:
事件A:巴西队进入了2018世界杯决赛圈。
事件B:中国队进入了2018世界杯决赛圈。 仅凭直觉来说,显而易见事件B的信息量比事件A的信息量要大。究其原因,是因为事件A发生的概率很大,事件B发生的概率很小。所以当越不可能的事件发生了,我们获取到的信息量就越大。越可能发生的事件发生了,我们获取到的信息量就越小。那么信息量应该和事件发生的概率有关。
假设$ X $ 是一个离散型随机变量,其取值集合为 $ \chi $ ,概率分布函数 $ p(x)=Pr(X=x),x\in\chi $,则定义事件$ X=x_0 $ 的信息量为:
$$ I(x_0)=-log(p(x_0)) $$
由于是概率所以 $ p(x_0) $ 的取值范围是 $ [0,1] $,绘制为图形如下:

可见该函数符合我们对信息量的直觉
熵
熵的本质是香农信息量 $ log {1 \over p }$ 的期望。
考虑另一个问题,对于某个事件,有$ n $种可能性,每一种可能性都有一个概率$ p(x_i) $
这样就可以计算出某一种可能性的信息量。举一个例子,假设你拿出了你的电脑,按下开关,会有三种可能性,下表列出了每一种可能的概率及其对应的信息量
序号 事件 概率p 信息量I
A 电脑正常开机 0.7 -log(p(A))=0.36
B 电脑无法开机 0.2 -log(p(B))=1.61
C 电脑爆炸了 0.1 -log(p(C))=2.30我们现在有了信息量的定义,而熵用来表示所有信息量的期望,即:
$$ H(X)=-\sum_{i=1}^n p(x_i)log(p(x_i)) $$
其中$ n $代表所有的$ n $种可能性,所以上面的问题结果就是
$$ H(X)=-[p(A)log(p(A))+p(B)log(p(B))+p(C))log(p(C))] $$
$$ = 0.7\times 0.36+0.2\times 1.61+0.1\times 2.30 =0.804 $$
然而有一类比较特殊的问题,比如投掷硬币只有两种可能,字朝上或花朝上。买彩票只有两种可能,中奖或不中奖。我们称之为0-1分布问题(二项分布的特例),对于这类问题,熵的计算方法可以简化为如下算式:
$$ H(X)=-\sum_{i=1}^n p(x_i)log(p(x_i)) $$
$$ =-p(x)log(p(x))-(1-p(x))log(1-p(x)) $$
相对熵(KL散度)
知乎上的解释
现有关于样本集的2个概率分布 $ p $和$ q $,其中$ p $为真实分布,$ q $非真实分布。按照真实分布$ p $来衡量识别一个样本的所需要的编码长度的期望(即平均编码长度)为:
$$ H(p) = \sum_i p(i) \times log {1 \over p(i)} $$
如果使用错误分布 $ q $ 来表示来自真实分布 $ p $ 的平均编码长度,则应该是:
$$ H(p,q)= \sum_i p(i) \times log {1 \over q(i)} $$
因为用 $ q $ 来编码的样本来自分布 $ p $ ,所以期望 $ H(p,q) $ 中概率是 $ p(i) $ 。$ H(p,q) $ 我们称之为“交叉熵”。
比如含有 $ 4 $ 个字母 $ (A,B,C,D) $ 的数据集中,真实分布 $ p=({1 \over 2}, {1 \over 2}, 0, 0) $ ,即$ A $ 和 $ B $ 出现的概率均为 $ 1 \over 2 $,$ C $ 和 $ D $ 出现的概率都为 $ 0 $ 。计算 $ H(p) $ 为 $ 1 $ ,即只需要 $ 1 $ 位编码即可识别 $ A $ 和 $ B $ 。如果使用分布 $ Q=({1 \over 4},{ 1 \over 4},{ 1 \over 4 },{ 1 \over 4}) $来编码则得到 $ H(p,q)=2 $ ,即需要 $ 2 $ 位编码来识别 $ A $ 和 $ B $ (当然还有 $ C $ 和 $ D $ ,尽管 $ C $ 和 $ D $ 并不会出现,因为真实分布 $ p $ 中 $ C $ 和 $ D $ 出现的概率为 $ 0 $ ,这里就钦定概率为 $ 0 $ 的事件不会发生啦)。
可以看到上例中根据非真实分布 $ q $ 得到的平均编码长度 $ H(p,q) $ 大于根据真实分布 $ p $ 得到的平均编码长度 $ H(p) $ 。事实上,根据Gibbs’ inequality可知, $ H(p,q)>=H(p) $ 恒成立,当 $ q $ 为真实分布 $ p $ 时取等号。我们将由 $ q $ 得到的平均编码长度比由 $ p $ 得到的平均编码长度多出的bit数称为“相对熵”:
$$ D(p||q) = H(p,q) - H(p) = \sum_i p(i) \times log ({p(i) \over {q(i)}}) $$
其又被称为KL散度 Kullback–Leibler divergence,KLD
它表示 $ 2 $个函数或概率分布的差异性:差异越大则相对熵越大,差异越小则相对熵越小,特别地,若 $ 2 $ 者相同则熵为 $ 0 $ 。注意,KL散度的非对称性。
比如TD-IDF算法就可以理解为相对熵的应用:词频在整个语料库的分布与词频在具体文档中分布之间的差异性。
交叉熵可在神经网络(机器学习)中作为损失函数, $ p $ 表示真实标记的分布, $ q $ 则为训练后的模型的预测标记分布,交叉熵损失函数可以衡量 $ p $ 与 $ q $ 的相似性。交叉熵作为损失函数还有一个好处是使用 sigmoid 函数在梯度下降时能避免均方误差损失函数学习速率降低的问题,因为学习速率可以被输出的误差所控制。
对上面的话做解释
从方差代价函数说起
代价函数经常用方差代价函数(即采用均方误差MSE),比如对于一个神经元(单输入单输出,sigmoid函数),定义其代价函数为:
$$ C = \frac{(y-a)^2}{2} $$
其中y是我们期望的输出,a为神经元的实际输出.
$ a = \sigma(z) $ , $ z = wz + b $
在训练神经网络过程中,我们通过梯度下降算法来更新w和b,因此需要计算代价函数对w和b的导数:
$$ \frac{\alpha C}{\alpha w} = (a - y) \sigma^{’} (z)x = a \sigma^{’} (z) $$
$$ \frac{\alpha C}{\alpha b} = (a - y) \sigma^{’} (z) = a \sigma^{’} (z) $$
然后更新w、b:
$$ w = w - \eta \times \frac{\alpha C}{\alpha w} = w - \eta \times a \times \sigma^{’} {(z)}$$
$$ b = b - \eta \times \frac{\alpha C}{\alpha b} = w - \eta \times a \times \sigma^{’} {(z)}$$
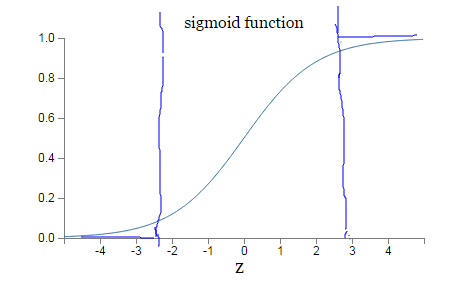
因为sigmoid函数的性质,导致 $ σ′(z) $ 在 $ z $ 取大部分值时会很小(如下图标出来的两端,几近于平坦),这样会使得 $ w $ 和 $ b $ 更新非常慢(因为 ηaσ′(z) 这一项接近于0)。
交叉熵代价函数(cross-entropy cost function)
为了克服这个缺点,引入了交叉熵代价函数(下面的公式对应一个神经元,多输入单输出):
$$ C = -\frac{1}{n} \sum_x [ylna + (1-y)ln(1-a)]$$
其中y为期望的输出,a为神经元实际输出
$a = σ(z) $,$ z = \sum w_j \times x_j + b $
与方差代价函数一样,交叉熵代价函数同样有两个性质:
非负性。(所以我们的目标就是最小化代价函数)
当真实输出a与期望输出y接近的时候,代价函数接近于0.(比如 y=0 ,a~0 ;y=1 , a~1 时,代价函数都接近0)。另外,它可以克服方差代价函数更新权重过慢的问题。我们同样看看它的导数:
$$ \frac{\alpha C}{\alpha w_j} = \frac{1}{n} \sum_x x_j (\sigma(z) - y)$$
$$ \frac{\alpha C}{\alpha b} = \frac{1}{n} \sum_x x_j (\sigma(z) - y)$$
可以看到,导数中没有 $σ′(z)$ 这一项,权重的更新是受 $σ(z)−y$ 这一项影响,即受误差的影响。所以当误差大的时候,权重更新就快,当误差小的时候,权重的更新就慢。这是一个很好的性质。
总结
当我们用sigmoid函数作为神经元的激活函数时,最好使用交叉熵代价函数来替代方差代价函数,以避免训练过程太慢。
不过,你也许会问,为什么是交叉熵函数?导数中不带 $ σ′(z) $ 项的函数有无数种,怎么就想到用交叉熵函数?这自然是有来头的,更深入的讨论就不写了,少年请自行了解。
另外,交叉熵函数的形式是 $−[ylna+(1−y)ln(1−a)] $而不是 $−[alny+(1−a)ln(1−y)]$ ,为什么?因为当期望输出的 $y=0$ 时,$lny$ 没有意义;当期望 $y=1$ 时,$ln(1-y)$ 没有意义。而因为 $a$ 是sigmoid函数的实际输出,永远不会等于0或1,只会无限接近于0或者1,因此不存在这个问题。
还要说说:log-likelihood cost
对数似然函数也常用来作为softmax回归的代价函数,在上面的讨论中,我们最后一层(也就是输出)是通过sigmoid函数,因此采用了交叉熵代价函数。而深度学习中更普遍的做法是将softmax作为最后一层,此时常用的是代价函数是log-likelihood cost。
In fact, it’s useful to think of a softmax output layer with log-likelihood cost as being quite similar to a sigmoid output layer with cross-entropy cost。
其实这两者是一致的,logistic回归用的就是sigmoid函数,softmax回归是logistic回归的多类别推广。log-likelihood代价函数在二类别时就可以化简为交叉熵代价函数的形式。
另外一个解释
相对熵又称$ KL $散度,如果我们对于同一个随机变量$ x $有两个单独的概率分布 $ P(x) $ 和 $ Q(x) $,我们可以使用$ KL $散度(Kullback-Leibler (KL) divergence)来衡量这两个分布的差异
维基百科对相对熵的定义
In the context of machine learning, DKL(P‖Q) is often called the information gain achieved if P is used instead of Q.
即如果用$ P $来描述目标问题,而不是用$ Q $来描述目标问题,得到的信息增量。
在机器学习中,$ P $往往用来表示样本的真实分布,比如$ [1,0,0] $表示当前样本属于第一类。$ Q $用来表示模型所预测的分布,比如$ [0.7,0.2,0.1] $
直观的理解就是如果用$ P $来描述样本,那么就非常完美。而用$ Q $来描述样本,虽然可以大致描述,但是不是那么的完美,信息量不足,需要额外的一些“信息增量”才能达到和$ P $一样完美的描述。如果我们的$ Q $通过反复训练,也能完美的描述样本,那么就不再需要额外的“信息增量”,$ Q $等价于$ P $。
KL散度的计算公式:
$$ D_{KL}(p||q)=\sum_{i=1}^np(x_i)log(\frac{p(x_i)}{q(x_i)}) \tag{3.1} $$
$ n $为事件的所有可能性。
$ D_{KL} $的值越小,表示$ q $分布和$ p $分布越接近
交叉熵
对式3.1变形可以得到:
$$ D_{KL}(p||q) = \sum_{i=1}^np(x_i)log(p(x_i))-\sum_{i=1}^np(x_i)log(q(x_i)) $$
$$ = -H(p(x))+[-\sum_{i=1}^np(x_i)log(q(x_i))] $$
等式的前一部分恰巧就是p的熵,等式的后一部分,就是交叉熵:
$$ H(p,q)=-\sum_{i=1}^np(x_i)log(q(x_i)) $$
在机器学习中,我们需要评估label和predicts之间的差距,使用KL散度刚刚好,即 $ D_{KL}(y||\hat{y}) $,由于KL散度中的前一部分 $ −H(y) $ 不变,故在优化过程中,只需要关注交叉熵就可以了。所以一般在机器学习中直接用用交叉熵做loss,评估模型。
机器学习中交叉熵的应用
为什么要用交叉熵做loss函数?
在线性回归问题中,常常使用MSE(Mean Squared Error)作为loss函数,比如:
$$ loss = \frac{1}{2m}\sum_{i=1}^m(y_i-\hat{y_i})^2 $$
这里的m表示m个样本的,loss为m个样本的loss均值。
MSE在线性回归问题中比较好用,那么在逻辑分类问题中还是如此么?
交叉熵在单分类问题中的使用
这里的单类别是指,每一张图像样本只能有一个类别,比如只能是狗或只能是猫。
交叉熵在单分类问题上基本是标配的方法
$$ loss=-\sum_{i=1}^{n}y_ilog(\hat{y_i}) \tag{2.1} $$
上式为一张样本的loss计算方法。式2.1中n代表着n种类别。
举例说明,比如有如下样本

对应的标签和预测值
* 猫 青蛙 老鼠
Label 0 1 0
Pred 0.3 0.6 0.1那么
$$ loss=-(0\times log(0.3)+1\times log(0.6)+0\times log(0.1) $$
$$ =-log(0.6) $$
对应一个batch的loss就是
$$ loss=-\frac{1}{m}\sum_{j=1}^m\sum_{i=1}^{n}y_{ji}log(\hat{y_{ji}}) $$
m为当前batch的样本数
交叉熵在多分类问题中的使用
这里的多类别是指,每一张图像样本可以有多个类别,比如同时包含一只猫和一只狗
和单分类问题的标签不同,多分类的标签是n-hot。
比如下面这张样本图,即有青蛙,又有老鼠,所以是一个多分类问题

对应的标签和预测值
* 猫 青蛙 老鼠
Label 0 1 1
Pred 0.1 0.7 0.8值得注意的是,这里的Pred不再是通过softmax计算的了,这里采用的是sigmoid。将每一个节点的输出归一化到[0,1]之间。所有Pred值的和也不再为1。换句话说,就是每一个Label都是独立分布的,相互之间没有影响。所以交叉熵在这里是单独对每一个节点进行计算,每一个节点只有两种可能值,所以是一个二项分布。前面说过对于二项分布这种特殊的分布,熵的计算可以进行简化。
同样的,交叉熵的计算也可以简化,即
$$ loss =-ylog(\hat{y})-(1-y)log(1-\hat{y}) $$
注意,上式只是针对一个节点的计算公式。这一点一定要和单分类loss区分开来。
例子中可以计算为:
$$loss_猫 =-0\times log(0.1)-(1-0)log(1-0.1)=-log(0.9)$$
$$loss_蛙 =-1\times log(0.7)-(1-1)log(1-0.7)=-log(0.7)$$
$$loss_鼠 =-1\times log(0.8)-(1-1)log(1-0.8)=-log(0.8)$$
单张样本的loss即为 $loss = loss_猫+loss_蛙+loss_鼠$
每一个batch的loss就是:
$$loss =\sum_{j=1}^{m}\sum_{i=1}^{n}-y_{ji}log(\hat{y_{ji}})-(1-y_{ji})log(1-\hat{y_{ji}})$$
式中m为当前batch中的样本量,n为类别数。
题外话
交叉熵代价函数(Cross-entropy cost function)是用来衡量人工神经网络(ANN)的预测值与实际值的一种方式。与二次代价函数相比,它能更有效地促进ANN的训练。在介绍交叉熵代价函数之前,本文先简要介绍二次代价函数,以及其存在的不足。
二次代价函数的不足
ANN的设计目的之一是为了使机器可以像人一样学习知识。人在学习分析新事物时,当发现自己犯的错误越大时,改正的力度就越大。比如投篮:当运动员发现自己的投篮方向离正确方向越远,那么他调整的投篮角度就应该越大,篮球就更容易投进篮筐。同理,我们希望:ANN在训练时,如果预测值与实际值的误差越大,那么在反向传播训练的过程中,各种参数调整的幅度就要更大,从而使训练更快收敛。然而,如果使用二次代价函数训练ANN,看到的实际效果是,如果误差越大,参数调整的幅度可能更小,训练更缓慢。
以一个神经元的二类分类训练为例,进行两次实验(ANN常用的激活函数为sigmoid函数,该实验也采用该函数):输入一个相同的样本数据x=1.0(该样本对应的实际分类y=0);两次实验各自随机初始化参数,从而在各自的第一次前向传播后得到不同的输出值,形成不同的代价(误差):
实验1:第一次输出值为0.82
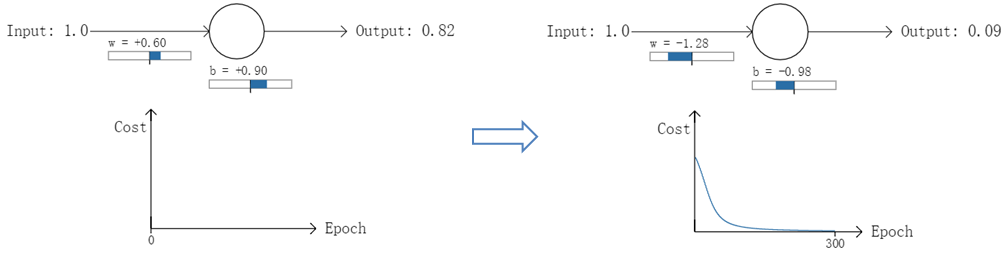
实验2:第一次输出值为0.98

在实验1中,随机初始化参数,使得第一次输出值为0.82(该样本对应的实际值为0);经过300次迭代训练后,输出值由0.82降到0.09,逼近实际值。而在实验2中,第一次输出值为0.98,同样经过300迭代训练,输出值只降到了0.20。
从两次实验的代价曲线中可以看出:实验1的代价随着训练次数增加而快速降低,但实验2的代价在一开始下降得非常缓慢;直观上看,初始的误差越大,收敛得越缓慢。
其实,误差大导致训练缓慢的原因在于使用了二次代价函数。二次代价函数的公式如下:
$$C = \frac{1}{2n} \sum_x ||y(x) - a^{L}(x)||^2$$
其中,C表示代价,x表示样本,y表示实际值,a表示输出值,n表示样本的总数。为简单起见,同样一个样本为例进行说明,此时二次代价函数为:
$$ C = \frac{(y-a)^2}{2}$$
目前训练ANN最有效的算法是反向传播算法。简而言之,训练ANN就是通过反向传播代价,以减少代价为导向,调整参数。参数主要有:神经元之间的连接权重w,以及每个神经元本身的偏置b。调参的方式是采用梯度下降算法(Gradient descent),沿着梯度方向调整参数大小。w和b的梯度推导如下:
$$\frac{\alpha C}{\alpha w} = (a-y)\sigma^{’}(z)x$$
$$\frac{\alpha C}{\alpha w} = (a-y)\sigma^{’}(z)$$
其中,z表示神经元的输入,表示激活函数。从以上公式可以看出,w和b的梯度跟激活函数的梯度成正比,激活函数的梯度越大,w和b的大小调整得越快,训练收敛得就越快。而神经网络常用的激活函数为sigmoid函数,该函数的曲线如下所示:
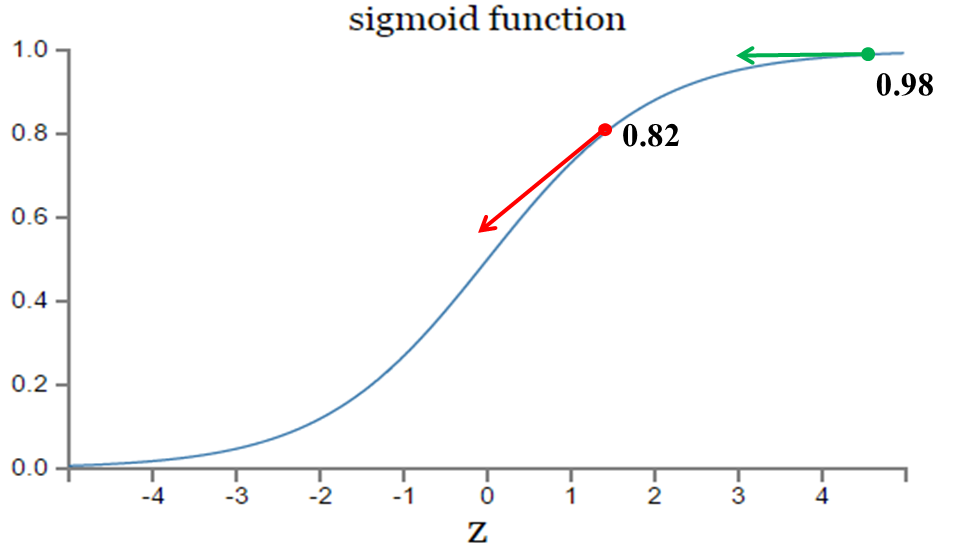
如图所示,实验2的初始输出值(0.98)对应的梯度明显小于实验1的输出值(0.82),因此实验2的参数梯度下降得比实验1慢。这就是初始的代价(误差)越大,导致训练越慢的原因。与我们的期望不符,即:不能像人一样,错误越大,改正的幅度越大,从而学习得越快。
可能有人会说,那就选择一个梯度不变化或变化不明显的激活函数不就解决问题了吗?图样图森破,那样虽然简单粗暴地解决了这个问题,但可能会引起其他更多更麻烦的问题。而且,类似sigmoid这样的函数(比如tanh函数)有很多优点,非常适合用来做激活函数,具体请自行google之。
交叉熵代价函数
换个思路,我们不换激活函数,而是换掉二次代价函数,改用交叉熵代价函数:
$$C = -\frac{1}{n} \sum_x [ylna + (1-y)ln(1-a)]$$
其中,x表示样本,n表示样本的总数。那么,重新计算参数w的梯度:

其中(具体证明见附录):
$$ \sigma^{’}(z) = \sigma (z)(1-\sigma(z))$$
因此,w的梯度公式中原来的 $\sigma^{’}(z)$ 被消掉了;另外,该梯度公式中的 $\sigma(z)-y$ 表示输出值与实际值之间的误差。所以,当误差越大,梯度就越大,参数w调整得越快,训练速度也就越快。同理可得,b的梯度为:
$$\frac{\alpha C}{\alpha b} = \frac{1}{n} \sum_x (\sigma(z) - y)$$
实际情况证明,交叉熵代价函数带来的训练效果往往比二次代价函数要好。
交叉熵代价函数是如何产生的?
以偏置b的梯度计算为例,推导出交叉熵代价函数:
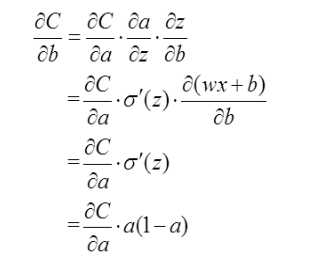
在上面,由二次代价函数推导出来的b的梯度公式为:
$$\frac{\alpha C}{\alpha b} = (a - y)\sigma^{’}(z)$$
为了消掉该公式中的 $\sigma^{’}(z)$,我们想找到一个代价函数使得:
$$\frac{\alpha C}{\alpha b}=(a-y)$$
即
$$\frac{\alpha C}{\alpha a} * a(1-a)=(a-y)$$
对两侧求积分,可得:
$$C = -[ylna + (1-y)ln(1-a)] + constant $$
而这就是前面介绍的交叉熵代价函数。
附录