这一章中我们可以学到什么是连乘,总和,连锁规则。
很有趣。。。
总和规则
比如这个函数的导数应该怎么理解
f(x^2 + sin(θ))看如下的图例:
首先我们知道 f(x^2 + sin(θ)) 的高度就是 x^2 和 sin(θ) 的高度和。
那么 d(x^2 + sin(θ)) 就是这个函数高度的增量。
那相应的增量也就是分函数 x^2 的增量和 sin(θ) 的增量和。
则 d(x^2) = 2xdx ,d(sin(θ)) = cos(θ)dx
所以,最后 d(x^2 + sin(θ)) = 2xdx + cos(θ)dx
连乘规则
比如下面这个函数的导数如何理解
f(x^2 * sin(θ))看如下的图例:
其实,这个就可以解读为边为 sin(θ) 和 边为 x^2 的矩形面积。
所以,对于一条边的增量是 d(sin(θ)) ,对于另一条边的增量就是 d(x^2)
根据以前的理论,我们可以得知一共会多出三块面积,但是占据主面积的只有两块。
即: d(sin(θ)) * x^2 和 sin(θ) * d(x^2)
所以
d(f(x^2 * sin(θ))) = d(sin(θ)) * x^2 + sin(θ) * d(x^2)
= cos(θ) * x^2 *dx + sin(θ) * 2xdx连锁规则
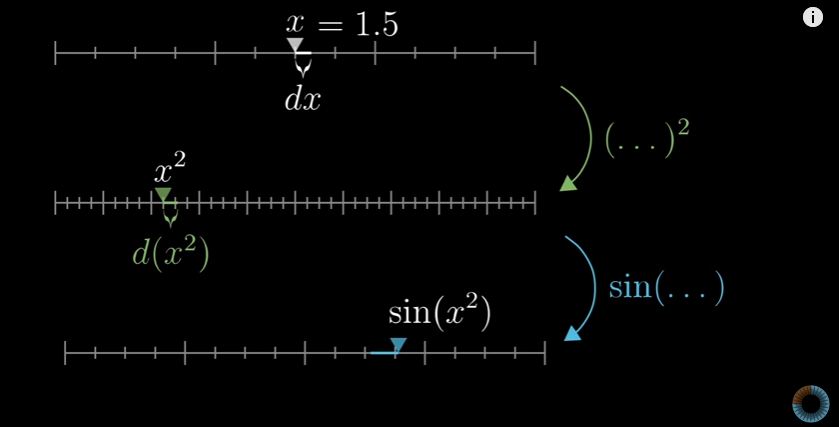
比如这个函数的导数应该怎么理解
f(x) = sin(x^2)看如下的图例:
x 变化,最先变化的是 x^2 ,然后才是 sin
当 x 增量的时候,第二段的增量是 d(x^2),我们将 x^2 看做 h
那么第三段的增量就是 d(sin(h)) = cos(h)dh
将 x^2 带入 h 中,上面的式子就变成了
cos(x^2)d(x^2) = 2xcos(x^2)dx