这一章涉及了导数的本质,是十分重要的一章。
学过微分的都知道下面的式子:
d(x^2)/d(x) = 2x那么这个导数的几何意义是什么?
在上一章我们有这样一个结论:
导数从本质上讲只是关注着某一个量(dx)的微小变化,以及与之关联的另一个量(dy)的微小变化。我们的目标函数是 x^2 ,想象成几何的话,就是正方形的面积。因为是一个微小的变化量,所谓的导数就是让正方形的边稍微增加一点微小的长度 dx ,而导数就是增加的面积。
我们可以从上面的那个图得知,其实增加的面积是三块,即
df = 2xdx + (dx)^2
但是由于 dx 是一个非常小的数,所以,后面那个是可以忽略的,最后就变成
df = 2xdx
变化形式
df/dx = 2x现在我们再考虑一下 f(x) = x^3
其边增加一个微小的变量 dx ,所以,其实增加的体积是 7 块,其中 3 块是 3x^2dx ,另外三块是 3dx^2 另外一块是 dx^3
我们根据上面的运算可以得知,后面那两项是可以忽略的。
所以最后我们的体积变化率可以看成
df = 3*x^2dx
变换后
df/dx = 3x^2现在我们换一个更加复杂的式子
x^n
其相当于每个边都增加了 dx,即下面
(x + dx)^n经过拆项我们可以拆出三个主体,第一个主体是 x^n 这个相当于原来的体积,具体一点相当于上面例子中正方形原本的面积和正方体原本的体积。而图片中第二项就是增加的体积中占比很大的主体,由于第三项中都是 (dx)^2 的式子,所以都可以忽略。
到了此时,我们就很容易的可以得出,其导数的形式是:
df/dx = n(x^n-1)以上便是以微小增量的角度看导数。
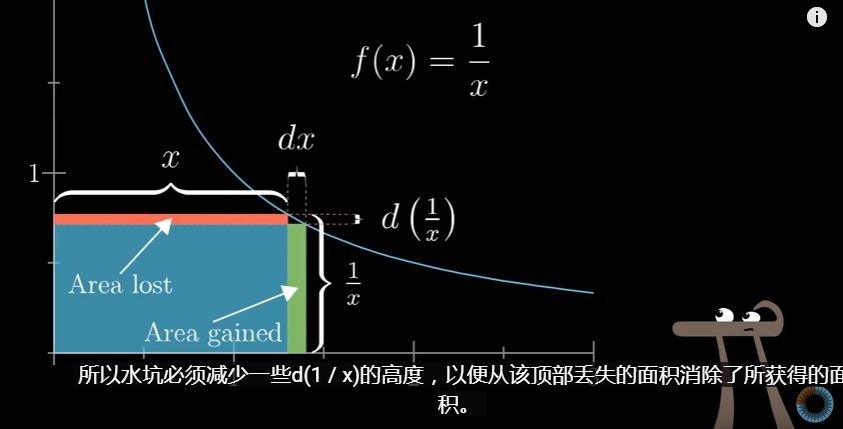
我们来看一个更有意思的函数。。。f(x) = 1/x
首先我们知道这个函数代表面积永远是 1,即 x * 1/x = 1
当在横坐标延长 dx 的时候,相应的高度就会减小 -d(1/x)
即 dx 的变化假设是从 x1 - x2
那么 dx = d(x2 - x1)
而高度的变化就是 1/x1 - 1/x2
即 d(1/x) = -d(1/x1 - 1/x2)因为我们的面积是恒定的,所以增加的就相当于是减少的,即
dx * 1/x = -d(1/x) * x
变换可以得出
d(1/x)/d(x) = -1/(x^2)以上便是它的几何意义。
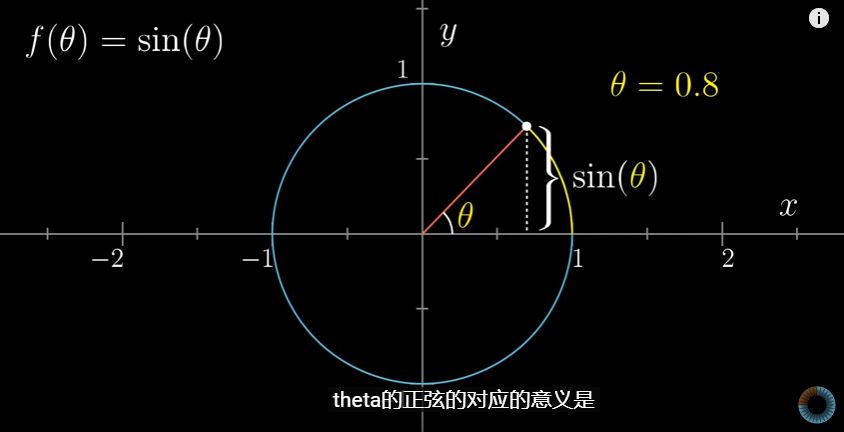
让我们再来更吊的函数,正弦函数,sin(θ)
我们先定义上面的那副图,首先圆的半径是 1,θ 就是在圆上走的路径距离。
sin(θ) = 所在点的高度。
点不断地在圆上走动,我们的 sin(θ) 就会出现一个波动的图像,如果我们取每一个点的斜率,我们也会发现他们的值也是波动性的。
根据我们的导数公式,我们可以知道:
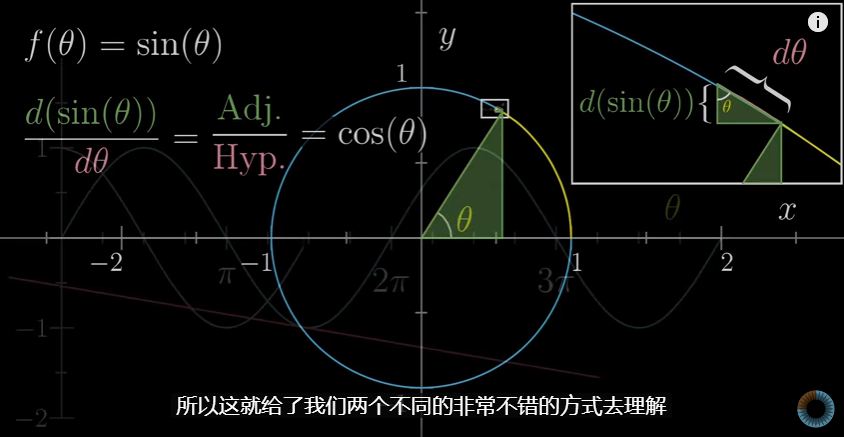
d(sin(θ)) / d(θ) = cos(θ)但是,我们是怎么确定它的斜率是 cos(θ) ?
上面那个圆的半径是 1。
我们知道在圆上走 θ ,这段圆弧对应的圆角是 θ 度,其高度就是 sin(θ),假设圆弧向上又走了一段距离,也就是 dθ ,因为距离非常的短,所以,这个多余的距离又可以当做一条直线。
如上图的右上角所示,此时其高度对应于 d(sin(θ)) .
根据三角形相似的原理,我们可以得知小三角的一个角是 θ ,也就是图中所示。
所以,根据小三角形的式子 d(sin(θ))/dθ = cosθ
OK,原理现在已经清楚了。