如题。。。另外,我怎么记得我之前好像写过类似的。
我们为什么需要激活函数,那是因为现实是很复杂滴。。。
假如说,一个女生特别漂亮,嘿嘿,那应该是有很多男生喜欢,越漂亮就越多人喜欢,可能如下图:
我们计算机可能会处理线性方程,当然,你也可能会说计算机也可以处理非线性方程,但是,对于计算机来说,处理一个非线性问题最好的办法就是用多个线性函数共同描述。
OK,那我们如何将线性问题转化为非线性呢?此时,就是激活函数登上舞台了。
所谓的激活函数,就是给线性添加了一个壳,从而掰弯它。。。
y = W * x
y = AF( W * x)
其中,AF 就是激活函数那么 AF 就是一种非线性方程而已。
从知乎上看了一个蛮不错的解释,下面分享过来。
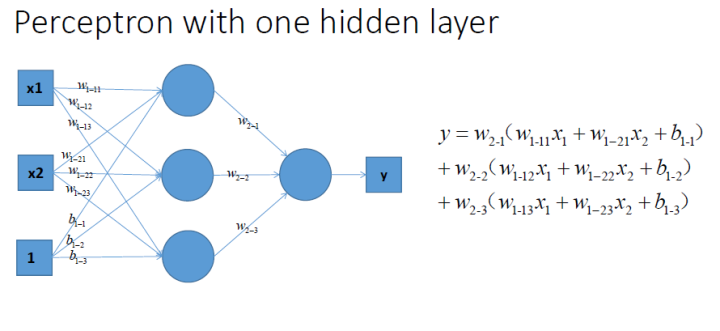
这是一个单层的感知机, 也是我们最常用的神经网络组成单元啦. 用它可以划出一条线, 把平面分割开。

那么很容易地我们就会想用多个感知机来进行组合, 获得更强的分类能力, 这是没问题的啦

那么我们动笔算一算, 就可以发现, 这样一个神经网络组合起来,输出的时候无论如何都还是一个线性方程哎,纳尼, 说好的非线性分类呢!!???
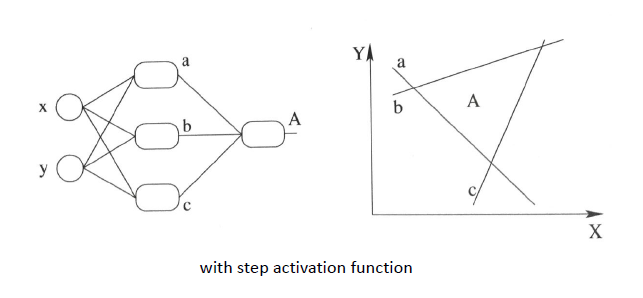
再盗用一幅经常在课堂上用的图…然而我已经不知道出处是哪了, 好像好多老师都是直接用的, 那我就不客气了嘿嘿嘿,这幅图就跟前面的图一样, 描述了当我们直接使用step activation function的时候所能获得的分类器, 其实只能还是线性的, 最多不过是复杂的线性组合罢了,当然你可以说我们可以用无限条直线去逼近一条曲线啊……额,当然可以, 不过比起用non-linear的activation function来说就太傻了嘛….
祭出主菜. 题主问的激励函数作用是什么, 就在这里了!!
我们在每一层叠加完了以后, 加一个激活函数, 如图中的y=sigma(a). 这样输出的就是一个不折不扣的非线性函数!

于是就很容易拓展到多层的情况啦, 更刚刚一样的结构, 加上non-linear activation function之后, 输出就变成了一个复杂的, 复杂的, 超级复杂的函数….额别问我他会长成什么样, 没人知道的我们只能说, 有了这样的非线性激活函数以后, 神经网络的表达能力更加强大了(比起纯线性组合, 那是必须得啊!)

继续厚颜无耻地放一张跟之前那副图并列的图, 加上非线性激活函数之后, 我们就有可能学习到这样的平滑分类平面. 这个比刚刚那个看起来牛逼多了有木有!

典型的激活函数
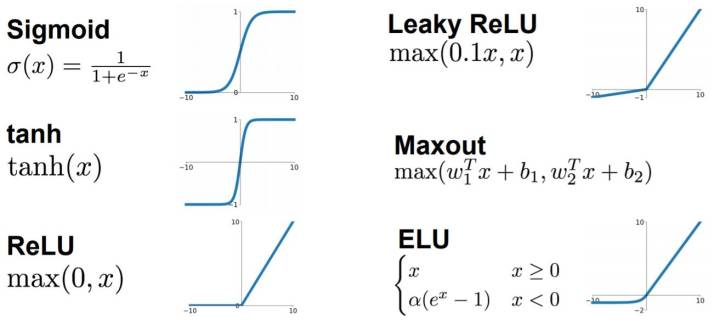
事实上,我们也可以创造自己的激活函数,但必须保证创造的激活函数是可以微分的。因为在反向传播中我们需要微分来传递误差。
那这个激活究竟是什么意思?
首先我们应该知道,神经网络对于特征是有偏置的,也就是说,如果识别一张图片是不是人,那么手可能就是重点识别区域。
我们以 sigmoid 激活函数为例。我们看到当 x 向负数的方向移动的时候,我们的值是越来越小的,所以,这部分的特征值不是重点,但是如果 x 的权值很大,导致 sigmoid 出来的值接近于 1,那么就证明这个特征确实十分重要,它也就相应的被激活了。
OK,现在你是不是又有一个疑问,那就是激活函数用在哪里?
假设,我们有一个输入,两个隐藏,一个输出。
我们对于第一个隐藏,会得到一种 W 和 b,于是我们得到后会 WX1 + b,但是我们的激活函数也是对所求的函数进行激活,从而得到比较重要的特征。
所以第一隐藏层传到第二隐藏层的时候,会加上激活函数,最后应该是 y = AF(WX1 + b)。
我们第二个隐藏层再对 y 进行处理,得到函数 Z = W2y + b2
当把数传到输出层的时候,我们再添加激活函数。
AF(W2y + b2)
经过激活函数求解后输出的是大都是概率。
现在我们已经了解了激活函数了,但是激活函数这么多,我们应该什么时候使用哪种激活函数?
激活函数的应用场景
非线性激活函数有 Sigmoid、Tanh、ReLU、LReLU、PReLU、Swish 等。
下面我将推荐几个极好的文章。
sigmoid
其函数形式如下:

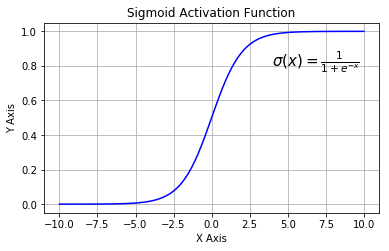
其导数图像

Sigmoid 函数的三个主要缺陷:
梯度消失:注意:Sigmoid 函数趋近 0 和 1 的时候变化率会变得平坦,也就是说,Sigmoid 的梯度趋近于 0。神经网络使用 Sigmoid 激活函数进行反向传播时,输出接近 0 或 1 的神经元其梯度趋近于 0。这些神经元叫作饱和神经元。因此,这些神经元的权重不会更新。此外,与此类神经元相连的神经元的权重也更新得很慢。该问题叫作梯度消失。因此,想象一下,如果一个大型神经网络包含 Sigmoid 神经元,而其中很多个都处于饱和状态,那么该网络无法执行反向传播。如果你的初始值很大的话,大部分神经元可能都会处在saturation的状态而把gradient kill掉,这会导致网络变的很难学习。
不以零为中心:Sigmoid 输出不以零为中心的。
计算成本高昂:exp() 函数与其他非线性激活函数相比,计算成本高昂。
Tanh

其导数图像
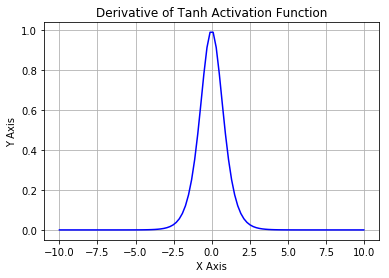
Tanh 激活函数又叫作双曲正切激活函数(hyperbolic tangent activation function)。与 Sigmoid 函数类似,Tanh 函数也使用真值,但 Tanh 函数将其压缩至-1 到 1 的区间内。与 Sigmoid 不同,Tanh 函数的输出以零为中心,因为区间在-1 到 1 之间。你可以将 Tanh 函数想象成两个 Sigmoid 函数放在一起。在实践中,Tanh 函数的使用优先性高于 Sigmoid 函数。负数输入被当作负值,零输入值的映射接近零,正数输入被当作正值。唯一的缺点是:
Tanh 函数也会有梯度消失的问题,因此在饱和时也会「杀死」梯度。
为了解决梯度消失问题,我们来讨论另一个非线性激活函数——修正线性单元(rectified linear unit,ReLU),该函数明显优于前面两个函数,是现在使用最广泛的函数。
修正线性单元(ReLU)
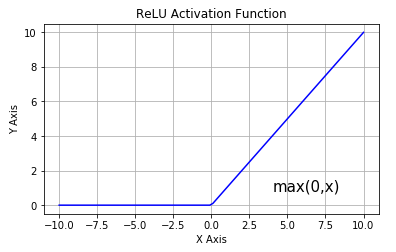
其导数图像
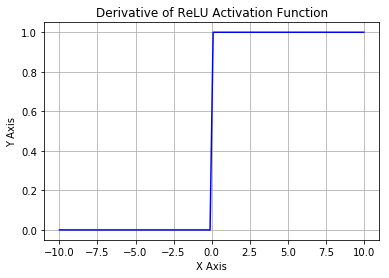
从上图可以看到,ReLU 是从底部开始半修正的一种函数。数学公式为:

当输入 x<0 时,输出为 0,当 x> 0 时,输出为 x。该激活函数使网络更快速地收敛。它不会饱和,即它可以对抗梯度消失问题,至少在正区域(x> 0 时)可以这样,因此神经元至少在一半区域中不会把所有零进行反向传播。由于使用了简单的阈值化(thresholding),ReLU 计算效率很高。但是 ReLU 神经元也存在一些缺点:
不以零为中心:和 Sigmoid 激活函数类似,ReLU 函数的输出不以零为中心。
前向传导(forward pass)过程中,如果 x < 0,则神经元保持非激活状态,且在后向传导(backward pass)中「杀死」梯度。这样权重无法得到更新,网络无法学习。当 x = 0 时,该点的梯度未定义,但是这个问题在实现中得到了解决,通过采用左侧或右侧的梯度的方式。
为了解决 ReLU 激活函数中的梯度消失问题,当 x < 0 时,我们使用 Leaky ReLU——该函数试图修复 dead ReLU 问题。下面我们就来详细了解 Leaky ReLU。
Leaky ReLU
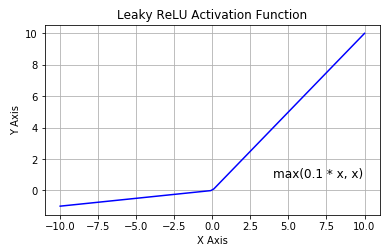
该函数试图缓解 dead ReLU 问题。数学公式为:
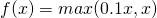
Leaky ReLU 的概念是:当 x < 0 时,它得到 0.1 的正梯度。该函数一定程度上缓解了 dead ReLU 问题,但是使用该函数的结果并不连贯。尽管它具备 ReLU 激活函数的所有特征,如计算高效、快速收敛、在正区域内不会饱和。
Leaky ReLU 可以得到更多扩展。不让 x 乘常数项,而是让 x 乘超参数,这看起来比 Leaky ReLU 效果要好。该扩展就是 Parametric ReLU。
Parametric ReLU
Parametric ReLU的数学公式:
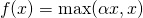
其中是超参数。这里引入了一个随机的超参数,它可以被学习,因为你可以对它进行反向传播。这使神经元能够选择负区域最好的梯度,有了这种能力,它们可以变成 ReLU 或 Leaky ReLU。
总之,最好使用 ReLU,但是你可以使用 Leaky ReLU 或 Parametric ReLU 实验一下,看看它们是否更适合你的问题。
Swish

该函数又叫作自门控激活函数,它近期由谷歌的研究者发布,数学公式为:

根据论文(https://arxiv.org/abs/1710.05941v1),Swish 激活函数的性能优于 ReLU 函数。
根据上图,我们可以观察到在 x 轴的负区域曲线的形状与 ReLU 激活函数不同,因此,Swish 激活函数的输出可能下降,即使在输入值增大的情况下。大多数激活函数是单调的,即输入值增大的情况下,输出值不可能下降。而 Swish 函数为 0 时具备单侧有界(one-sided boundedness)的特性,它是平滑、非单调的。更改一行代码再来查看它的性能,似乎也挺有意思。