动态规划是一种牛逼闪闪的算法思想。
先上维基百科的解释:
动态规划背后的基本思想非常简单。大致上,若要解一个给定问题,我们需要解其不同部分(即子问题),再根据子问题的解以得出原问题的解。
通常许多子问题非常相似,为此动态规划法试图仅仅解决每个子问题一次,从而减少计算量:
一旦某个给定子问题的解已经算出,则将其记忆化存储,以便下次需要同一个子问题解之时直接查表。
这种做法在重复子问题的数目关于输入的规模呈指数增长时特别有用。OK,现在我们从著名的 Fibonacci Sequence.
Fibonacci Sequence
凡人的做法
F(N) = F(N - 1) + F(N - 2)
if N == 1 or N == 0 :
return 1即用递归的思想,但是用递归就会有有一种冗余的存在,请看下面这幅图。

但是很明显左边的分支 F(5) 和右边的分支 F(5) 是同一值,但是,我们却需要计算很多次,所以我们做的全是重复的工作。
但是,如果我们只计算一次 F(5) ,然后记录他的值,如果后期再遇到的话可以直接返回值。
按这个方法得到的时间复杂度是 O(2 ^ n)
斐波那契之动态规划
我们倒着推。
我们知道
F(1) = 1
F(2) = 1
F(3) = 2
F(4) = 3
... ...我们事先知道 F(1),F(2) ,如果要求 F(3) ,那就直接用 F(1) + F(2)。
如果要知道 F(4) 只需 F(3) + F(2)
我们如果是从头向后推,那么我们的时间复杂度是 O(n)。
这时候,我们就有个疑问,这不是小孩子的算法吗?和动态规划有什么联系。
但是,这种算法的隐含了一个条件,就是记忆功能,没得出一个数值,这个数值都隐含了前面的信息。
懵不懵逼,来,勇士,不要着急,再来一局。
如何快速赚大钱
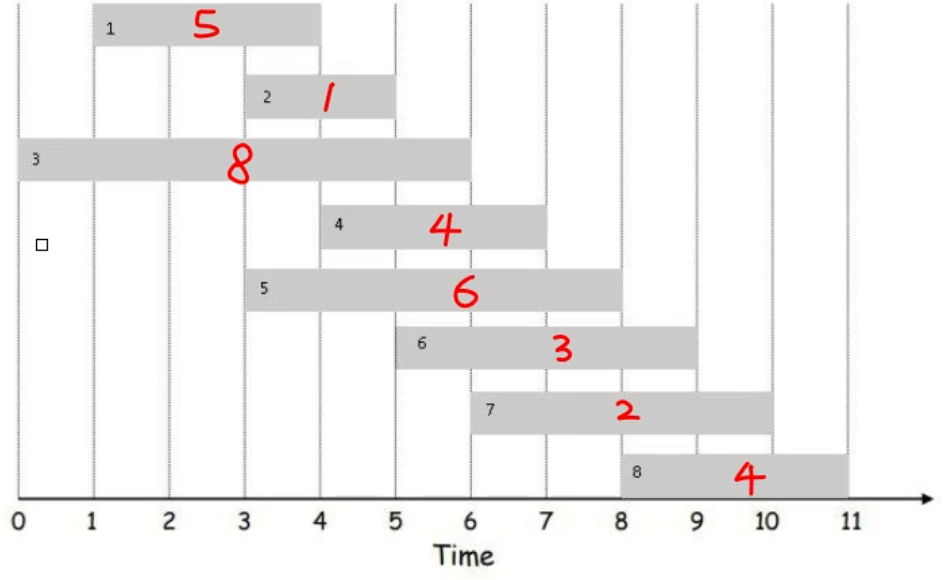
图中一共有 8 分工作,矩阵的长度代表着这个工作的时长,并且有开始和结束的信息。
一个人在同一时间只能做一份工作。
红色的数字是这个工作能赚多少钱。
而,我们的问题是,如何选择才能达到利益最大化?
在做这个题之前,我们先行规定一些变量和其所代表的意义。
OPT(i) 代表的是做第 i 个工作的时候,能获得的最大的报酬
prev(i) 表示我非得做第 i 个工作后还有几个工作
这个非得并不是我做 8 后还能做 7,比如 prev(8) 代表的是 5,即我非要做第 8 个工作,所以,以后我只能选择前 5 个工作
prev(7) = 3
prev(6) = 2
...
prev(2) = 0 对于 OPT(i) 我们一共有两个选择,就是选这个和不选这个。
如对于 OPT(8) 来说,选的话就是 4 + OPT(5)
意思就是第八个工作的报酬是 4 ,如果做了第八个,就只能从前 5 个工作选。
不选的话就是 OPT(7)
做成图
OPT(8)
选 : 4 + OPT(5)
不选 : OPT(7)我们现在再列一个表格
i prev(i)
1 0
2 0
3 0
4 1
5 0
6 2
7 3
8 5我们来从头计算 OPT
OPT(1) 我们没有选择,只能做第 1 个工作,所以 OPT(i) = 5
我们现在有一下的列表:
i prev(i) OPT(i)
1 0 5假如是 OPT(2) 我们有两个选择,就是选择做工作 2 ,然后 OPT(2) = 1 + prev(2) = 0
或者不选工作 2,OPT(2) = OPT(1) = 5
所以,表格更新为:
i prev(i) OPT(i)
1 0 5
2 0 5再举一个特殊例子:
OPT(4)
我们已经知道下面这个表格
i prev(i) OPT(i)
1 0 5
2 0 5
3 0 8OPT(4) 同样也面临两个选择,一个是 OPT(3) 或者 4 + prev(4) = 4 + OPT(1) = 9
所以,表格更新为:
i prev(i) OPT(i)
1 0 5
2 0 5
3 0 8
4 1 9到此,我们就已经知道下面的步骤了。最终的表格如图所示:
i prev(i) OPT(i)
1 0 5
2 0 5
3 0 8
4 1 9
5 0 9
6 2 9
7 3 10
8 5 13这样不断的将自身的记忆传承,使得求解问题变的简单。