这是一个非常有意思的算法。
场景模拟
我们设想这样一个场景,在偌大的地方,有一个区域存放着食物,天空中环绕着一群鸟。这些鸟都不知道食物在哪里,但是他们却知道离食物有多远。(逻辑有点反人类,但是就是这么一个场景)
因为知道和食物之间的距离,所以,离食物越近的地方,鸟越多,而后面的鸟为了更快的找到食物,应该优先向鸟多的地方靠近。所以,最后鸟们跟着趋势都能找到食物。
我们就将鸟比较粒子,每个粒子都有动力,也就是相当于鸟的速度,然后,粒子和紧邻的优等粒子模仿,
公式讲解
PSO 初始化一群随机粒子,然后叠代找到最优解。每次叠代,粒子都会找两个极值来更新自己。第一个极值是粒子自身的极值 pBest,也就是很多代中粒子表现最好的数值,第二个极值是 gBest 整个种群的最优解。
如图所示:

上面的加和为矢量加。
每个粒子的位置和速度都以随机方式进行初始化,而后粒子的速度就超着全局最优和个体最优的方向靠近。

看图是不是很懵逼,我也是。。。但是,可以知道的事,图中传递的一个信息是矢量相加。

对于粒子速度的更新公式,我们可以分为三个部分。
第一个部分: 粒子的当前速度对粒子飞行的影响,这部分提供了粒子在搜索空间的飞行动力。
第二部分是所谓的个体认知部分,代表了粒子的个人经验,简单一点来说,这个就是垂直搜索,一个样本自身有很多代,每一代都有一个参数,这些参数中必然有一个最优的值,所以, pBest 就是历史上,粒子自身的最优值。
第三部分是所谓的群体认知,代表了群体经验对粒子飞行轨迹的影响,促使粒子朝着群体发现的最好的位置移动。


对 PSO 的改进
加惯性权重


事实上,几乎大部分的粒子群算法都是按这个公式来写的。
加收缩因子

其它改进方法
改进方法有很多,比如和雁群结合,和退火算法结合等等
算法边界条件

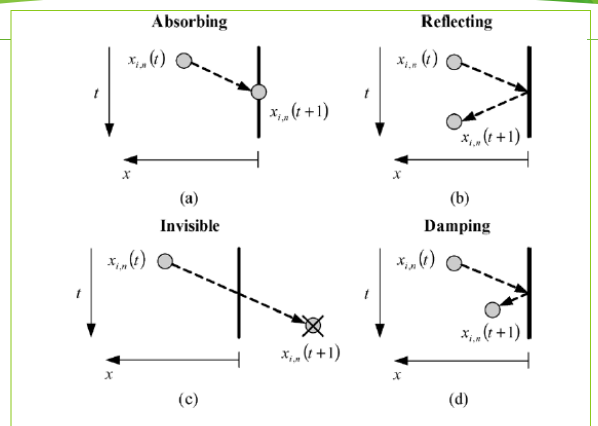
有一篇论文就是专门论述这四种墙哪种最好,先说结论结论,是阻尼墙最好,这也可以用现实生活中的例子说明。
大学课堂有一个学生每次都逃课,授课教授一共有四种方法,第一种继续不管他,但是最后成绩给它挂科,相当于吸收墙,第二种,继续不管他,但是最后成绩给他通过,即便他没有考试,这是反射墙,第三种直接无视他,爱怎么样就怎么样,第四种,给他惩罚措施,但是让他回来上课,相当于阻尼墙。
所以,只有第四种逃课学生才能学到知识。