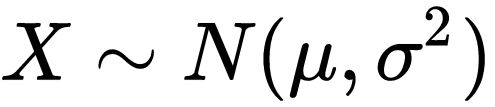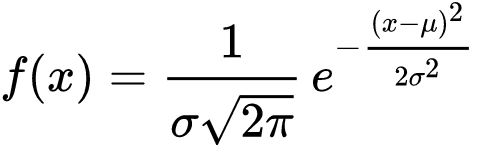这篇主要讲述正态分布。
什么是正态分布
从数学的角度
若随机变量 X 服从一个位置参数为 μ 尺度参数为 σ 的正态分布,记为
则其概率密度函数为:
正态分布的数学期望值或期望值 μ 等于位置参数,决定了分布的位置;其方差 σ ^ 2的开平方或标准差 σ 等于尺度参数,决定了分布的幅度。
正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线(类似于寺庙里的大钟,因此得名)。我们通常所说的标准正态分布是位置参数 μ =0,尺度参数 σ ^ 2 = 1的正态分布
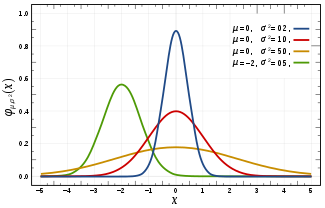
从生活的角度
其实,日常生活中无处不是正态分布,比如人的身高、收入等等。

从编程的角度
我们经常会遇到随机一些正态分布的数,这些正态分布的数是指更加接近自然分布的数,即中间的数据多,而边上的数据少。
浅度解析
中心极限定理
中心极限定理是概率论中的一组定理。中心极限定理说明,在适当的条件下,大量相互独立随机变量的均值经适当标准化后依分布收敛于正态分布。
知乎上的回答
正态分布的的普遍性可以中心极限定理得到。直白地说,如果一个指标受到若干独立的因素的共同影响,且每个因素不能产生支配性的影响(Lindeberg 条件),那么这个指标就服从中心极限定理,收敛到正态分布,这就是林德伯格-费勒中心极限定理的意思。举个例子,学生的成绩(指标)受许许多多因素影响诸如状态、能力、心情等等充分多的因素影响,成绩的形成是许多因素影响的加总。这些因素没有一个能够支配性地影响成绩,那么即使这些因素各自都不是正态分布的,它们所形成的成绩也是正态分布的。