这篇文章可以算是机器学习的入门课程,全篇不会写一点代码,完全就是将大致的思路写一遍。
如果可以比拟的话,我想这篇就好像我们写程序时候的 “hello world”。
其实上面的链接已经讲得很清楚了,之所以写这篇还是为了以后装逼。
万一哪天有人问起:丛哥,机器学习怎么入门?
我就可以把手一挥,冲他神气的说道:看看我写的文章。QvQ。
很期待这一天,哈哈。
什么是 MNIST?
MNIST 就是一个手写数字的数据集。我们都知道,机器中只有 0 和 1,但是要表现电脑中的图像,汉子,也只不过是特定的像素点是 0 还是 1 而已。
当然,MNIST 只是个数据集,就是你自己也可以创造,所以,假定每个数字都由 28 * 28 个像素点组成,每一个为 1 的像素点组成一个数字。如下图:
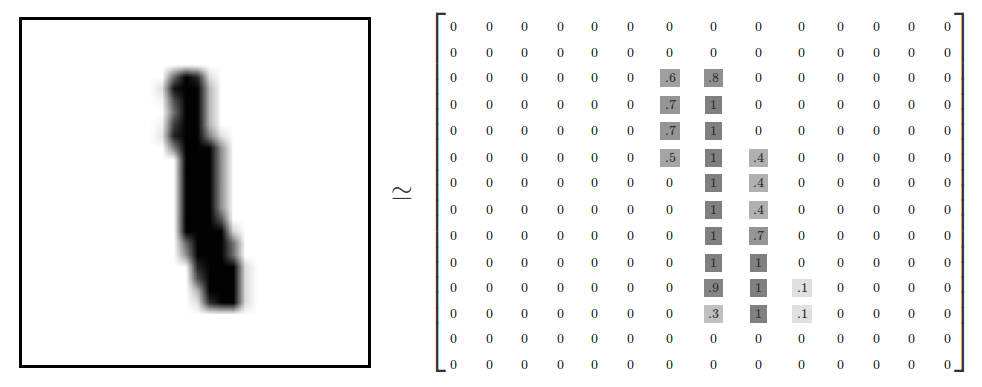
当然,这个数据集中不仅仅只是包含像素数字而已,还包含数字的标签,因为电脑看过去只是 0 或者 1,所以我们要对每一个像素数字贴上一个标签,讲述它到底是数字几。
比如,标签0将表示成([1,0,0,0,0,0,0,0,0,0])。
所以,现在 MINST 就有两个数据包了,一个是像素数字,另一个是标签数字。
假如像素数字有 6000 个,即二维数组 6000 * 784 ,那么数字标签则是 6000 * 10。
但是,但凡有点逻辑思维的人都知道,测试一个东西要用新的测试,而不是用旧的测试。
所以,数据集又可以再分为训练数据集和测试数据集,这两个数据集应该是没有交集的。
训练数据集用来训练出函数,而测试数据集则用来检测函数的拟合程度。
训练数据的原理
如果,一个对机器学习毫无接触的人来想象如何训练电脑认识书写数字,我想他的第一反应是懵逼。
毕竟,电脑只是机器而已,又不是人类,能都逻辑判断。
其实相较于人类的逻辑判断,电脑更适合计算。
我们人类在看见抛出去的东西都再次坠落到地面后,当我们判断一个物体脱离手之后,那一定会想到它最后会回到地面。当然,这里面有一定的大数据的思想,但是,多次观看物体坠落地面,我们人类也自然懂得了这个常识。
如果变成机器来学习,就会成为,给出重力加速度,高度,时间等相关参数,在进行函数运算后,得到会回到地面的结果。
其实,机器学习和人类学习并没有绝对的界限,只不过是看问题的角度不同。
就好比,生物认为人类是细胞组成,化学认为人类是元素组成,哲学认为我思故我在,物理主张粒子,数学主张计算。虽然,各有各的说法,但是人类是所有学科的综合。
所以,机器学习也是在学习人类的一部分,就是数学,只不过,电脑的计算能力表面上比人类强。(实际上,计算能力连一个单细胞生物都比不上)
额,说了这么多的废话。
当机器在学习数据的时候,就会分辨出数据中蕴含的重力加速度,高度,时间等参数,再根据相应的函数来判断是否落到地面。
那么机器如何推导出参数?
当你看见 1 的时候,你的大脑会 100 % 确定是 1。这里的重点在于,你判断一个数是什么的概率,如果有人写字很丑,将 6 和 8 写的差不多,你的判断就不会这么迅速,就会想,这个到底像 6 还是像 8。
换成计算机来看就是,这个数到底是 6 的概率大,还是 8 的概率大。
计算机通过我们给的数据,经过函数计算得到最终谁的概率大。
如何计算函数
我们再看一下这个图:

当像素点为 1 的时候,这个点的比重或者说权重就大,毕竟这个像素点是组成数字的一部分。
当数以万计的相同数字集合,即便是同一数字,因为每个数字因为长得不一样,导致相同数字最后的样子集合变的更为臃肿,如下图:
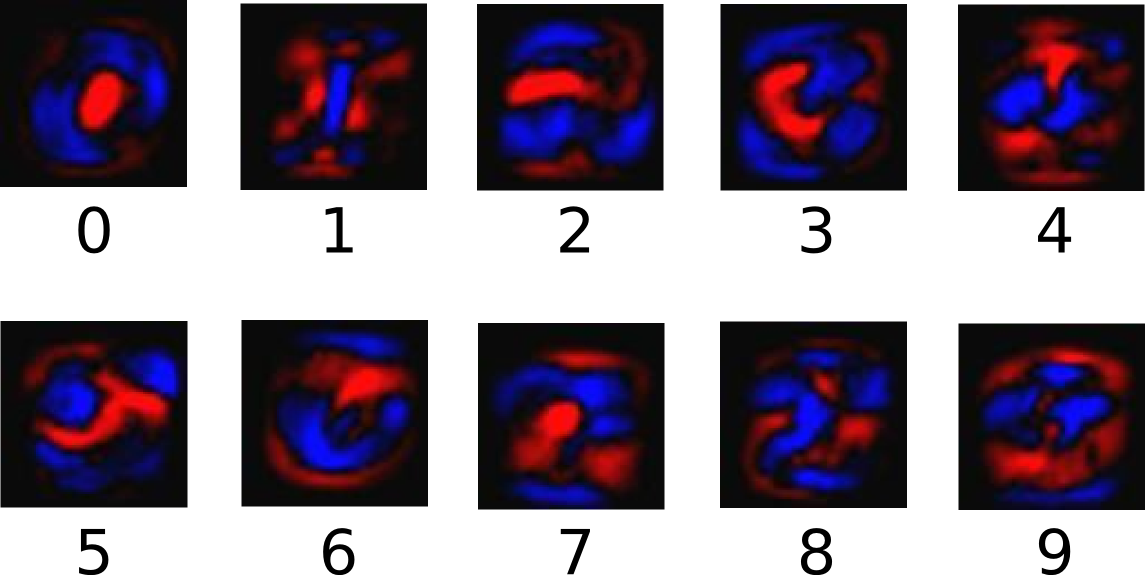
红色代表负数权值,蓝色代表正数权值。
我们对同一个数字分析,因为每一点的权重不一样,所以我们将每一点对应的权重设为 Wi ,那个像素点就代表 Xi。
所以,计算综合在一起,一个图片的权重和为:
Y = Wi * Xi (i = 0,1....783)
但是,函数本身存在偏差,所以引入一个常数项减小偏差
Y = Wi * Xi + b (i = 0,1....783)最后的结果是:
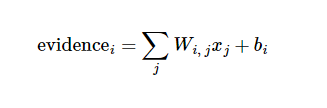
但是,我们计算的这个数值,肯定不是概率数值,甚至有可能数值会达到万级以上,所以,我们需要再次进行包装,让最后的数字以概率的形式出现。
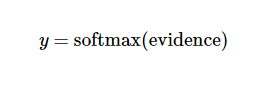
其中, softmax 就是包装,在机器学习中又叫激活函数。(完全不懂为什么叫这个破名字?抖机灵???)
所以,计算这些数的概率就如下图所示:

将其写成一个等式:
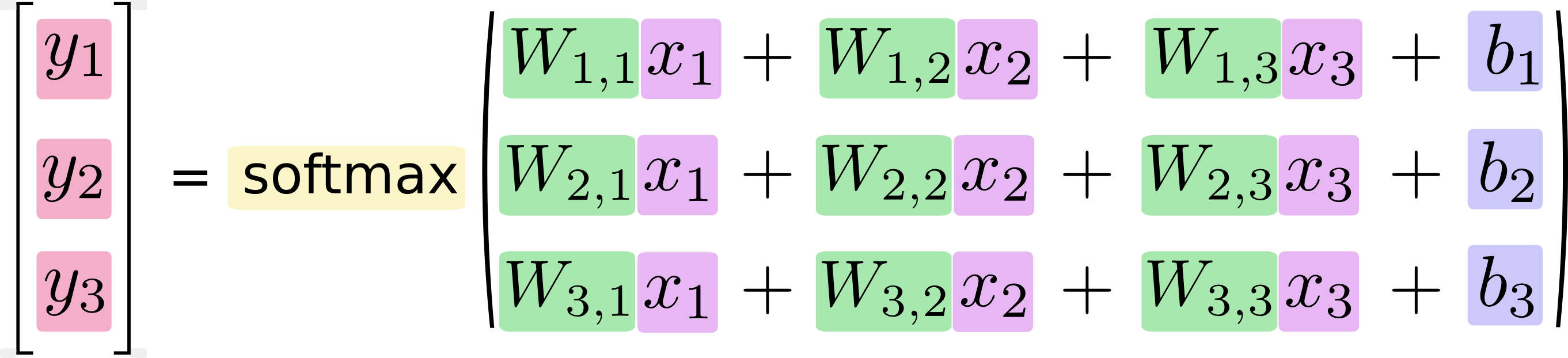
让我们继续装逼,写成向量的形式:

最终,哪个数的的概率大就是哪个数。
好了,装逼结束,打完收工。