纵观各种辅导书和各种视频对 KMP 的解析,我只想对他们说:真是**了狗了。
但是,每个人解读的角度不同,所以,别人看我的解析,也可能会是上述感觉。
首先,我们要理解 KMP,就要先要理解暴力拟合。
数据定义
TXT 原数据
STR 要拟合的数据
暴力拟合
顾名思义,暴力拟合就是穷举,只不过标记在 TXT 上,首先标记 i 指向 TXT 的开头。
如果拟合不成功,则 i += 1,直到拟合成功。
这种算法的时间复杂度是 O(M * N)。 [M 代表 TXT 的长度, N 代表 STR 的长度]
KMP
上述算法是非常消耗时间的,有一天,大佬突发奇想,如果标记不在 TXT 上,而是从 STR 取得坐标,那岂不是更好。
所以, KMP 的标记是对 STR,而不是 TXT。
要理解标记,首先应该理解 PMT(部分匹配表)。
另外对于 KMP 来说,时间复杂度是 O(M + N)[ M = len(TXT) , N = len(STR)]。
空间复杂度为 O(N)。
PMT
前缀和后缀
对于 aba 来说:
前缀包括:[a , ab]
后缀包括:[a , ba]
很明显前缀和后缀中交集最长的长度是 1,即[a]。
PMT 中的数值,是从头到尾,前缀和后缀交集中最长的长度。
对于数据:
a a b c a a b b b a a
PMT 0 1 0 0 1 2 0 0 0 1 2事实上 PMT 根本没什么卵用,真正有用的是它的变种 next 数组。
next数组
next 数组和 PMT 其实区别不大,只不过 next 数组取的是标记前面的前缀和后缀交集中最长的长度。
比如: abab 标记在最后的 b 上。
则比较的是 aba 中的前缀和后缀交集中最长长度。
即 1,所以最后的 b 对应的是 1。
a b a b
1其实很多参考书,将 next 数组中的数值,在原有得数的基础上 + 1[得到 PMT]。我认为他们这是在脱裤子放屁。
其实 PMT 和 next 的得数的区别在于 PMT 后移一位得到 next,next 的初始位置补 -1。
a a b c a a b b b a a
PMT 0 1 0 0 1 2 0 0 0 1 2
next -1 0 1 0 0 1 2 0 0 0 1那么 next 数据如何进行匹配呢?
观看下一幅图:
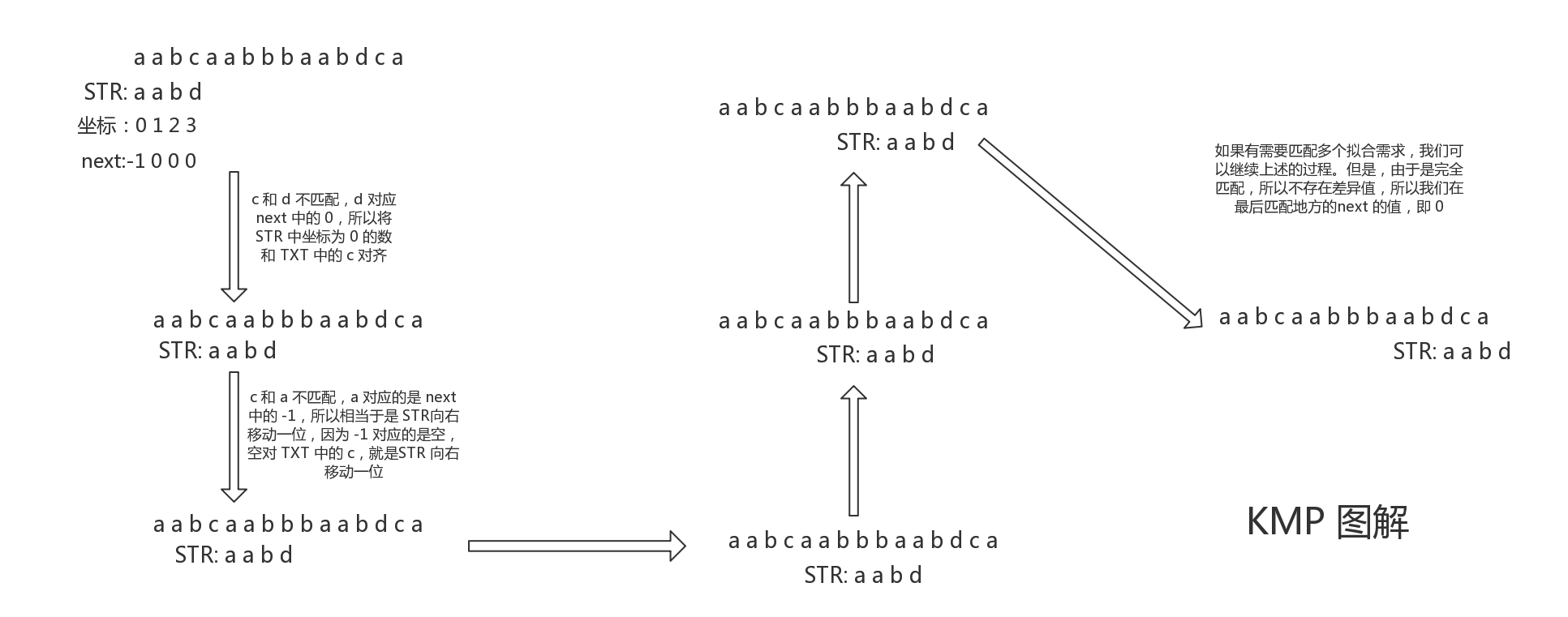
我们现在知道如何移动以及匹配了,那么新的问题来了,为什么这样移动就可以成功?
why
还是举例子说明
TXT: a a c c a a b b b a a
STR: a a b
next: -1 0 1
上面是 c 和 b 不同,也就是说 TXT 之前的数据和 STR 之前的数据是相同的。
换句话说:TXT 中 a a c 的后缀 a ,和 STR 中 a a b 的前缀 a 是相同的。
所以拿着 STR 的前缀对上 TXT 中的后缀当然是符合的。回溯原理:

代码
原理讲完了,应该上代码了。
首先是 next 代码,在此之前再上一个图。
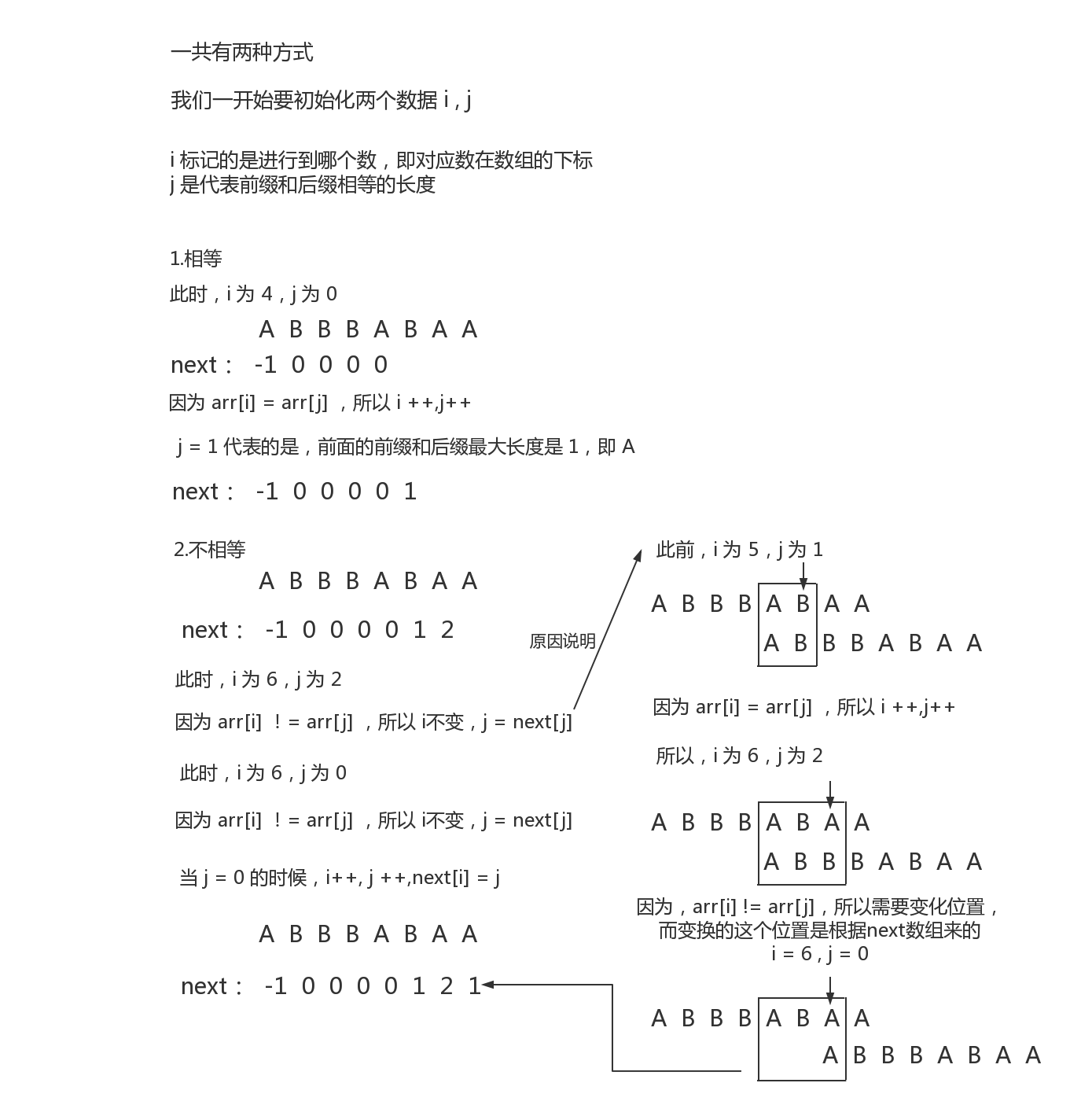
next
1 | def getNext(substr,next): |
KMP
1 | def KMP(str,substr,next): |
测试
1 | sub = "abc" |