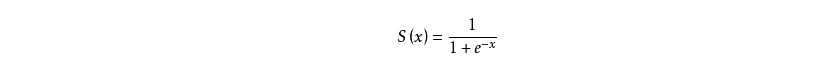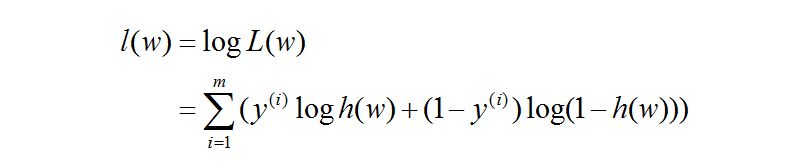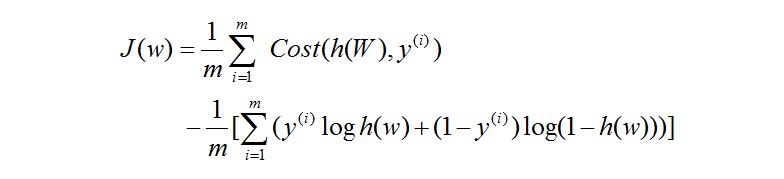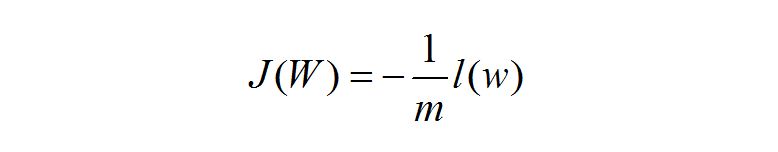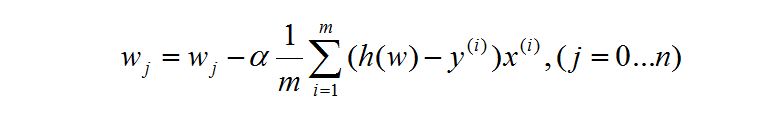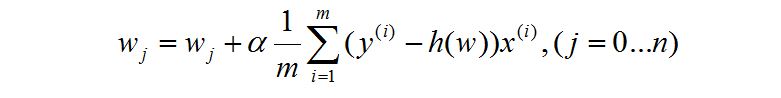姑苏城外一茅屋，万树梅花月满天

0%

Logistic回归

发表于 更新于 分类于 ， ， Valine：

github

Logistic回归又叫逻辑回归，虽然有回归二字，但却是一个分类算法。

参考资料

事实上，我在这里想说一下关于 Logistic 回归的信息来源。最初我是在 Andrew Ng 教授的网课上了解的，他用的是梯度下降，后来又读了周志华老师的《机器学习》和 Peter 的《Machine Learning in Action》。

我想凡是这样经历的人都有疑问，为什么到了《in Action》 用的却是梯度上升。

其实，梯度下降和《in Action》梯度上升完全是一回事，我甚至觉得在《in Action》 中， Peter 老师可能写错了。

至于为什么，你可以在我的这篇博文中找到答案，但是现在让我们回到开头。


介绍


我们以二分类为例，所以最后的分类结果我们可以用 0 或者 1 来代替。

所以，我们理想的函数是这样的，我们输入输入项之后，有一个函数可以输出 0 或者 1 。在这里先介绍海维赛德阶跃函数。

但是这个函数有一个明显的缺点，就是从 0 直接跃到 1，这个瞬间跳跃很难处理，因为即便是数据再怎么浩瀚，一个预测值最终只能是概率预测，而不是绝对的分类预测，所以我们引入 sigmoid 函数。

sigmoid 函数如下：

其函数图像如下：

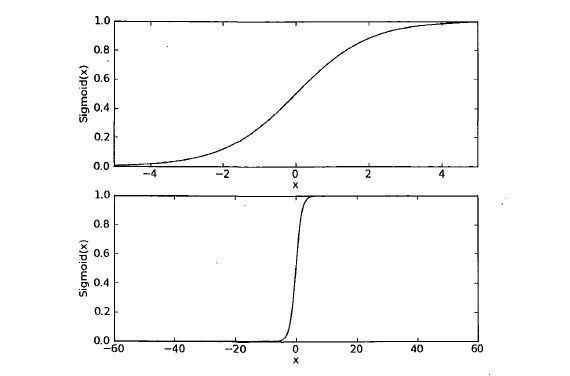
我们是这样安排的，每一个特征乘以一个回归系数，然后所有的结果相加，即 W’X ，再将这个总和代入 sigmoid 函数中，进而得到范围为 0 - 1 之间的数值。

将大于 0.5 的归于 1，将小于 0.5 的归于 0。

而正像上图所示，当 X 值很大的时候， sigmoid 函数也就表现的和海维赛德阶跃函数一样了。

梯度下降和梯度上升

所以，我们下一步的首要任务是如何找到最佳的 W。

梯度下降

首先我们要介绍 Andrew Ng 教授的梯度下降。

数学原理

我们设函数 F(x) ，假设函数是一个正 U 型。如下图所示：

我们如何在曲线上选一个点，然后用某种手段到达最低点？

假设我们的点 x1 在曲线的右边，那么我们对 F(x1) 求导，得到这点位于曲线上的导数(斜率)。最后我们得到下面这个式子：

其中 a 为学习率，为正数，因为点在曲线右边，所以斜率为正，原 W 是一个正数，所以正数减去一个正数，所以点最后向左边移动。

假设点在曲线左边，那么斜率为负，而此时的 W 是一个负数，一个负数加上一个正数，点向右移动。

所以无论怎样最终都向最低点移动。如果移动到最低点，因为斜率为 0 ，所以以后再怎么迭代也不会改变 W 了。

但是我们有一个疑问点，那就是图像中的 J 是什么？

误差 J

假设我们的预测函数为 Z(x) = w1 * x1 + w2 * x2 + … + wn * xn

然后我们运用 sigmoid函数，得到下面的式子：

而上面的 h(w) 就是最终的我们要预测分类的式子。

h(w)函数的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

上述式子可化为：

对数似然函数为：

所以，我们根据上面推出：

误差 J：

于是上面式子我们可以得出：

求 J 的最小值

可用下面公式：

而这个公式的难点在于求导数。

过程在这里不表述，要是感兴趣可以看下面的链接：

参考资料

我直接写出最后的答案。

我们都知道对于上述式子乘不乘 1/m 对图像都没有影响。

此时，我们的梯度下降原理就已经写完了。

梯度上升

说实话，当你理解了为什么这个叫梯度上升的时候，我想你会激动地想骂人。

我们直接看 《in Action》 中的式子：

它之所以叫梯度上升，是因为相对于梯度下降这个式子将中间减号改为加号，但是为什么改为加号呢？

是因为它括号里面的式子减数和被减数交换了位置，所以，这就是安安全全的梯度下降式子。

所以，我觉得要么是作者的失误，要么是翻译的人嗑药了。

所以在 《in action》中用的是伪梯度上升。

关于梯度下降的注意点

梯度下降是为了找寻最低点，如下图所示：

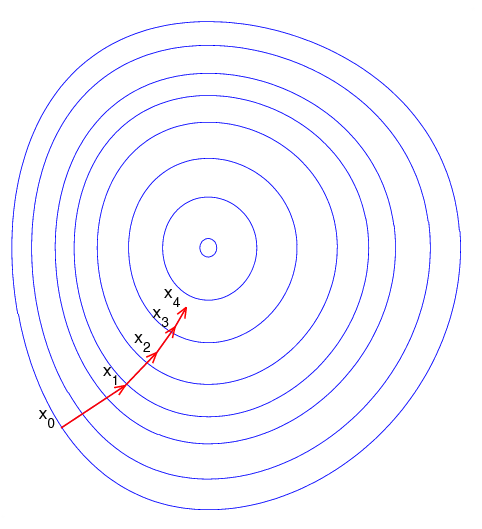
图中圆圈代表的是等高线。

其实梯度下降往往找的不是最低点，因为目标函数的复杂导致图像是由多个凹图像组成，最终我们找的是局部最小值，如图所示：

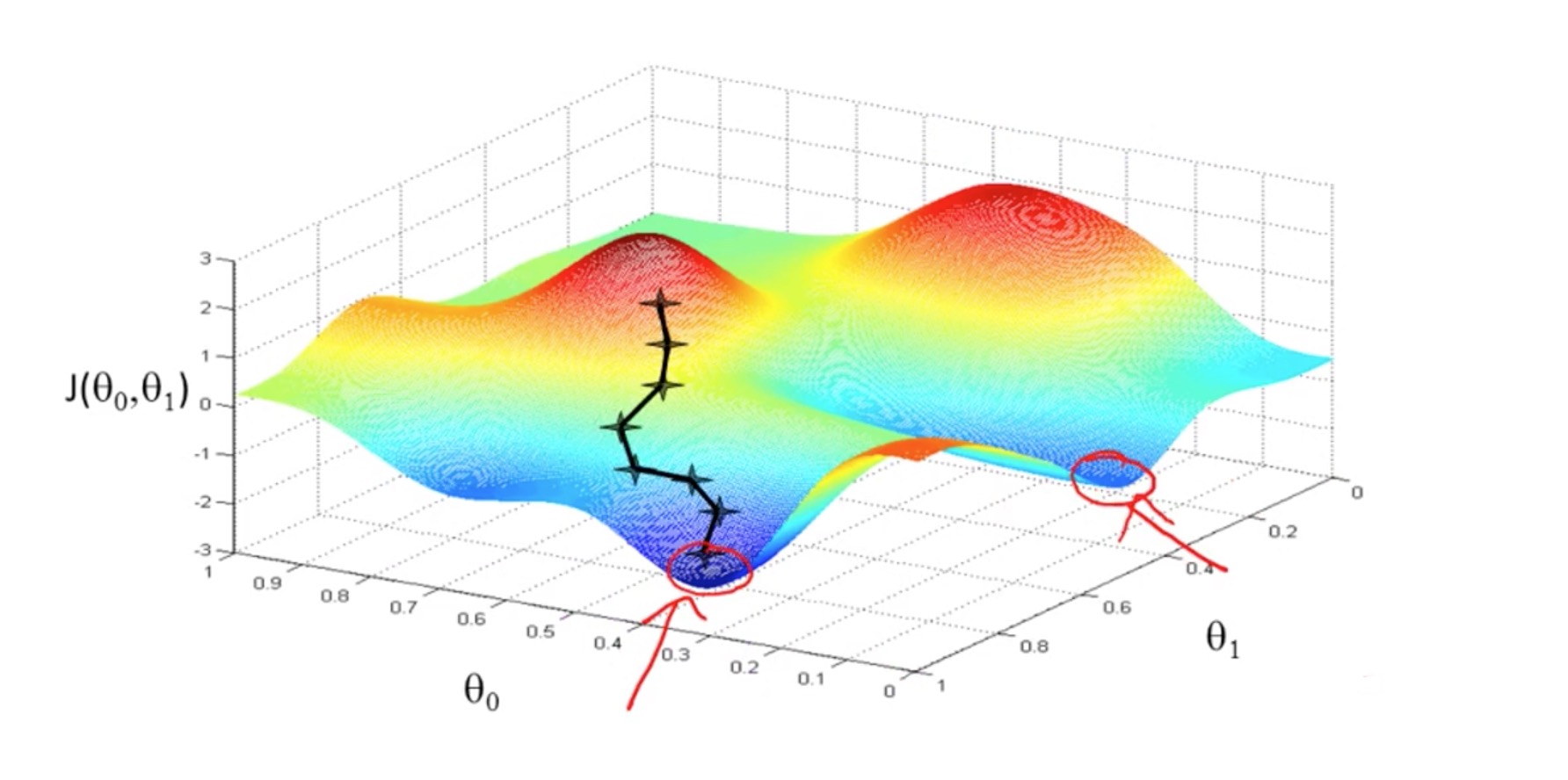
梯度上升代码演示

说完原理，在这里我要贴一下代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
import numpy as np
import math
def loadData():
    dataMat = []
    labelMat = []
    file = open('testSet.txt')
    for line in file.readlines():
        lineArr = line.strip().split()
        dataMat.append([1.0,float(lineArr[0]),float(lineArr[1])])
        labelMat.append(int(lineArr[2]))
    return dataMat,labelMat

def sigmoid(inX):
    inX = np.mat([math.exp(-a) for a in inX]).T
    return 1.0/(1 + inX)

def gradAscent(data,label):
    dataMat = np.mat(data)
    labelMat = np.mat(label).transpose()
    m,n = np.shape(dataMat)
    alpha = 0.001
    maxC = 500
    weights = np.ones((n,1))
    for k in range(maxC):
        h = sigmoid(dataMat * weights)
        error = (labelMat - h)
        weights = weights + alpha * dataMat.transpose() * error
    return weights

data,label = loadData()
print(gradAscent(data,label)) 
	# [[ 4.12414349]
		[ 0.48007329]
		[-0.6168482 ]]

关于上述代码可能存在一个异常，在这里你可以看一下我的博文，异常编号是 1 ：TypeError: only size-1 arrays can be converted to Python scalars

在运用 numpy 时出现的异常

我们绘制 testSet.txt 的图像如下：

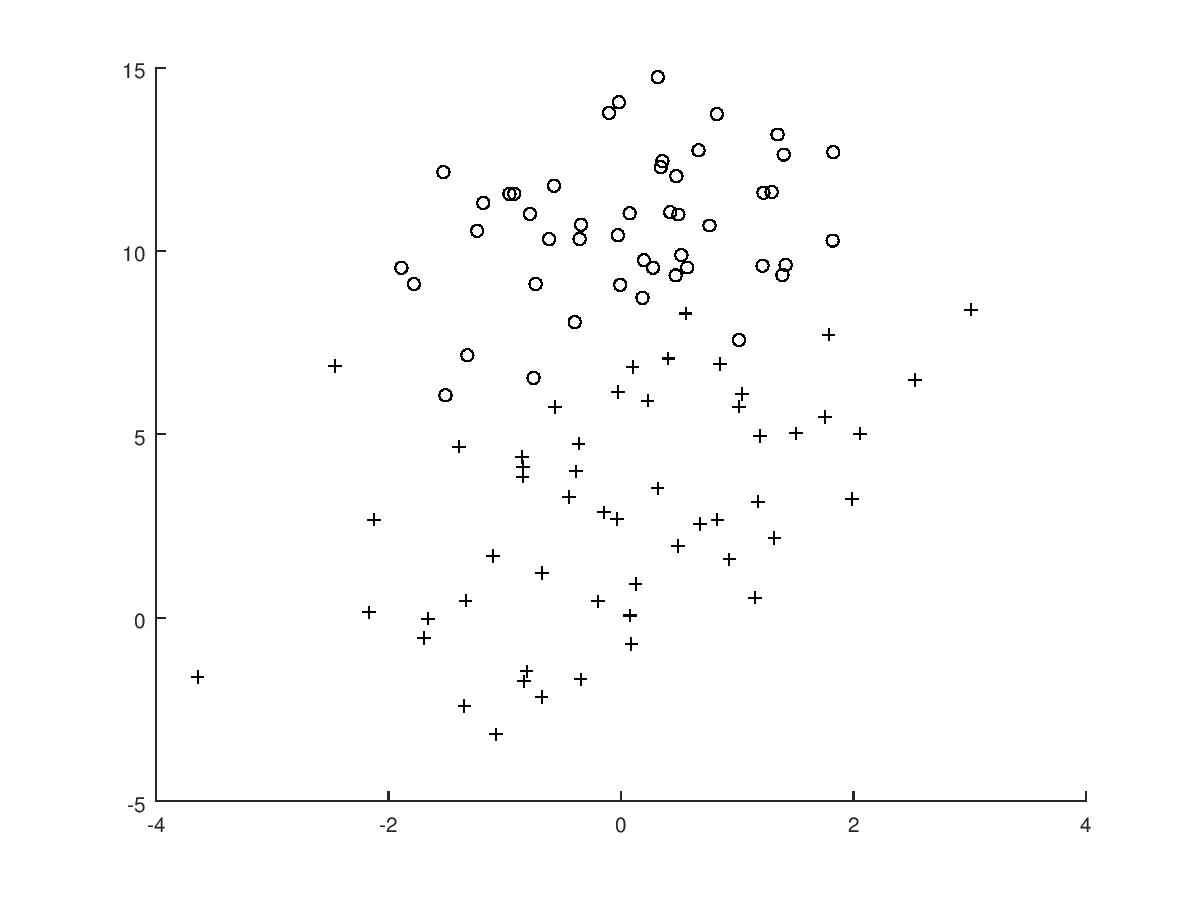
我们根据上面得到的 w 拟合直线，得：

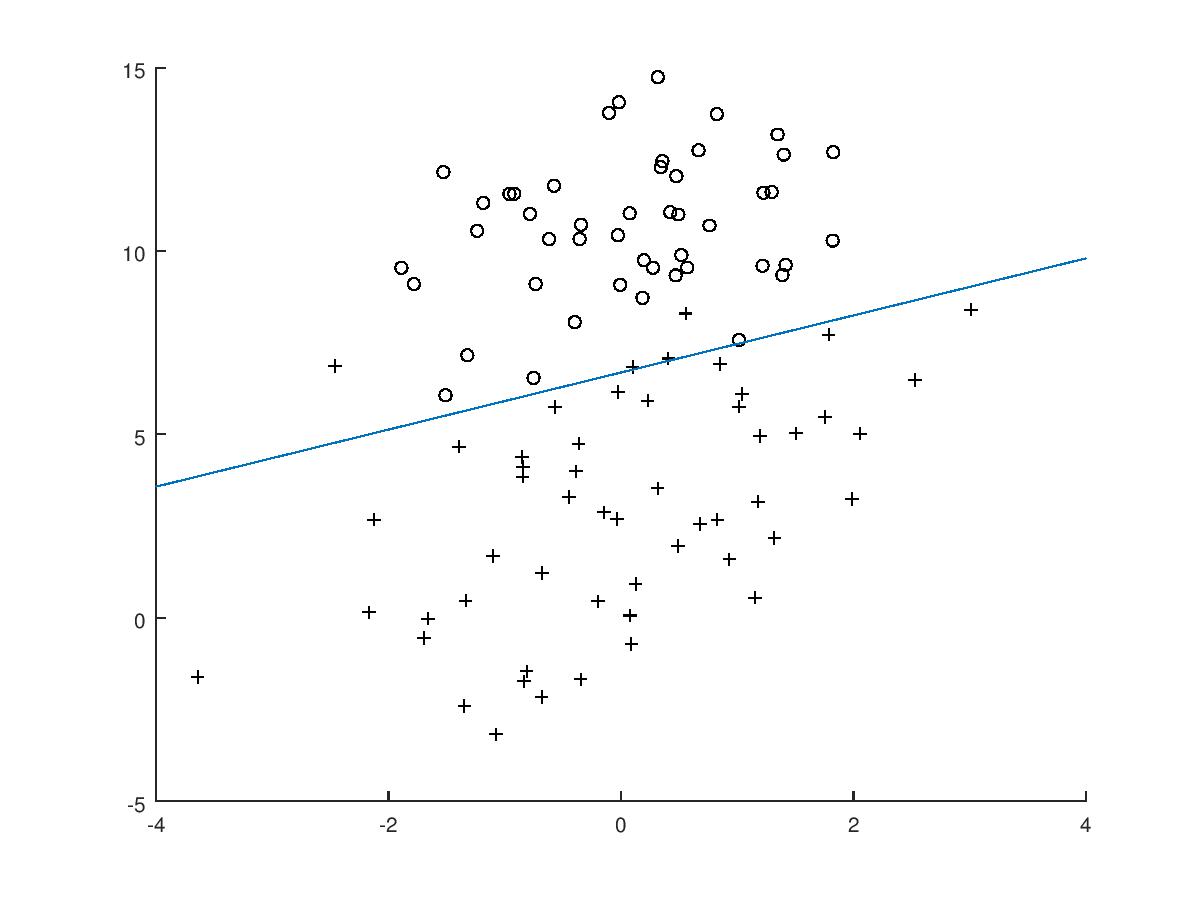
这里你可能有一个疑问，就是我们明明得到的是三个值，如何拟合一个二维数据。

看如下解释：

y = w0x0 + w1x1 + w2x2
因为 x0 等于 1 ，所以我们设 y = 0，我们的 x-y 的图像中，
x 是 x1 ，y 是 x2
所以只需要按下面式子求解即可
0 = w0 + w1x + w2y

随机梯度上升

其实我觉得随机梯度上升这个名字有点让人不可理解，如果改为逐步梯度上升我觉得会更好理解。

另外，这个随机二字是指上升的过程中具有随机性，而不是随机挑选数据。

我们看完梯度上升后，会发现最后拟合的非常好，但是有一点有点遗憾就是梯度上升的每一步都必须所有的数据参与(error)，如果数据量非常的大，那梯度上升不是一个好的算法。

所以我们选取单一样本进行梯度上升，一次仅用一个样本来更新回归系数。

看改进的如下代码：

1
最后的改进代码，运算起来不尽人意，所以暂时不贴了
请我喝杯咖啡吧～