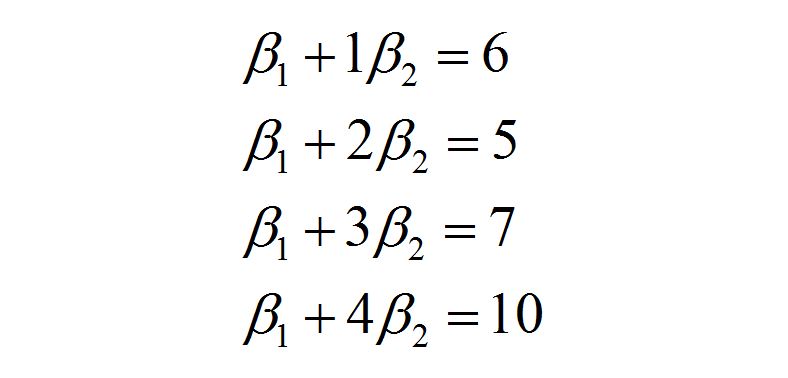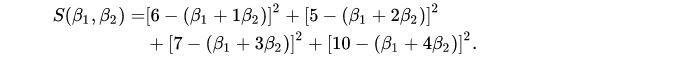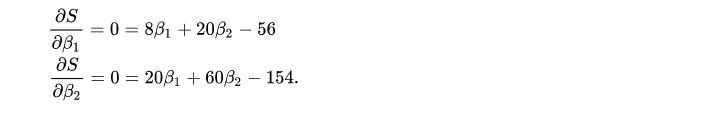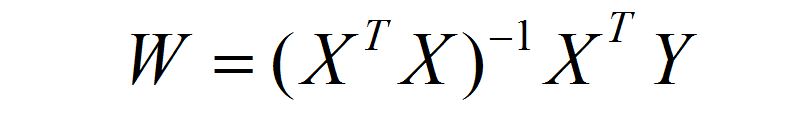资料来源:维基百科。
定义
最小二乘法(又称最小平方法)是一种数学优化技术。它通过最小化误差的平方和寻找数据的最佳函数匹配。
利用最小二乘法可以简便地求得未知的数据,并使得这些求得的数据与实际数据之间误差的平方和为最小。
最小二乘法是一种无偏算法。
例子
我们有以下数据
(1,6) (2,5) (3,7) (4,10)为了找出可以和这四点相匹配的直线,我们可以列式如下:
最小二乘法采用的手段是尽量使得等号两边的方差最小,也就是找出这个函数的最小值:
最小值可以通过对S(β1,β2)分别求 β1 和 β2 的偏导数,然后使它们等于零得到。
如此就得到了一个只有两个未知数的方程组,很容易就可以解出:
β1 = 3.5
β2 = 1.4也就是说直线 y = 3.5 + 1.4 * x 是最佳的。
但除了上述描述的梯度下降求之外,还有直接求的方法,看下面式子。
上面两种方法(梯度下降和直接求)都是最小二乘法。
关于上面式子的讲解,你可以参考的的博文。