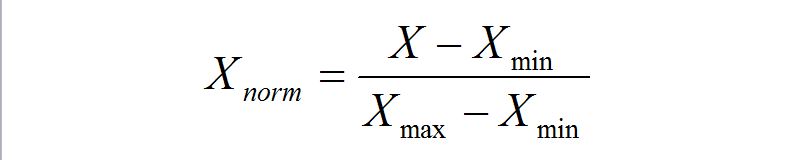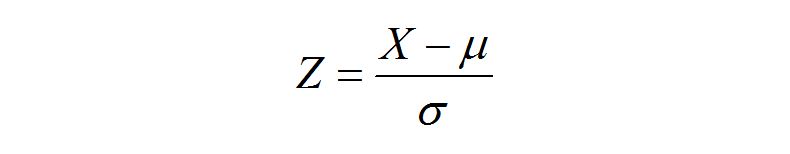归一化

把数变为（0，1）之间的小数，主要是为了数据处理方便提出来的，把数据映射到0～1范围之内处理，更加便捷快速。

min-max 标准化（线性函数归一化）

线性函数将原始数据线性化的方法转换到[0 1]的范围，归一化公式如下：

该方法实现对原始数据的等比例缩放，其中Xnorm为归一化后的数据，X为原始数据，Xmax、Xmin分别为原始数据集的最大值和最小值。

1
2
3

def Normalization(data):
    diff = np.max(data) - np.min(data)
    return (data - min) / diff

如果想讲数据映射到 [-1,1] 可以使用下面的公式

1
2
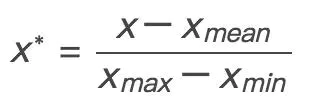
3

def Normalization(data):
    diff = np.max(data) - np.min(data)
    return (data - np.mean(data)) / diff

在不涉及距离度量、协方差计算、数据不符合正太分布的时候

数据的标准化是将数据按比例缩放，使之落入一个小的特定区间。由于信用指标体系的各个指标度量单位是不同的，为了能够将指标参与评价计算，需要对指标进行规范化处理，通过函数变换将其数值映射到某个数值区间。

又叫标准差归一化。

0均值归一化方法将原始数据集归一化为均值为0、方差1的数据集，归一化公式如下：

其中，

该种归一化方式要求原始数据的分布可以近似为高斯分布，否则归一化的效果会变得很糟糕。

def zero_standardize(data):
	mean = np.mean(data)
	stad = np.stad(data)
	return (data - mean) / stad

正态分布又名高斯分布，是一个非常常见的连续概率分布。
若随机变量X服从一个数学期望为μ、方差为σ^2的正态分布，记为N(μ，σ^2)。
其概率密度函数为正态分布的期望值μ决定了其位置，其标准差σ决定了分布的幅度。
当μ = 0,σ = 1时的正态分布是标准正态分布。

在分类、聚类算法中，需要使用距离来度量相似性的时候、或者使用PCA技术进行降维的时候。