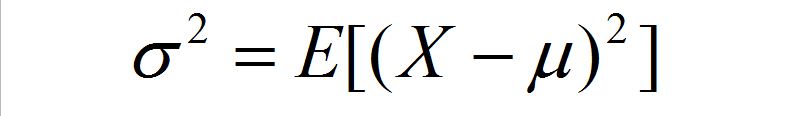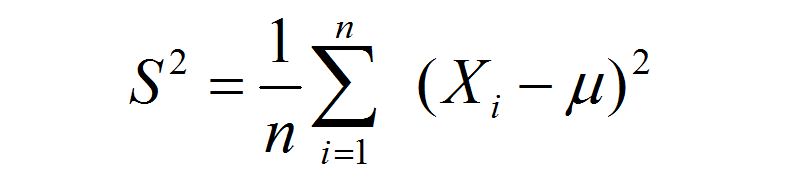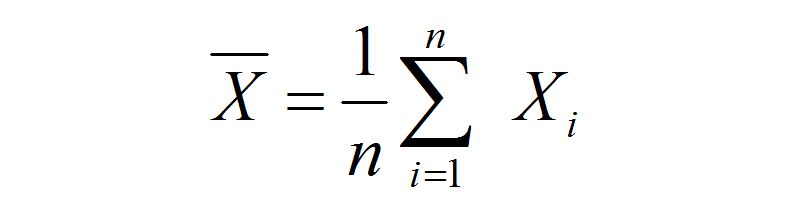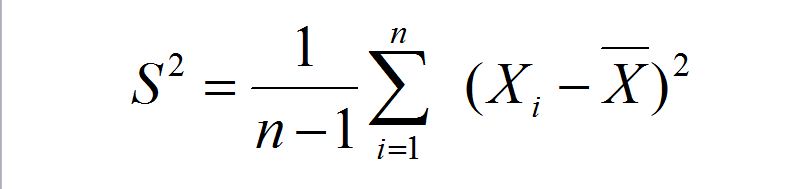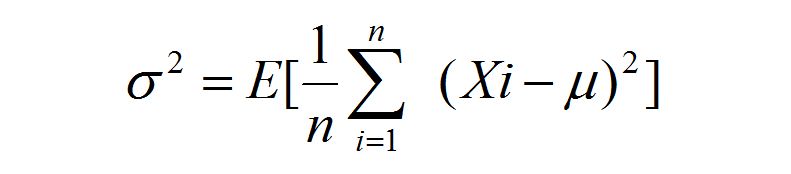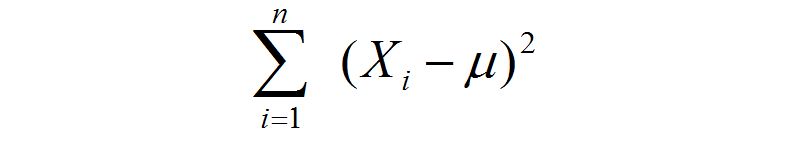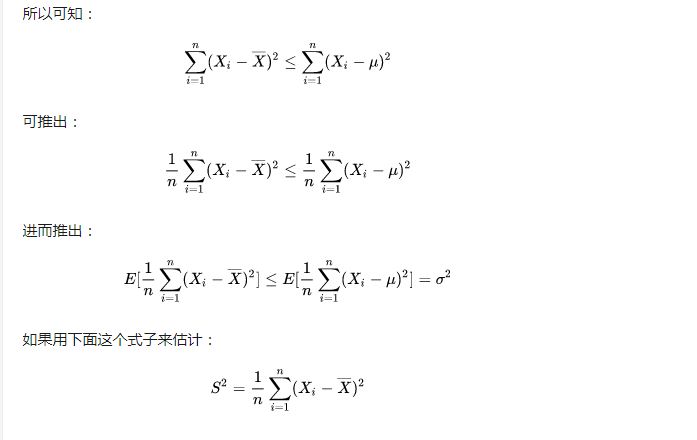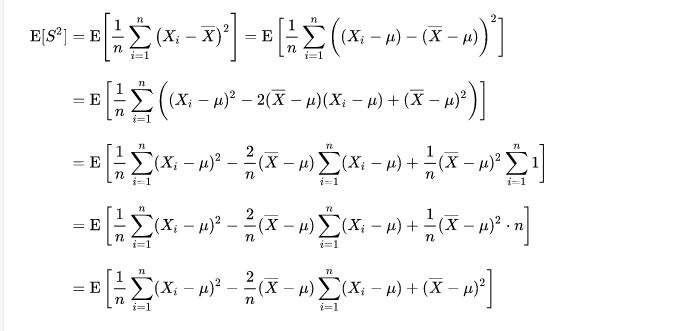为什么样本方差（sample variance）的分母是 n-1？

再次申明感谢逼乎。

看之前应该了解的知识

总体方差公式与求样本方差的公式差别是：总体方差是除以n，样本方差是除以(n-1)。

总体方差，样本方差

总体方差：

也叫做有偏估计，其实就是我们从初高中就学到的那个标准定义的方差，除数是N。如“果实现已知期望值，比如测水的沸点，那么测量10次，测量值和期望值之间是独立的（期望值不依测量值而改变，随你怎么折腾，温度计坏了也好，看反了也好，总之，期望值应该是100度），那么E『（X-期望）^2』，就有10个自由度。事实上，它等于（X-期望）的方差，减去（X-期望）的平方。” 所以叫做有偏估计，测量结果偏于那个”已知的期望值“。

样本方差：

无偏估计、无偏方差（unbiased variance）。对于一组随机变量，从中随机抽取N个样本，这组样本的方差就是Xi^2平方和除以N-1。这可以推导出来的。如果现在往水里撒把盐，水的沸点未知了，那我该怎么办？我只能以样本的平均值，来代替原先那个期望100度。同样的过程，但原先的（X-期望），被（X-均值）所代替。设想一下（Xi-均值）的方差，它不在等于Xi的方差，而是有一个协方差，因为均值中，有一项Xi/n是和Xi相关的，这就是那个”偏”的由来

OK,让我来浅显的解释一下，为什么总体方差是有偏，而样本方差是无偏。

首先，有偏的定义；

在统计学中，估计量的偏差（或偏差函数）是此估计量的期望值与估计参数的真值之差。偏差为零的估计量或决策规则称为无偏的。否则该估计量是有偏的。在统计中，“偏差”是一个函数的客观陈述。

先把问题完整地描述下。

如果已知随机变量 X 的期望为 μ ，那么可以如下计算方差 σ^2：

上面的式子需要知道 X 的具体分布是什么（在现实应用中往往不知道准确分布），计算起来也比较复杂。

所以实践中常常采样之后，用下面这个 S^2 来近似 σ ^2 ：

其实现实中，往往连 X 的期望 μ 也不清楚，只知道样本的均值：

那么可以这么来计算 S^2 ：

那这里就有两个问题了：

为什么可以用 S^2 来近似 σ ^2 ？

举个例子，假设 X 服从这么一个正态分布：

X ~ N(145,1.4^2)

即 μ = 145， σ ^2 = 1.96，图形如下：

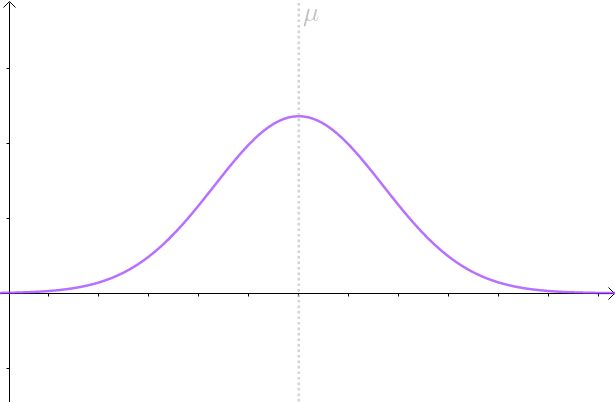
当然，现实中往往并不清楚 X 服从的分布是什么，具体参数又是什么？所以用虚线来表明我们并不是真正知道 X 的分布：

很幸运的，我们知道 μ =145 ，因此对 X 采样，并通过：

来估计 σ ^2 。某次采样计算出来的 S^2 ：

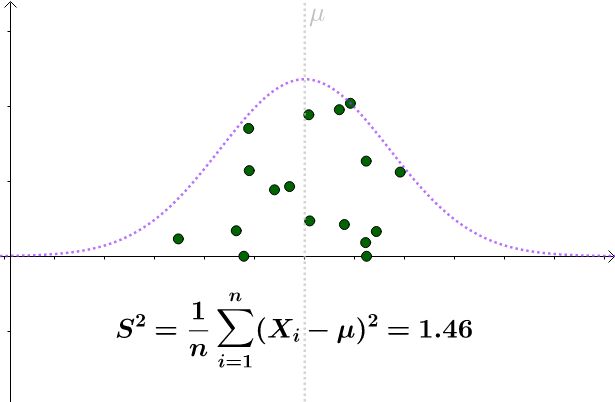
看起来比 σ ^2=1.96 要小。采样具有随机性，我们多采样几次， S^2 会围绕 σ ^2 上下波动：

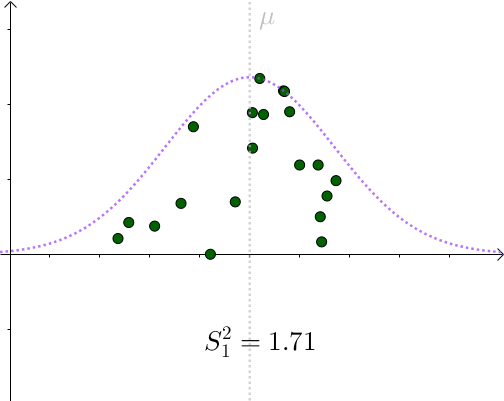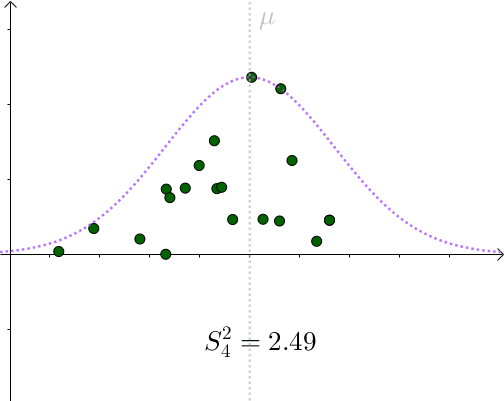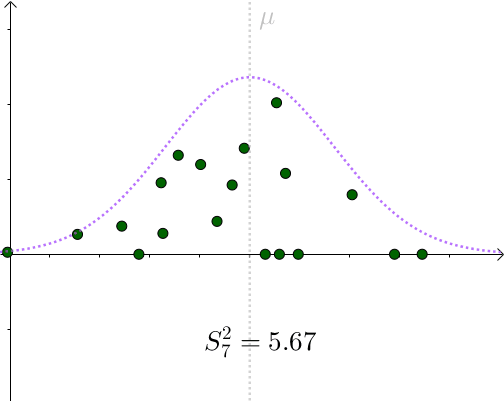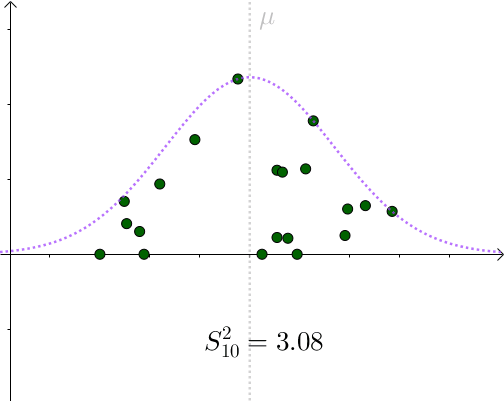
用 S^2 作为 σ ^2 的一个估计量，算是可以接受的选择。

很容易算出：

因此，根据中心极限定理， S^2 的采样均值会服从 μ =1.4^2 的正态分布：

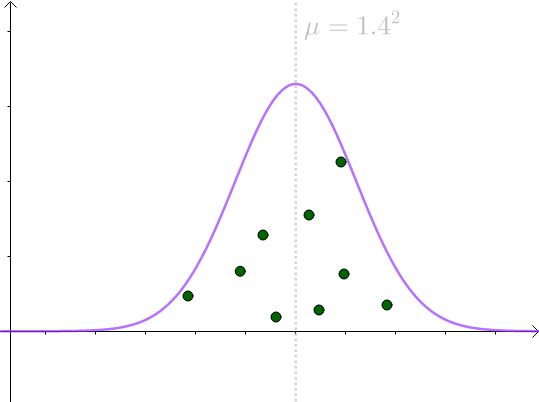
这也就是所谓的无偏估计量。从这个分布来看，选择 S^2 作为估计量确实可以接受。

为什么使用样本均值替代 μ 之后，分母是 1 / (n-1) ？

更多的情况，我们不知道 μ 是多少的，只能计算出样本均值。不同的采样对应不同的样本均值：

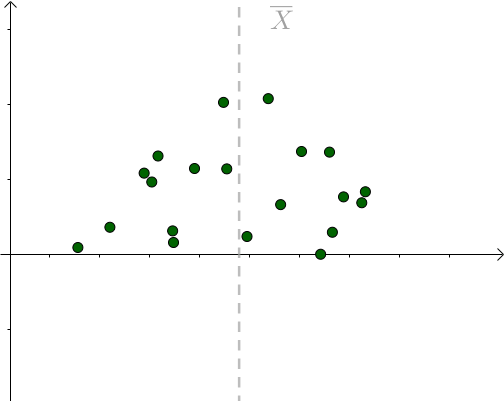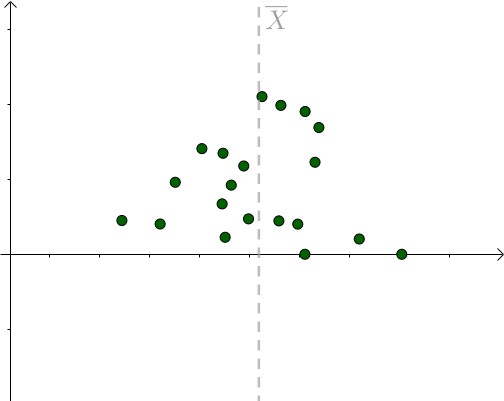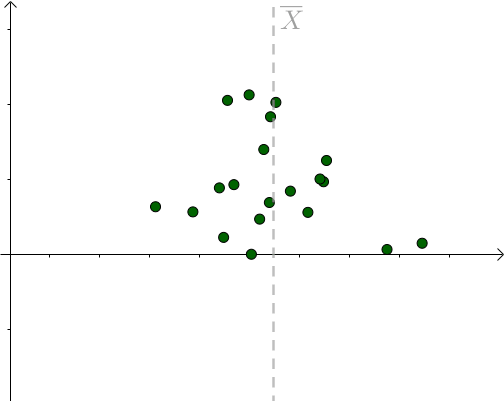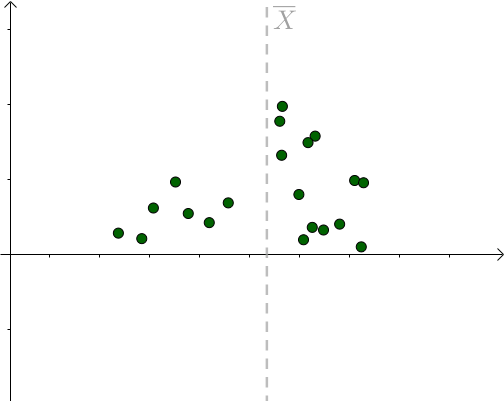
对于某次采样而言，当 μ = 样本均值时，下式取得最小值：

我们也是比较容易从图像中观察出这一点，只要 μ 偏离样本均值，该值就会增大：

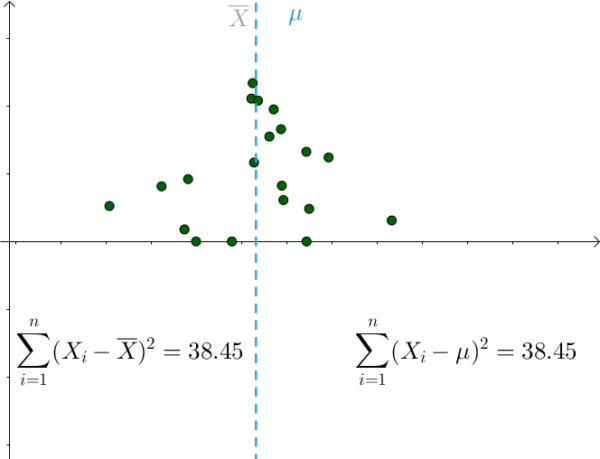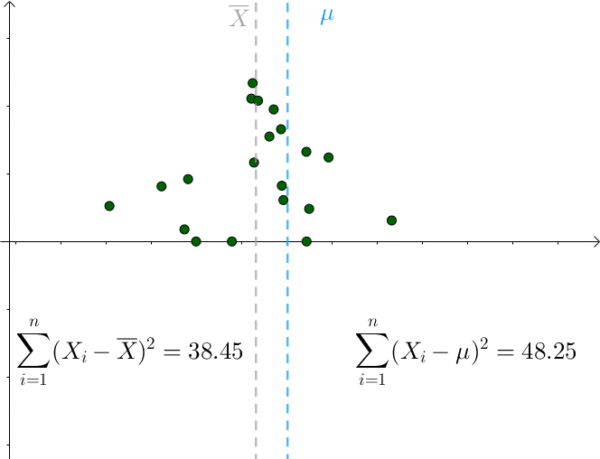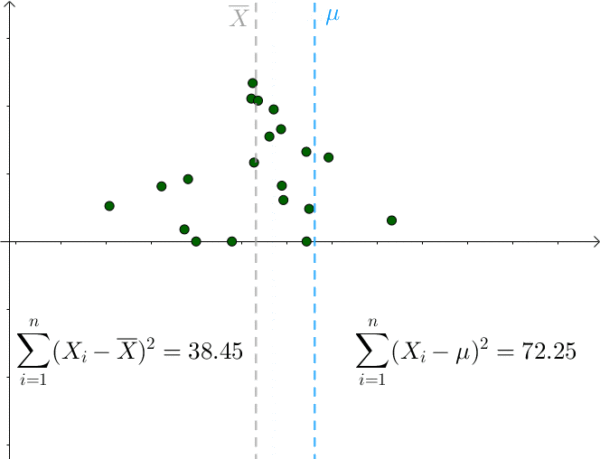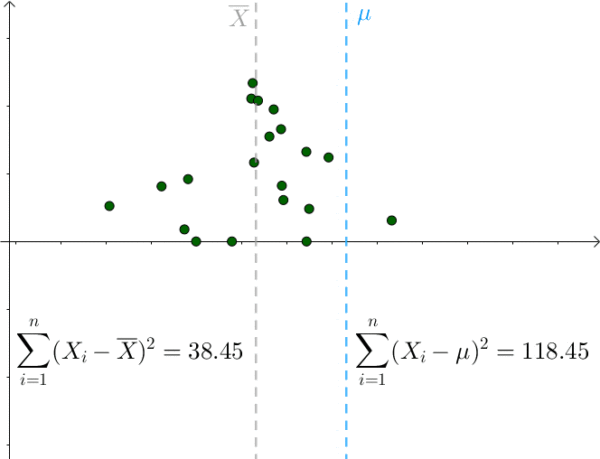
那么 S^2 采样均值会服从一个偏离 1.4^2 的正态分布：

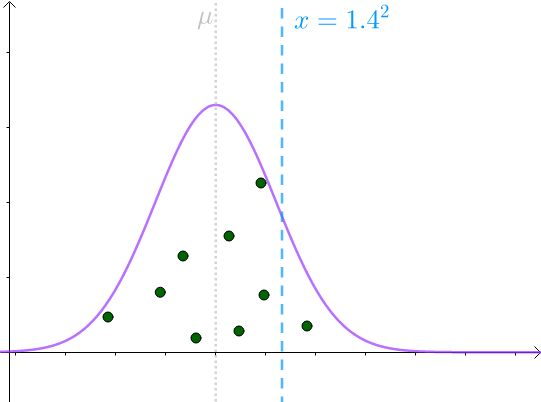
可见，此分布倾向于低估 σ ^2 。

具体小了多少，我们可以来算下：

另一个比较精炼的回答

作者：魏天闻

链接

样本方差计算公式里分母为的目的是为了让方差的估计是无偏的。无偏的估计(unbiased estimator)比有偏估计(biased estimator)更好是符合直觉的，尽管有的统计学家认为让mean square error即MSE最小才更有意义，这个问题我们不在这里探讨；不符合直觉的是，为什么分母必须得是而不是才能使得该估计无偏。我相信这是题主真正困惑的地方。要回答这个问题，偷懒的办法是让困惑的题主去看下面这个等式的数学证明：