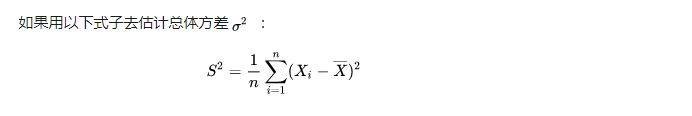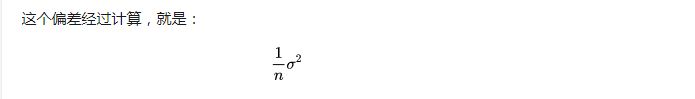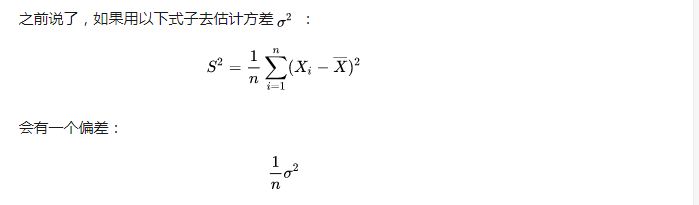这个问题可能困扰大家很久,所以在查阅资料后,在此记录。
感谢逼乎里面人的讲解。
什么是无偏估计?
答案一:
作者:TomHall
比如我要对某个学校一个年级的上千个学生估计他们的平均水平(真实值,上帝才知道的数字),那么我决定抽样来计算。
我抽出一个10个人的样本,可以计算出一个均值。
那么如果我下次重新抽样,抽到的10个人可能就不一样了,那么这个从样本里面计算出来的均值可能就变了,对不对?
因为这个均值是随着我抽样变化的,而我抽出哪10个人来计算这个数字是随机的,那么这个均值也是随机的。
但是这个均值也会服从一个规律(一个分布),那就是如果我抽很多次样本,计算出很多个这样的均值,这么多均值们的平均数应该接近上帝才知道的真实平均水平。
如果你能理解“样本均值”其实也是一个随机变量,那么就可以理解为这个随机变量的期望是真实值,所以无偏(这是无偏的定义);而它又是一个随机变量,只是估计而不精确地等于,所以是无偏估计量。答案二:
作者:包龙图
给你举个例子吧:
现在甲市有一万名小学三年级学生,他们进行了一次统考,考试成绩服从1~100的均匀分布:
00001号学生得1分,00002号学生得1.01分……10000号学生得100分。那么他们的平均分是多少?
(1+1.01+1.02+....+100)/10000=50.5,这个值叫做总体平均数。
现在假定你是教委的一个基层人员,教委主任给你一个早上时间,让你估算一下全市学生的平均成绩,你怎么办?
把全市一万名学生都问一遍再计算时间显然是来不及了,因此在有限的时间里,你找到了一个聪明的办法:
给全市的78所小学每一所学校打了一个电话,让他们随机选取一名学生的成绩报上来,这样你就得到了78个学生的成绩,这78个学生就是你的样本。
你现在的任务很简单了,拿这78个学生的成绩相加并除以78,你就得到了样本平均数。
你把这个数报告给教委主任,这个数就是你估算出来的全市平均成绩。这个样本平均数会不会等于总体平均数50.5?
很显然这和你的“手气”有关——不过大多数情况下是不会相等的。
那么问题来了:既然样本平均数不等于总体平均数(也就是说你报给教委主任的平均分和实际的平均分非常有可能是不一样的),要它还有用吗?
有!因为样本平均数是总体平均数的无偏估计——也就是说只要你采用这种方法进行估算,估算的结果的期望值(你可以近似理解为很多次估算结果的平均数)既不会大于真实的平均数,也不会小于之。
换句话说:你这种估算方法没有系统上的偏差,而产生误差的原因只有一个:随机因素(也就是你的手气好坏造成的)。关于有偏和无偏
这是知乎马同学的原创。
现实中常常有这样的问题,比如,想知道全体女性的身高均值 μ ,但是没有办法把每个女性都进行测量,只有抽样一些女性来估计全体女性的身高:
那么根据抽样数据怎么进行推断?什么样的推断方法可以称为“好”?
1 无偏性
比如说我们采样到的女性身高分别为:
{x1,x2,x3...}那么:
是对 μ 不错的一个估计,为什么?因为它是无偏估计。
首先,真正的全体女性的身高均值 ,我们是不知道,只有上帝才知道,在图中就画为虚线:

我们通过采样计算出样本平均值:
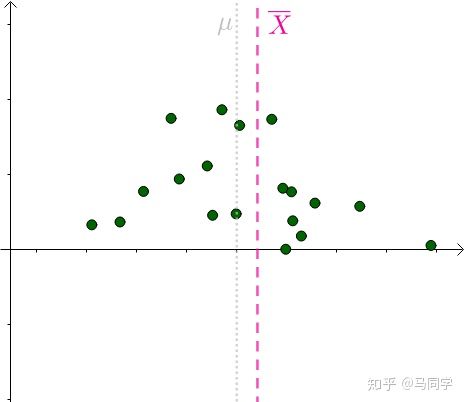
会发现,不同采样得到的样本平均值 是围绕 μ 左右波动的:

这有点像打靶,只要命中在靶心周围,还算不错的成绩,这就是无偏的:

根据
为什么样本方差(sample variance)的分母是 n-1?
解释,会偏离靶心、产生偏差,这就是有偏的:
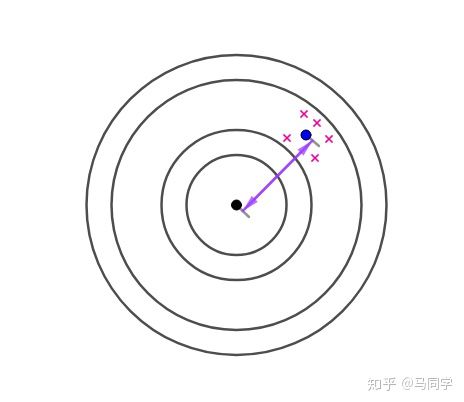
这种偏差就好像瞄准镜歪了,是系统性的:

就此而言,无偏估计要好于有偏估计。
2 有效性
打靶的时候,右边的成绩肯定更优秀:

进行估计的时候也是,估计量越靠近目标,效果越“好”。这个“靠近”可以用方差来衡量。
比如,仍然对 μ 进行估计,方差越小,估计量的分布越接近 μ :
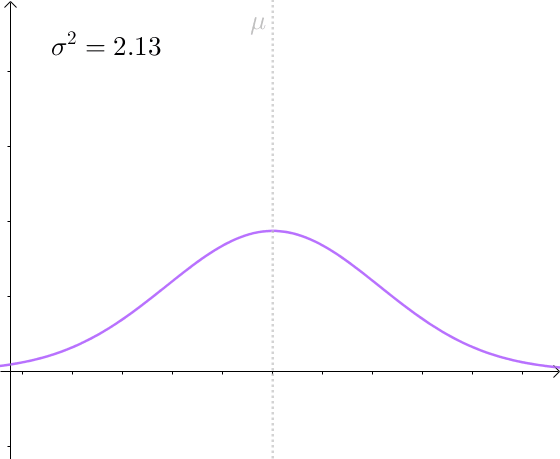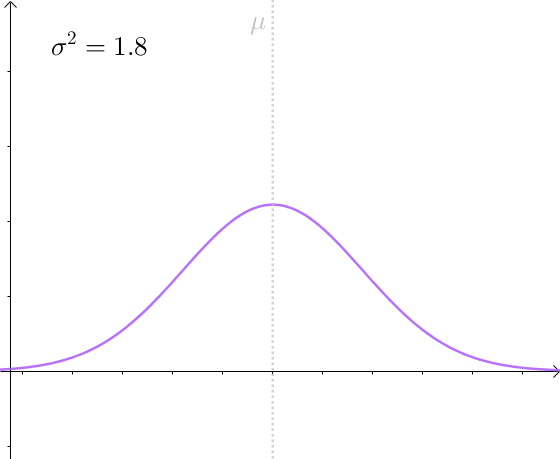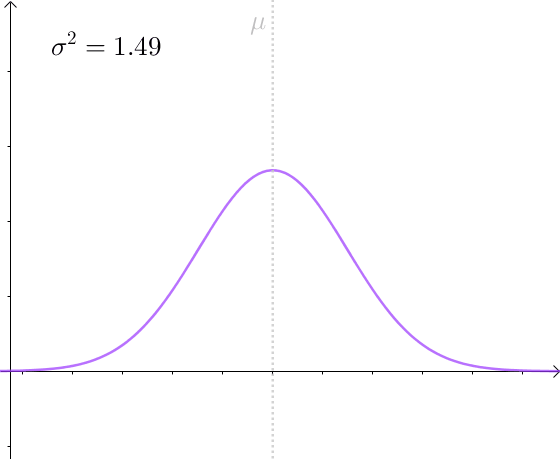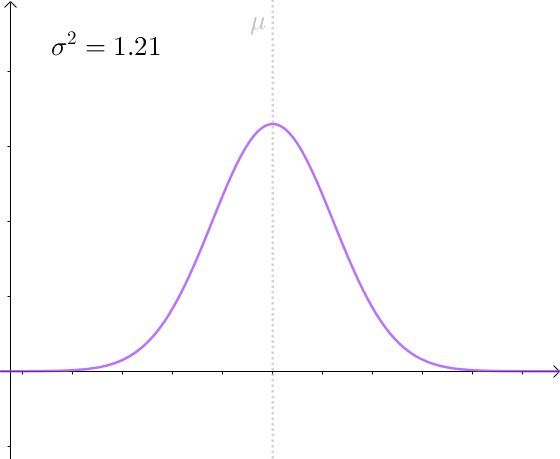
有效估计和无偏估计是不相关的:
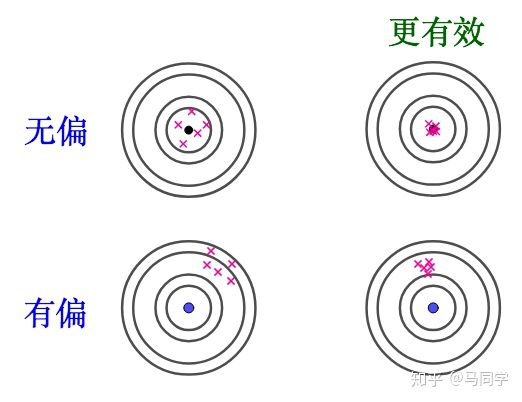
但是后者比前者方差小,后者更有效。
并且在现实中不一定非要选无偏估计量,比如:
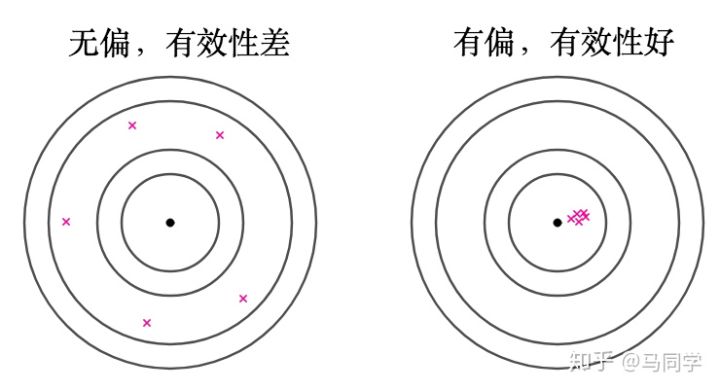
如果能接受点误差,我倒觉得选择右边这个估计量更好。
3 一致性
可以看到,随着采样个数n 的增加,这个偏差会越来越小。那么这个估计就是“一致”的。
如果样本数够多,其实这种“有偏”但是“一致”的估计量也是可以选的。
4 总结
判断一个估计量“好坏”,至少可以从以下三个方面来考虑:
无偏
有效
一致
实际操作中,要找到满足三个方面的量有时候并不容易,可以根据情况进行取舍。