决策树

决策树是常见的机器学习分类算法。

这里讲述的是 ID3 算法。

github

它的原理很简单，比如有如下数据：判断是否是鱼，我们有特征在水中生活，有鳞。可以画出决策树图：

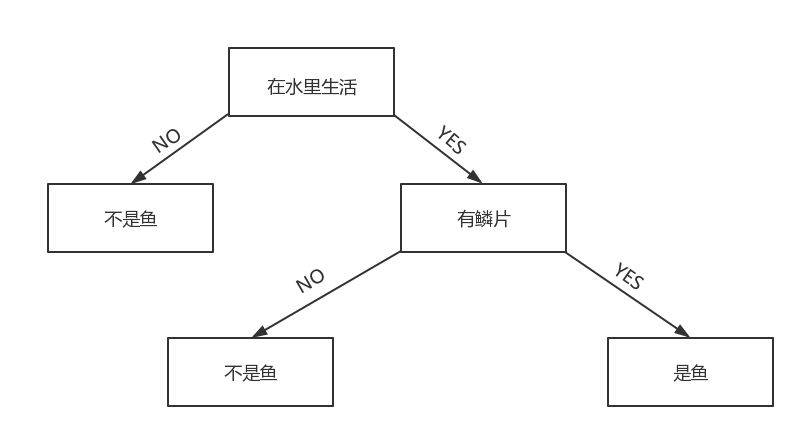
根据这幅图，我们就可以收集数据，然后在根据特征来判断是否是鱼。

但是，这里有一个问题，我们如何确认第一个判断标准是在水中生活，还有有鳞呢？

如果判断的第一个标准是有鳞，那么在 分支 no 上也可能会出现有鱼的分支，所以分支数的增加，会导致算法越来越复杂，效率下降。

所以，我们引入信息熵来判断，如何选取判断标准。

信息熵

关于信息熵，我的一个文章已经很好的介绍过了。

信息熵到底是什么

但是，在这里我还是要简单的介绍下里面的注意点。

划分选择

我们还是举例子：

信息熵的定义：

Ent(D) = -∑ p * log(p,2)

信息增益：

Gain(D,a) = Ent(D) - ∑ (|Dv| / |D| ) * Ent(Dv)

其中 Ent(D) 为该分支节点的信息熵 Ent(Dv) 代表的是某一属性的信息熵 |Dv| / |D| 代表这一属性值占样本总数的比例。

上述的三个描述很复杂，我也觉得充满不可理解的地方，所以还是直接看例子有助于消化。

一般而言，信息增益越大，就意味着用该属性来划分所得的“纯度提升” 越大。

如一共拥有17个训练数据，二分类问题（是否为鱼），其中不是鱼为 8 例，是鱼为 9 例。

所以正例 P1 = 9 / 17 反例 P2 = 8 / 17

计算二维信息熵

Ent(D) = -(8/17 * log(8/17,2) + 9/17 * log(9/17,2)) = 0.998

在计算各个特征的信息增益：

假设在是否水生中 是占10例 不是占 7例，则：

而在 是水生 的例子中，是鱼占 5 例，不是鱼占 5 例：

所以信息熵为：

Ent(D1) = -(5/10 * log(5/10,2) + 5/10 * log(5/10,2)) = 0.500

在 不是水生 的例子中，是鱼占 0 例，不是鱼占 7 例，

计算信息熵为：

Ent(D2) = -(7/7 * log(7/7,2)) = 0.000

计算水生的信息增益：

Gain(D,是否水生) = Ent(D) - (Ent(D1) * 10/17 + Ent(D2) * 7/17) = 0.198

我们在计算其它特征的信息增益，如是否为有鳞，计算得：

Gain(D,是否有鳞) = 0.720

这时候我们发现 Gain(D,是否水生) > Gain(D，是否有鳞)，所以，我们选用是否水生作为第一个判断标准。

PS：上面的计算值都是我乱编的，你要知道我们的目的不是计算数值，而是阐述思想。

复杂例子的信息增益的计算

我们再来考虑一个复杂一点的例子。

假设有如下数据，判断西瓜是否为好瓜的二分类问题。我们一共有 17 个训练数据，其中正例 8 个 ，反例 9 个。

计算初始信息熵：

Ent(D) = -(8/17 * log(8/17,2) + 9/17 * log(9/17 ,2)) = 0.998

计算色泽的信息增益：

比如 色泽 = （青绿，乌黑，浅白），设这个属性代号为 C

对于青绿我们一共有 6 个样例。其中 3 个反例，3 个正例。

Ent(C,青绿) = -(3/6 * log(3/6,2) + 3/6 * log(3/6,2)) = 1.000

对于乌黑我们一共有 6 个样例，其中 4 个正例，2 个反例

Ent(C,乌黑) = -(4/6 * log(4/6,2) + 2/6 * log(2/6,2)) = 0.918

对于浅白我们一共有 5 个样例，其中 1 个正例，4 个反例

Ent(C,浅白) = -(1/5 * log(1/5,2) + 4/5 * log(4/5,2)) = 0.722

计算色泽的信息增益：

Gain(D,色泽) = Ent(D) - ∑ (|Dv| / |D| ) * Ent(Dv)

即

Gain(D,色泽) = 0.998 - (6/17 * 1.000 + 6/17 * 0.918 + 5/17 * 0.722) = 0.109

我们在计算其它特征，比如纹理，敲声的等信息增益，选取最大的那个作为判断标准，如果同时存在多个最大增益，则可以任意选取一个。

对于信息增益的注意点

事实上，我们的每一次划分都会将一个属性减去，然后在这个属性上再次划分分支，比如我们上面判断西瓜是好坏，假设我们判断的根节点是色泽。如图所示：

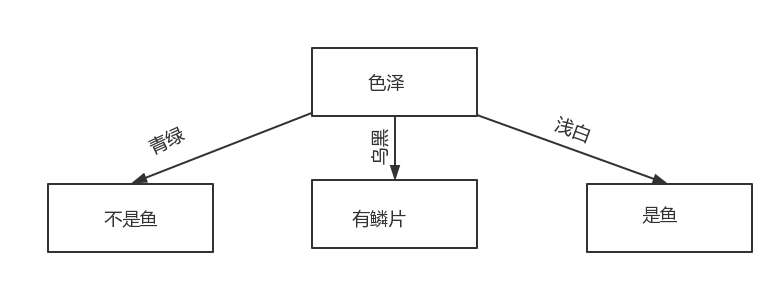
我们发现上面已经分成了 3 个分支。

而，在上面的例子我们可以知道，以青绿为例，青绿的例子一共有 6 个，其中 3 个正例，3 个反例。

因为现在的样例合集变成了青绿合集，所以，我们的信息熵也要相应的变成青绿信息熵，而不是原来的信息熵。

即，信息熵为

Ent(青绿) = - (3/6 * log(3/6,2) + 3/6 * log(3/6,2)) = 1.000

然后我们在根据青绿旗下的其他属性，计算各自的信息增益，然后有信息增益继续划分分支。

在这里，我们可以很清晰的得到，分支就完全各自为政了，所以，各自分支下判断标准也可能不一样。如青绿下的判断标准是纹理，而乌黑下的判断标准是敲声。

代码示例

创建数据

def createData():
    dataSet = [

        [1,1,'yes'],
        [1,1,'yes'],
        [1,0,'no'],
        [0,1,'no'],
        [0,1,'no']
    ]
    labels = ['no surfacing','flippers']
    return dataSet,labels

计算信息熵

def calcShannon(dataSet): #计算香农熵（信息熵）
    num     = len(dataSet)
    labels  = {}
    for feat in dataSet:
        currentLabel = feat[-1] #得到标签
        if currentLabel not in labels.keys():
            labels[currentLabel] = 0
        labels[currentLabel] += 1
    shannon = 0.0
    for key in labels:
        prob     = float(labels[key]) / num
        shannon -= prob * (math.log(prob,2))
    return shannon

分割数据

其目的是比如西瓜的色泽属性，将色泽为青绿的分为一个数据集，乌黑的分为另一个数据集，浅白的分为其他数据集

def spiltData(dataset,axis,value): #将同一属性的同一数值划分到同一数据集
   retData = []
   for feat in dataset:
       if feat[axis] == value:
           redData   = feat[:axis]
           redData.extend(feat[axis + 1:])
           retData.append(redData)
   return retData

选取最大的信息增益

我们有公式：

信息增益：

Gain(D,a) = Ent(D) - ∑ (|Dv| / |D| ) * Ent(Dv)

def chooseBest(dataSet):
    num        = len(dataSet[0]) - 1  #得到除了标签之外的属性长度
    base       = calcShannon(dataSet) #计算原始信息熵
    bestGain   = 0.0                  #初始化最好的信息熵
    bestFeature = -1                  #初始化最好的信息熵为哪个属性的坐标
    for i in range(num):
        featList   = [example[i] for example in dataSet]  # 将相同属性的值转化为同一列表，即将一列的属性转到同一个列表中
        uniVals    = set(featList)                        # set 将去掉相同的数值 set(1,2,1,4,3,2) = 1,2,3,4
        newShannon = 0.0                                  #初始化每一个属性的香农熵
        # 关于下面一开始我有一个不理解的地方，就是感觉将其同一属性分为不同的数据集计算信息熵有点多余
        # 不如，一开始就用同一属性的全部数据集计算信息熵
        # 其实，上述是对信息熵的不完全理解导致的
        # 信息熵是 p * log(p,2) 而 p 正是同一属性中同一值所占据的比例
        # 如果没有划分不同的数据集的话就无法计算这个比例
        for value in uniVals:
            subDataSet  = spiltData(dataSet,i,value)             #对于同一属性按照相同值划分数据集，比如对于属性大小 很大为一个数据集 不大为另一个数据集
            prob        = len(subDataSet) / float(len(dataSet))  #得到同一数据集占同一属性数据集的比例
            newShannon += prob * calcShannon(subDataSet)                #计算同一值的数据集的信息熵
        infoGain = base - newShannon                      #这是因为信息熵本来前面就有 负号，而上面是加号所以这边填上负号
        if(infoGain > bestGain):
            bestGain    = infoGain
            bestFeature = i
    return bestFeature

返回出现次数最多的分类名称

选择出现次数最高的标签，如[1,2,1,1] 就返回 1

def major(classList):                       #
    classCount = {}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote]  = 0
        classCount[vote] += 1
    sortClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse=True)
    return sortClassCount[0][0]

构建决策树

关于下面递归的使用，你可以详细的参考我的另一篇文章。

递归

def createTree(dataSet,labels):
   classList = [example[-1] for example in dataSet]    #得到标签
   if classList.count(classList[0]) == len(classList): #
       return classList[0]
   if len(dataSet[0]) == 1:                            #如果所有的标签都变遍历完了，就说明所有的都已经 tree 创建好了
       return major(classList)
   bestFeat = chooseBest(dataSet)  #得到最佳信息熵的下标
   bestFeatLabel = labels[bestFeat] #得到最佳信息熵的标志
   myTree = {bestFeatLabel:{}}      #初始化 tree 并且将最佳标志加上
   del(labels[bestFeat])            #删除标签上的最佳标志
   featVal = [example[bestFeat] for example in dataSet] #将最佳属性的值放在 featVal
   uniVals = set(featVal)
   for value in uniVals:
       subLabels = labels[:]        #复制已经去除最佳标签的数组
       myTree[bestFeatLabel][value] = createTree(spiltData(dataSet,bestFeat,value),subLabels) #对分支标签加上属性值
   return myTree

运行

data,labels= createData()
myTree = createTree(data,labels)
print(myTree)

结果

{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}