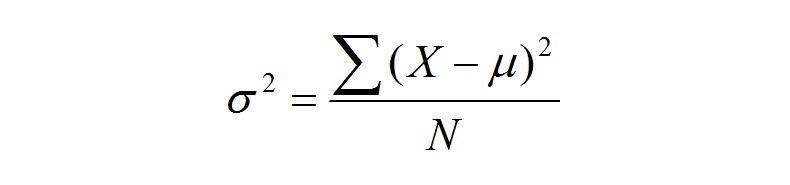姑苏城外一茅屋，万树梅花月满天

0%

python-numpy-函数详解

发表于 更新于 分类于 ， ， ， Valine：

Here is the tutorial of python’s numpy.

基础函数

np.ones: 创建一个数组, 其中的元素全为 1

np.zeros: 创建元素全为 0 的数组, 类似 np.ones

np.empty创建一个内容随机并且依赖与内存状态的数组。

np.eye: 创建一个对角线为 1 其他为 0 的矩阵.

np.identity: 创建一个主对角线为 1 其他为 0 的方阵.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
np.zeros((3,4))
	# [[ 0.  0.  0.  0.]
		[ 0.  0.  0.  0.]
		[ 0.  0.  0.  0.]]

np.ones((3,4))
	# [[ 1.  1.  1.  1.]
		[ 1.  1.  1.  1.]
		[ 1.  1.  1.  1.]]

np.eye(3)
	# [[ 1.  0.  0.]
		[ 0.  1.  0.]
	[ 0.  0.  1.]]

A

asarray

array和asarray都可以将结构数据转化为ndarray，但是主要区别就是当数据源是ndarray时，array仍然会copy出一个副本，占用新的内存，但asarray不会。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
data1 = [[1, 1, 1], [1, 1, 1], [1, 1, 1]]
arr2 = np.array(data1)
arr3 = np.asarray(data1)
data1[1][1] = 2
print('data1:\n', data1)
print('arr2:\n', arr2)
print('arr3:\n', arr3)

	data1:
	 [[1, 1, 1], [1, 2, 1], [1, 1, 1]]
	arr2:
	 [[1 1 1]
	 [1 1 1]
	 [1 1 1]]
	arr3:
	 [[1 1 1]
	 [1 1 1]
	 [1 1 1]]

如果数据源是 narray

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
data1 = np.array([[1, 1, 1], [1, 1, 1], [1, 1, 1]])
arr2 = np.array(data1)
arr3 = np.asarray(data1)
data1[1][1] = 2
print('data1:\n', data1)
print('arr2:\n', arr2)
print('arr3:\n', arr3)

	data1:
	 [[1 1 1]
	 [1 2 1]
	 [1 1 1]]
	arr2:
	 [[1 1 1]
	 [1 1 1]
	 [1 1 1]]
	arr3:
	 [[1 1 1]
	 [1 2 1]
	 [1 1 1]]

python numpy array 函数用法

使用numpy.array方法将tuple和list, array, 或者其他的序列模式的数据转创建为 ndarray, 默认创建一个新的 ndarray.

1
2
3
4
5
6
np.array([1,2,3,4]) 
	# [1 2 3 4]
 b = array( [ (1.5,2,3), 
                 (4,5,6)  ]  )　　 
	# array([[ 1.5,  2. ,  3. ],  
　　　  	[ 4. ,  5. ,  6. ]])

python numpy arange 函数用法

arange([start,] stop[, step,], dtype=None)根据start与stop指定的范围以及step设定的步长，生成一个 ndarray。

生成均匀分布的array。最后返回的如果不加处理一般是向量。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
np.arange(3)
	# array([0, 1, 2])
np.arange(3)[::-1]
	# [2,1,0]
np.arange(3.0)
	# array([ 0.,  1.,  2.])
np.arange(3,7)
	# array([3, 4, 5, 6])
np.arange(3,7,2)
	# array([3, 5])
 b = arange(12).reshape(4,3)  
	# [[ 0  1  2]  
		[ 3  4  5]  
		[ 6  7  8]  
		[ 9 10 11]]

python numpy argsort函数用法

argsort()函数返回的是数组从小到大值所对应的索引。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
import numpy as np
data = np.array([[3,2,5]]);
print(np.argsort(data));
	#[[1 0 2]]
#矩阵按照列排列（对象是单列）
data = np.array([[1,2],[2,3],[1,5]]);
print(np.argsort(data,axis=0));
	#[[0 0]
	#[2 1]
	#[1 2]]
矩阵按照行排列（对象是单行）
data = np.array([[1,2],[2,3],[1,5]]);
print(np.argsort(data,axis=1));
	#[[0 1]
	#[0 1]
	#[0 1]]

numpy argmax 函数

numpy.argmax(a, axis=None, out=None) 返回沿轴axis最大值的索引。

axis : int, 可选 默认情况下，索引的是平铺的数组，否则沿指定的轴。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
a = np.arange(6).reshape(2,3)
a
	#array([[0, 1, 2],
		[3, 4, 5]])
np.argmax(a)
	# 5
np.argmax(a, axis=0)#0代表列
	# array([1, 1, 1])
np.argmax(a, axis=1)#1代表行
	# array([2, 2])

b = np.arange(6)
b[1] = 5
b
	# array([0, 5, 2, 3, 4, 5])
np.argmax(b) # 只返回第一次出现的最大值的索引
	# 1

python numpy astype 函数

Numpy数据类型转换astype，dtype

1
2
3
4
5
6
7
8
9
10
arr = np.array([1,2,3,4,5])
arr
	array([1, 2, 3, 4, 5])
// 该命令查看数据类型
arr.dtype
	dtype('int64')
float_arr = arr.astype(np.float64)
// 该命令查看数据类型
float_arr.dtype
	dtype('float64')

转换数据类型

1
2
3
4
5
6
7
8
9
10
// 如果将浮点数转换为整数，则小数部分会被截断
arr2 = np.array([1.1, 2.2, 3.3, 4.4, 5.3221])
arr2
	array([ 1.1   ,  2.2   ,  3.3   ,  4.4   ,  5.3221])
// 查看当前数据类型
arr2.dtype
	dtype('float64')
// 转换数据类型  float -> int
arr2.astype(np.int32)
	array([1, 2, 3, 4, 5], dtype=int32)

字符串数组转换为数值型

1
2
3
4
5
6
numeric_strings = np.array(['1.2','2.3','3.2141'], dtype=np.string_)
numeric_strings
	array(['1.2', '2.3', '3.2141'], dtype='|S6')
// 此处写的是float 而不是np.float64, Numpy很聪明，会将python类型映射到等价的dtype上
numeric_strings.astype(float)
	array([ 1.2, 2.3, 3.2141])

C

python numpy copy 函数

讲解原文

numpy关于copy有三种情况，完全不复制、视图（view）或者叫浅复制（shadow copy）和深复制（deep copy）。

而 b = a[:] 这种形式就属于第二种，即视图，这本质上是一种切片操作（slicing），所有的切片操作返回的都是视图。具体来说，b = a[:]会创建一个新的对象 b（所以 id(b) 和id(a) 返回的结果是不一样的），但是 b 的数据完全来自于a，和 a 保持完全一致，换句话说，b的数据完全由a保管，他们两个的数据变化是一致的，可以看下面的示例:

1
2
3
4
5
6
7
8
9
10
a = np.arange(4)  # array([0, 1, 2, 3])
b = a[:]  # array([0, 1, 2, 3])
b.flags.owndata  # 返回 False，b 并不保管数据
a.flags.owndata  # 返回 True，数据由 a 保管
# 改变 a 同时也影响到 b
a[-1] = 10  # array([0, 1, 2, 10])
b  #  array([0, 1, 2, 10])
# 改变 b 同时也影响到 a
b[0] = 10  # array([10, 1, 2, 10])
a  # array([10, 1, 2, 10])

b = a 和 b = a[:] 的差别就在于后者会创建新的对象，前者不会。两种方式都会导致 a 和 b 的数据相互影响。
要想不让 a 的改动影响到 b，可以使用深复制：

1
unique_b = a.copy()

有一点需要特别注意，numpy 的复制 和 python 的 list 复制是不一样的

1
2
3
4
5
6
7
8
9
10
11
import numpy as np
a = [1,2,3,4]
b = a[:]
a[1] = 10
print(b)
	[1,2,3,4]
a = np.arange(4)
b = a[:]
a[1] = 10
print(b)
	[0,10,2,3]

D

diff()

numpy.diff(a, n=1,axis=-1)

沿着指定轴计算第N维的离散差值

参数：

  • a：输入矩阵
  • n：可选，代表要执行几次差值
  • axis：默认是最后一个 
1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np

A = np.arange(2 , 14).reshape((3 , 4))
A[1 , 1] = 8
print('A:' , A)
	# A: [[ 2  3  4  5]
	#  [ 6  8  8  9]
	#  [10 11 12 13]]

print(np.diff(A))
	# [[1 1 1]
	#  [2 0 1]
	#  [1 1 1]]

从输出结果可以看出，其实diff函数就是执行的是后一个元素减去前一个元素。

python numpy dot 函数

dot()函数是矩阵乘，而*则表示逐个元素相乘

dot()函数可以通过numpy库调用，也可以由数组实例对象进行调用。a.dot(b) 与 np.dot(a,b)效果相同

矩阵积计算不遵循交换律,np.dot(a,b) 和 np.dot(b,a) 得到的结果是不一样的。

而且，这个函数处理一维和多维的结果也是不一样的。

处理一维得到的是两数组的內积

1
2
3
4
5
6
a = np.arange(5)
b = a[::-1]
print(np.dot(a,b))
	10
print(np.dot(b,a))
	10

如果是二维数组（矩阵）之间的运算，则得到的是矩阵积

1
2
3
4
5
a = np.arange(1,5).reshape(2,2)
b = np.arange(5,9).reshape(2,2)
print(np.dot(a,b))
	[[19 22]
	[43 50]]

这是将二进制翻译成十进制，装逼必备代码

1
pop.dot(2 ** np.arange(DNA_SIZE)[::-1])

F

python numpy fromstring 函数

使用字符串创建矩阵,将 python 中的字符串，转化为 numpy 中指定类型的矩阵

1
2
3
4
import numpy as np
s = np.fromstring("licong",dtype=np.uint8)
print(s)
	# [108 105  99 111 110 103] 里面的数字代表的是字母的 ASCII 码

H

hstack()

hstack(tup) ，参数tup可以是元组，列表，或者numpy数组，返回结果为numpy的数组。

对于这个函数我是这样理解的，这个函数会让不同变量下的相同地位的数据放在一个维度下，并且优先按照行排列。

比如第一个代码，两个数据都是一维，所以，他们里面的数据处于同等地位，按照行排列，最后输出。

1
2
3
4
5
6
import numpy as np
a=[1,2,3]
b=[4,5,6]
print(np.hstack((a,b)))

输出：[1 2 3 4 5 6 ]

下面的代码中，每个变量都有三个维度的数据，他们相同下标下对应的维度是相同，优先按照行排列，最后输出。

1
2
3
4
5
6
7
8
9
import numpy as np
a=[[1],[2],[3]]
b=[[6],[7],[8]]
c=[[9],[10],[11]]
d=[[1],[2],[3]]
print(np.hstack((a,b,c,d)))
	#[[ 1  6  9  1]
		[ 2  7 10  2]
		[ 3  8 11  3]]

E

empty()

numpy.empty(shape, dtype=float, order=’C’)

shape：int或int类型元组，表示矩阵形状
dtype：输出的数据类型
order：‘C’ 或者 ‘F’，表示数组在内存的存放次序是以行(C)为主还是以列(F)为主

返回生成随机矩阵

1
2
3
4
5
6
np.empty([2, 2])
	# array([[ -9.74499359e+001,   6.69583040e-309],
		[  2.13182611e-314,   3.06959433e-309]])         #random
np.empty([2, 2], dtype=int)
	# array([[-1073741821, -1067949133],
		[  496041986,    19249760]])                     #random

empty_like()

numpy.empty_like(a, dtype=None, order=’K’, subok=True)

a：返回值仿照的矩阵
dtype：输出的数据类型
order：‘C’ 、 ‘F’、 ‘A’、 ‘K’，表示数组在内存的存放次序是以行(C)为主还是以列(F)为主，‘A’表示以列为主存储，如果a是列相邻的，‘K’表示尽可能与a的存储方式相同
subok：bool类型，True：使用a的内部数据类型，False：使用a数组的数据类型

返回值是生成与a相似（形态和数据类型）的随机矩阵

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
import numpy as np
a = ([1,2,3],[4,5,6])
print(a)
	# ([1, 2, 3], [4, 5, 6])
print(type(a))
	# <class 'tuple'>
print(np.empty_like(a))
	# [[1702060387  543584032 1818845542]
		[ 778400373  538976266 1919252000]]
b = [[1,2,3],[4,5,6]]
print(b)
	# [[1, 2, 3], [4, 5, 6]]
print(type(b))
	# <class 'list'>
print(np.empty_like(b))
	# [[1 2 3]
		[4 5 6]]

L

python numpy linspace

numpy.linspace是用于创建一个一维数组，并且是等差数列构成的一维数组，它最常用的有三个参数。当然它不只有三个参数，我们通过例子来了解它是如何使用的：

我们看一下第一个例子，用到三个参数，第一个参数表示起始点，第二个参数表示终止点，第三个参数表示数列的个数。

特别注意的是：

numpy.arange()，该函数返回的是一个均匀分布的数组，step一般为整数，如果需要步长不为整数的情况，可以使用linspace
1
2
a = np.linspace(1,10,10)
	# array([  1.,   2.,   3.,   4.,   5.,   6.,   7.,   8.,   9.,  10.])

用它创建一个元素全部是1的等差数列，或者你也可以让所有的元素为0。

1
2
a = np.linspace(1,1,10)
	# array([ 1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.,  1.])

linspace创建的数组元素的数据格式，当然是浮点型

1
2
a.dtype
	# dtype('float64')

还可以使用参数endpoint来决定是否包含终止值，如果不设置这个参数，默认是True

1
2
a = np.linspace(1,10,10,endpoint=False)
	# array([ 1. ,  1.9,  2.8,  3.7,  4.6,  5.5,  6.4,  7.3,  8.2,  9.1])

装逼代码必备

1
2
3
4
5
import numpy as np
import matplotlib.pyplot as plt
a = [1,5]
print(np.linspace(*a,10))
	# 上面的代码相当于 print(np.linspace(a[0],a[1],10))

loadtxt()

loadtxt(fname, dtype=<class ‘float’>, comments=’#’, delimiter=None, converters=None, skiprows=0, usecols=None, unpack=False, ndmin=0)

fname要读取的文件、文件名、或生成器。
dtype数据类型，默认float。
comments注释。
delimiter分隔符，默认是空格。
skiprows跳过前几行读取，默认是0，必须是int整型。
usecols：要读取哪些列，0是第一列。例如，usecols = （1,4,5）将提取第2，第5和第6列。默认读取所有列。
unpack如果为True，将分列读取。

python numpy linalg模块

NumPy 包包含numpy.linalg模块，提供线性代数所需的所有功能。

numpy.linalg.det()

行列式在线性代数中是非常有用的值。 它从方阵的对角元素计算。 对于 2×2 矩阵，它是左上和右下元素的乘积与其他两个的乘积的差。

换句话说，对于矩阵[[a，b]，[c，d]]，行列式计算为ad-bc。 较大的方阵被认为是 2×2 矩阵的组合。

numpy.linalg.det()函数计算输入矩阵的行列式。

1
2
3
4
import numpy as np
a = np.array([[1,2], [3,4]]) 
print np.linalg.det(a)
	# -2.0

所以可以用这个函数判断一下是否可逆：

1
2
3
if np.linalg.det(xTx) == 0.0:
    print('不可逆')
    return

numpy.linalg.inv()

我们使用numpy.linalg.inv()函数来计算矩阵的逆。但是我们有更简单的方法，如 A.I 就是求逆。

关于求逆的细节，可以参考我的博文。

论numpy中matrix 和 array的区别

numpy.linalg.solve()

numpy.linalg.solve()函数给出了矩阵形式的线性方程的解。

考虑以下线性方程：

x + y + z = 6
2y + 5z = -4
2x + 5y - z = 27

可以使用矩阵表示为：

如果矩阵成为A、X和B，方程变为：

AX = B

或

X = A^(-1)B

举一个例子：

1
2
3
ws = X.I * (xMat.T * yMat)
# 可以换成下面这个：
ws = np.linalg.solve(X,xMat.T * yMat)

M

python numpy mat

mat函数可以将目标数据的类型转换为矩阵（matrix）， 因此可以使用mat函数将一个列表a转换成相应的矩阵类型。

1
2
3
4
5
6
7
8
9
10
import numpy as np
a=[[1,2,3,],
     [3,2,1]]
type(a)
	#list
myMat=np.mat(a)
myMat
	#matrix([[1,2,3],[3,2,1]])
type(myMat)
	#numpy.matrixlib.defmatrix.martix

max()

直接上代码

1
2
3
4
5
6
7
8
9
10
import numpy as np
data = np.arange(0,12,1).reshape(3,4)
print(data)
	# [[ 0  1  2  3]
	#[ 4  5  6  7]
	#[ 8  9 10 11]]
print(np.max(data,1))
	# [ 3  7 11]
print(np.max(data,0))	
	# [ 8  9 10 11]

python numpy mean

计算矩阵的均值

1
2
3
4
5
6
7
a = np.array([[1, 2], [3, 4]])  
np.mean(a) # 将上面二维矩阵的每个元素相加除以元素个数（求平均数）  
	# 2.5  
np.mean(a, axis=0) # axis=0，计算每一列的均值  
	# array([ 2.,  3.])  
np.mean(a, axis=1) # 计算每一行的均值  
	# array([ 1.5,  3.5])

N

newaxis

numpy中包含的newaxis可以给原数组增加一个维度

np.newaxis放的位置不同，产生的新数组也不同

一维数组

x = np.random.randint(1, 8, size=5)
x
    Out[48]: array([4, 6, 6, 6, 5])
x1 = x[np.newaxis, :]
x1
    Out[50]: array([[4, 6, 6, 6, 5]])
x2 = x[:, np.newaxis]
x2
    Out[52]: 
    array([[4],
           [6],
           [6],
           [6],
           [5]])

由以上代码可以看出，当把newaxis放在前面的时候

以前的shape是5，现在变成了1××5，也就是前面的维数发生了变化，后面的维数发生了变化

而把newaxis放后面的时候，输出的新数组的shape就是5××1，也就是后面增加了一个维数

所以，newaxis放在第几个位置，就会在shape里面看到相应的位置增加了一个维数

如下：

这个操作可是很重要，如果是 100 * 100 的 shape

将数据这样

data[:,:,np.newaxis]

最后 shape 就变成了 100 * 100 * 1 了

一般问题

经常会遇到这样的问题，需要从数组中取出一部分的数据，也就是取出“一片”或者“一条”

比如需要从二维数组里面抽取一列

取出来之后维度却变成了一维

假如我们需要将其还原为二维，就需要上面的方法了

R

random 板块

python random.choice

numpy.random.choice(a,size=None,replace=True,p=None)

若a为数组，则从a中选取元素；若a为单个int类型数，则选取range(a)中的数

replace是bool类型，为True，则选取的元素会出现重复；反之不会出现重复

p为数组，里面存放选到每个数的可能性，即概率，值得注意的是 p 中的概率之和是 1

1
2
print(np.random.choice(5,size=4,replace=True,p=[0.1,0.1,0.2,0.5,0.1]))
	#	[2 3 3 3]

python random.normal

np.random.normal()的意思是一个正态分布，normal这里是正态的意思。我在看孪生网络的时候看到这样的一个例子：numpy.random.normal(loc=0,scale=1e-2,size=shape) ，意义如下： 

参数loc(float)：正态分布的均值，对应着这个分布的中心。loc=0说明这一个以Y轴为对称轴的正态分布，
参数scale(float)：正态分布的标准差，对应分布的宽度，scale越大，正态分布的曲线越矮胖，scale越小，曲线越高瘦。
参数size(int 或者整数元组)：输出的值赋在shape里，默认为None。

python random.rand

numpy.random.rand(d0,d1,…dn)

以给定的形状创建一个数组，并在数组中加入在[0,1]之间均匀分布的随机样本。 

1
2
3
print(np.random.rand(2,3))
	[[0.14132485 0.56433519 0.8146228 ]
	[0.332916   0.88956782 0.61115085]]

python random.randn

numpy.random.rand(d0,d1,…dn)

以给定的形状创建一个数组，数组元素来符合标准正态分布N(0,1)

N(μ,σ^2)

1
2
3
print(np.random.randn(2,3))
	[ 0.82942049 -1.21329075  2.37576017]
	[-1.28842471 -0.88193488 -0.37684046]]

python random.randint

numpy.random.randint(low,high=None,size=None,dtype)

生成在半开半闭区间[low,high)上离散均匀分布的整数值;若high=None，则取值区间变为[0,low)

在统计学及概率理论中，离散型均匀分布是一个离散型概率分布，其中有限个数值拥有相同的概率。

1
2
3
print(np.random.randint(2,10,size=(2,3)))
	[[8 4 5]
	[7 8 9]]

python random.permutation()

shuffle 的参数只能是 array_like，而 permutation 除了 array_like 还可以是 int 类型，如果是 int 类型，那就随机打乱 numpy.arange(int)。

shuffle 返回 None，这点尤其要注意，也就是说没有返回值，而 permutation 则返回打乱后的 array。

permutation 其实在内部实现也是调用的 shuffle，这点从 Numpy 的源码 可以看出来：

1
2
3
4
5
6
7
8
def permutation(self, object x):
    '''这里都是帮助文档，我就省略了'''
    if isinstance(x, (int, long, np.integer)):
        arr = np.arange(x)
    else:
        arr = np.array(x)
    self.shuffle(arr)
    return arr
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np
a = np.arange(0,12).reshape(3,4)
print(a)
	# [[ 0  1  2  3]
		[ 4  5  6  7]
		[ 8  9 10 11]]
b = a.copy()
print(b)
	# [[ 0  1  2  3]
		[ 4  5  6  7]
		[ 8  9 10 11]]
np.random.shuffle(a)
print("shuffle")
print(a)
	# [[ 4  5  6  7]
		[ 8  9 10 11]
		[ 0  1  2  3]]
print("permutation")
print(np.random.permutation(b))
	# [[ 0  1  2  3]
		[ 4  5  6  7]
		[ 8  9 10 11]]

python random.shuffle()

只是对一个矩阵进行洗牌，无返回值。

速度比较：

可以看出在达到 109109 级别以前，两者速度几乎没有差别，但是在 达到 109109 以后两者速度差距明显拉大，shuffle 的用时明显短于 permutation。

所以在 array 很大的时候还是使用 shuffle 速度更快些，但要注意其不返回打乱后的 array，是 inplace 修改。

repeat()

repeat函数的作用： 扩充数组元素或降低数组维度

numpy.repeat(a, repeats, axis=None)：若axis=None，对于多维数组而言，可以将多维数组变化为一维数组，然后再根据repeats参数扩充数组元素；若axis=M，表示数组在轴M上扩充数组元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np

arr = np.arange(12).reshape(1,4,3)
# 上面的语句换为
# arr = np.arange(12).reshape(4,3)
# 最后的结果也是一样的，因为 repeat 之后，就变成 1 * n 的数组了
print(arr)
    # [[[ 0  1  2]
    #   [ 3  4  5]
    #   [ 6  7  8]
    #   [ 9 10 11]]]

print(arr.repeat(1))
    # [ 0  1  2  3  4  5  6  7  8  9 10 11]
print(arr.repeat(2))
    # [ 0  0  1  1  2  2  3  3  4  4  5  5  6  6  7  7  8  8  9  9 10 10 11 11]
    # 降维后，每个元素的个数变为 2
# 如参数是一维数
print(arr.repeat([2]))
    # [ 0  0  1  1  2  2  3  3  4  4  5  5  6  6  7  7  8  8  9  9 10 10 11 11]
# 如果参数是多维数组，则维数必须和对应的改变的维数相同，并且，增加的次数和多维数组的数对应
# 如果两者的维数不同，则会出错
# 在这里要注意的是我们的多维数组应该和降维后的数组维数对应
a = np.ones((12),dtype=np.int8)
a[0] = 3
print(a)
    # [3 1 1 1 1 1 1 1 1 1 1 1]
print(arr.repeat(a))
    # [ 0  0  0  1  2  3  4  5  6  7  8  9 10 11]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import numpy as np

arr = np.arange(12).reshape(2,2,3)
print(arr)
    # [[[0  1  2]
    #   [3  4  5]]
    #
    # [[ 6  7  8]
    #   [ 9 10 11]]]
# 我认为 axis 就是表示在第几层，最外层是 0，向里依次增加。
# 但是有一点要注意的是最外层的[] 不算
# 其实我也将不太清楚，所以直接看例子就好
print(arr.repeat((1,2),axis = 0))
    # [[[ 0  1  2]
    #   [ 3  4  5]]
    #
    #  [[ 6  7  8]
    #   [ 9 10 11]]
    #
    #  [[ 6  7  8]
    #   [ 9 10 11]]]

print(arr.repeat((1,2),axis = 1))
    # [[[ 0  1  2]
    #   [ 3  4  5]
    #   [ 3  4  5]]
    #
    #  [[ 6  7  8]
    #   [ 9 10 11]
    #   [ 9 10 11]]]

print(arr.repeat((1,2),axis = 2))
    # 出错

reshape()

numpy.reshape(a, newshape, order=’C’)中的newshape参数和order参数。

两种表达形式

1
2
3
a=np.array([1,2,3,4,5,6,7,8,9,10,11,12])
b=np.reshape(a,(2,-1))
c=a.reshape(2,-1)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
import numpy as np

arr = np.arange(12).reshape(4,3)
print(arr)
    # [[ 0  1  2]
    #  [ 3  4  5]
    #  [ 6  7  8]
    #  [ 9 10 11]]
arr = np.arange(12).reshape(1,4,3)
print(arr)
    # [[[ 0  1  2]
    #   [ 3  4  5]
    #   [ 6  7  8]
    #   [ 9 10 11]]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
import numpy as np
 
a=np.array([1,2,3,4,5,6,7,8,9,10,11,12])
b=np.reshape(a,(2,-1))
	#	b=
		[[ 1  2  3  4  5  6]
		[ 7  8  9 10 11 12]]
c=np.reshape(a,(2,2,-1))
	#	
		[[[ 1  2  3]
		[ 4  5  6]]
 
		[[ 7  8  9]
		[10 11 12]]]
d=np.reshape(a,(2,3,-1))
	#	
		[[[ 1  2]
		[ 3  4]
		[ 5  6]]
 
		[[ 7  8]
		[ 9 10]
		[11 12]]]

newshape参数用数组表示，以c为例，数组(2,2,-1)就是c的形状，一共有三阶，第三个数字是reshape后数组a中最小单元中元素个数，在这里是3，如果是-1则表示可以自动推测出。

S

seterr

这个函数是可以让错误出不出现

numpy.seterr(all=None, divide=None, over=None, under=None, invalid=None)

Set how floating-point errors are handled.

all : {‘ignore’, ‘warn’, ‘raise’, ‘call’, ‘print’, ‘log’}, optional
    Set treatment for all types of floating-point errors at once:
        ignore: Take no action when the exception occurs.
        warn: Print a RuntimeWarning (via the Python warnings module).
        raise: Raise a FloatingPointError.
        call: Call a function specified using the seterrcall function.
        print: Print a warning directly to stdout.
        log: Record error in a Log object specified by seterrcall.
        The default is not to change the current behavior.
divide : {‘ignore’, ‘warn’, ‘raise’, ‘call’, ‘print’, ‘log’}, optional
Treatment for division by zero.
over : {‘ignore’, ‘warn’, ‘raise’, ‘call’, ‘print’, ‘log’}, optional
Treatment for floating-point overflow.
under : {‘ignore’, ‘warn’, ‘raise’, ‘call’, ‘print’, ‘log’}, optional
Treatment for floating-point underflow.
invalid : {‘ignore’, ‘warn’, ‘raise’, ‘call’, ‘print’, ‘log’}, optional
Treatment for invalid floating-point operation.

return

old_settings : dict
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
import numpy as np
np.seterr(all='ignore')
a = np.arange(0,10,1)
b = 0
c = a / b
print(c)
	# [nan inf inf inf inf inf inf inf inf inf]
	
import numpy as np
a = np.arange(0,10,1)
b = 0
c = a / b
print(c)
	# E:\code\别人的代码\EEG\MUSE-EEG-Classification\test\test.py:4: RuntimeWarning: divide by zero encountered in true_divide
		#[nan inf inf inf inf inf inf inf inf inf]
		#c = a / b
		#E:\code\别人的代码\EEG\MUSE-EEG-Classification\test\test.py:4: RuntimeWarning: invalid value encountered in true_divide
		#c = a / b

python numpy shape

shape函数是numpy.core.fromnumeric中的函数，它的功能是查看矩阵或者数组的维数。

1
2
3
4
5
6
7
8
import numpy as np
data = np.array([[2,4,3],[4,6,5]])
print(data.shape)
	# (2, 3)
print(data.shape[0])
	# 2
print(data.shape[1])
	# 3

python numpy sum 函数用法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
import numpy as np
data = np.array([[1,2],[2,2]]);
print(np.sum(data));
	# 7 全加
print(np.sum(data,axis=0));
	#[3 4]
print(np.sum(data,axis=1));
	#[3 4]
import numpy as np
a = np.arange(1,10)
b = np.arange(1,10)
b[2] = 6
print(a == b)
	# [ True  True False  True  True  True  True  True  True] 是一个向量
print((a == b).shape)
	# (9,)
print((a == b).reshape(1,9))
	# [[ True  True False  True  True  True  True  True  True]]
print((a == b).reshape(1,9).shape)
	# (1, 9)
print((a == b).sum(axis=0))
	# axis 为 0 的时候，是列相加
	# 8
print((a == b).reshape(1,9).sum(axis=1))
	# axis 为 1 的时候，是行相加
	# [8]

对于多维数组

1
2
3
4
5
6
7
8
9
10
11
 
import numpy as np
a = np.arange(12).reshape((3,4))
print(a)
	# [[ 0  1  2  3]
		[ 4  5  6  7]
		[ 8  9 10 11]]
print(a.sum(axis=0)) # 为 0 的时候，表示列相加
	# [12 15 18 21]
print(a.sum(axis = 1))	# 为 1 的时候，表示行相加
	# [ 6 22 38]

python numpy sorted 函数用法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
这个方法我在用numpy实际操作的时候，发现没有，但是查阅相关文档，貌似又有，可能是版本问题。但是这个方法是python自带的。

sorted(data, cmp=None, key=None, reverse=False)  
		#data是待排序数据，可以使List或者iterator, cmp和key都是函数，这两个函数作用与data的元素上产生一个结果，sorted方法根据这个结果来排序。 
		#cmp(e1, e2) 是带两个参数的比较函数, 返回值: 负数: e1 < e2, 0: e1 == e2, 正数: e1 > e2. 默认为 None, 即用内建的比较函数. 
		#key 是带一个参数的函数, 用来为每个元素提取比较值. 默认为 None, 即直接比较每个元素. 
		#通常, key 和 reverse 比 cmp 快很多, 因为对每个元素它们只处理一次; 而 cmp 会处理多次. 
	1. 对由tuple组成的List排序 
	students = [('john', 'A', 15), ('jane', 'B', 12), ('dave', 'B', 10),]  

	用key函数排序
	sorted(students, key=lambda student : student[2])   # sort by age  
	[('dave', 'B', 10), ('jane', 'B', 12), ('john', 'A', 15)]  
	
	用 operator 函数来加快速度, 上面排序等价于
	from operator import itemgetter, attrgetter  
	sorted(students, key=itemgetter(2))  
	
	2. 对由字典排序 
	d = {'data1':3, 'data2':1, 'data3':2, 'data4':4}  
	sorted(d.iteritems(), key=itemgetter(1), reverse=True)  
	[('data4', 4), ('data1', 3), ('data3', 2), ('data2', 1)]

stack()

stack(arrays, axis=0)，arrays可以传数组和列表。

对arrays里面的每个元素变成numpy的数组后，再对每个元素增加一维，然后再把这些元素串起来。

这个理解有点复杂，但是只是 axis 为 0 和 1 的话，很容易理解，如果再高就比较难理解了，但是还是把代码贴出来。

原文

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
import numpy as np
a=[[1,2,3],
   [4,5,6]]
   
print(a)
	# [[1, 2, 3], [4, 5, 6]]

	# 增加一维，新维度的下标为0
c=np.stack(a,axis=0)
print(c)
	# [[1 2 3]
		[4 5 6]]

	# 增加一维，新维度的下标为1
c=np.stack(a,axis=1)
print(c)
	# [[1 4]
		[2 5]
		[3 6]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
import numpy as np
a=[[1,2,3,4],
   [5,6,7,8],
   [9,10,11,12]]
print("列表a如下：")
print(a)

print("增加一维，新维度的下标为0")
c=np.stack(a,axis=0)
print(c)

print("增加一维，新维度的下标为1")
c=np.stack(a,axis=1)
print(c)

输出：
列表a如下：
[[1, 2, 3, 4], [5, 6, 7, 8], [9, 10, 11, 12]]
增加一维，新维度的下标为0
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
增加一维，新维度的下标为1
[[ 1  5  9]
 [ 2  6 10]
 [ 3  7 11]
 [ 4  8 12]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
import numpy as np
a=[1,2,3,4]
b=[5,6,7,8]
c=[9,10,11,12]
print("a=",a)
print("b=",b)
print("c=",c)

print("增加一维，新维度的下标为0")
d=np.stack((a,b,c),axis=0)
print(d)

print("增加一维，新维度的下标为1")
d=np.stack((a,b,c),axis=1)
print(d)

输出：
('a=', [1, 2, 3, 4])
('b=', [5, 6, 7, 8])
('c=', [9, 10, 11, 12])
增加一维，新维度的下标为0
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
增加一维，新维度的下标为1
[[ 1  5  9]
 [ 2  6 10]
 [ 3  7 11]
 [ 4  8 12]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
import numpy as np
a=[[1,2,3],
   [4,5,6]]
b=[[1,2,3],
   [4,5,6]]
c=[[1,2,3],
   [4,5,6]]
print("a=",a)
print("b=",b)
print("c=",c)

print("增加一维，新维度的下标为0")
d=np.stack((a,b,c),axis=0)
print(d)

print("增加一维，新维度的下标为1")
d=np.stack((a,b,c),axis=1)
print(d)
print("增加一维，新维度的下标为2")
d=np.stack((a,b,c),axis=2)
print(d)

输出：
('a=', [[1, 2, 3], [4, 5, 6]])
('b=', [[1, 2, 3], [4, 5, 6]])
('c=', [[1, 2, 3], [4, 5, 6]])
增加一维，新维度的下标为0
[[[1 2 3]
  [4 5 6]]

 [[1 2 3]
  [4 5 6]]

 [[1 2 3]
  [4 5 6]]]
增加一维，新维度的下标为1
[[[1 2 3]
  [1 2 3]
  [1 2 3]]

 [[4 5 6]
  [4 5 6]
  [4 5 6]]]
增加一维，新维度的下标为2
[[[1 1 1]
  [2 2 2]
  [3 3 3]]

 [[4 4 4]
  [5 5 5]
  [6 6 6]]]

std()

计算矩阵标准差

标准差是衡量观测值相对平均值的分散程度。较大的标准差，说明观测数组的相对均值的波动比较大。

如果观测值是总体，标准差根号内除以n，如果是样本，标准差公式根号内除以n-1，因为我们大量接触的是样本所以基本都是除以n-1，除以的这个数字又叫做自由度。

numpy.std() 求标准差的时候默认是除以 n 的，即是有偏的，np.std无偏样本标准差方式为 ddof = 1；

pandas.std() 默认是除以n-1 的，即是无偏的，如果想和numpy.std() 一样有偏，需要加上参数ddof=0 ，即pandas.std(ddof=0) ；DataFrame的describe()中就包含有std()；

numpy.std(a, axis=None, dtype=None, out=None, ddof=0, keepdims=)

a : array_like 
    计算的数据
axis : None or int or tuple of ints, optional 
    默认是计算平铺的数组，可以选择计算的方向
dtype : dtype, optional 
    调节计算的精度
out : ndarray, optional 
    输出选择
ddof : int, optional 
    控制自由度，自由度=N - ddof，N是数据的长度。当ddof=1时，就是样本标准差，当ddof=0时，是总体标准差
keepdims : bool, optional
1
2
3
4
5
6
7
a = np.array([[1, 2], [3, 4]])
np.std(a) # 计算全局标准差
	# 1.1180339887498949
np.std(a, axis=0) # axis=0计算每一列的标准差
	# array([ 1.,  1.])
np.std(a, axis=1) # 计算每一行的标准差
	# array([ 0.5,  0.5])

T

tolist()

将 numpy 的数据转化为 python 的 list

1
2
3
4
5
6
7
a = np.arange(1,10)
print(a.dtype)
	# int32
print(type(a.tolist()))
	# <class 'list'>
print(a.tolist().dtype)
	# AttributeError: 'list' object has no attribute 'dtype'

python numpy tostring函数

将 numpy 的字符串转化为 python 的字符串

将 numpy 的字符串转化为 python 的字符串

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
s = np.fromstring("licong",dtype=np.uint8)
print(s)
	# [108 105  99 111 110 103]
print(type(s))
	# <class 'numpy.ndarray'>
print(s.tostring())
	# b'licong'
print(type(s.tostring()))
	# <class 'bytes'>
print(s.tostring().decode('ascii'))
	# licong

python numpy tile函数用法

tile函数位于python模块 numpy.lib.shape_base中，他的功能是重复某个数组。比如tile(A,n)，功能是将数组A重复n次，构成一个新的数组，我们还是使用具体的例子来说明问题:

1
2
3
4
5
6
7
8
9
10
11
12
import numpy as np
data = np.array([[1,2]])
print(np.tile(data,(1,1)));
	[[1 2]]
print(np.tile(data,(2,1)));
	[[1 2]
	[1 2]]
print(np.tile(data,(2,2)));
	[[1 2 1 2]
	[1 2 1 2]]
print(np.tile(data,(1,2)));
	[[1 2 1 2]]

V

python numpy var

表示方差

要注意上面式子描述的平均值是 μ ，所以下面除以 N ，而不是 N - 1，关于这个疑问，请参考我的博文。

为什么样本方差（sample variance）的分母是 n-1？

1
2
3
4
5
6
7
8
import numpy as np
data = np.array([[1,2,3],[5,9,15]])
A = np.var(data)
	# 23.472222222222225
B = np.var(data,axis=0) # 列的方差
	# [ 4.   12.25 36.  ]
C = np.var(data,axis=1) # 行的方差
	# [ 0.66666667 16.88888889]

vstack()

vstack(tup) ，参数tup可以是元组，列表，或者numpy数组，返回结果为numpy的数组。

对于这个函数我是这样理解的，这个函数让不同变量下的数据按照维度采用列排列。

对于下面的代码，a 和 b 中的数据都是一个维度，所以输出如下。

1
2
3
4
5
6
7
8
import numpy as np
a=[1,2,3]
b=[4,5,6]
print(np.vstack((a,b)))

输出：
[[1 2 3]
 [4 5 6]]

下面的代码中，每个变量中的数据都有自己的维度，先排 a 的，然后依次排下去，最后输出。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

import numpy as np
a=[[1],[2],[3]]
b=[[6],[7],[8]]
c=[[9],[10],[11]]
d=[[1],[2],[3]]
print(np.vstack((a,b,c,d)))
	# [[ 1]
		[ 2]
		[ 3]
		[ 6]
		[ 7]
		[ 8]
		[ 9]
		[10]
		[11]
		[ 1]
		[ 2]
		[ 3]]
请我喝杯咖啡吧～